Crypto-对称密码(一)

angelkat

已于 2024-01-19 15:53:13 修改

阅读量647

点赞数 7

分类专栏： crypto 文章标签：密码学

于 2024-01-19 15:49:49 首次发布

本文链接：https://blog.csdn.net/lastwinn/article/details/135699837

版权

crypto 专栏收录该内容

3 篇文章 2 订阅

订阅专栏

对称密码概述

对称密码：其实就是使用同一种密钥进行加密解密。

question : 非对称密码是对称密码之后提出来的，我们知道非对称密码比对称密码安全，那么为什么还要用对称密码呢?

answer：对称密码的计算速度比非对称密码快多了，非对称密码考虑的东西比较多，例如密钥过长、算法较复杂、需要分块填充算法等等。

大部分 对称密码都是基于加法（ADD）、移位（Rotate）、异或（Xor）。简称ARX操作。 非对称密码会有很多像幂运算、指数运算等等需要算力的的操作。

Des加密

Des是一种典型的块加密，什么是块加密呢，就是将明文分为一块一块的，分别对明文的每一块进行加密，然后拼接得到密文。
Des的特点
- 输入的是64位
- 输出的是64位
- 密钥是64位，使用的密钥中的56位是用来加密的，后8位是作为奇偶校验位，或者丢弃掉。
- 采用Feistel迭代结构
  - 明文经过16轮迭代得到密文
  - 密文经过类似的16轮迭代得到明文

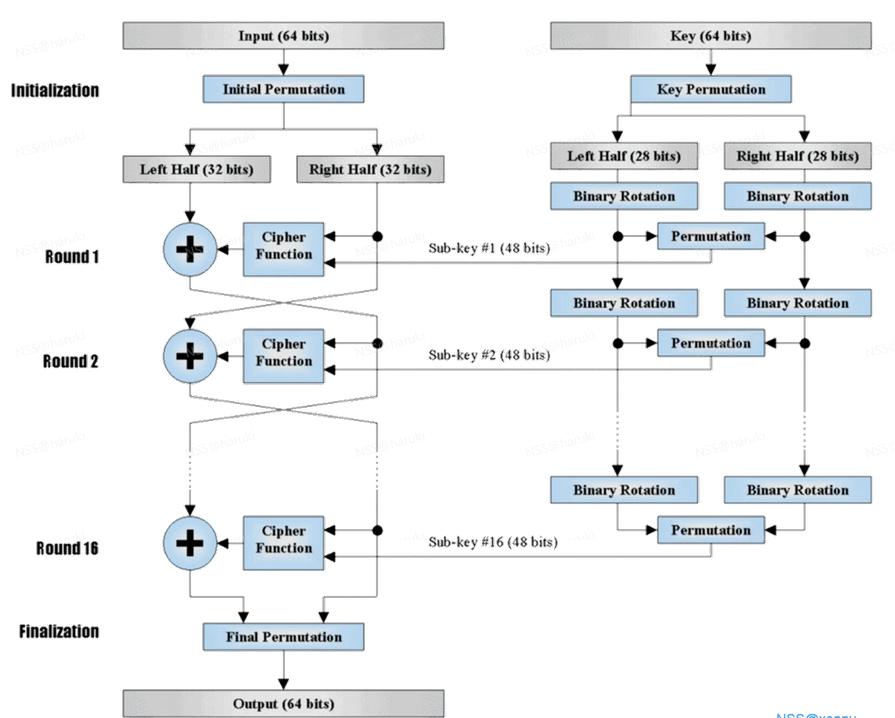
明文初始置换

64位的明文分组x经过一个初始置换函数，函数名称叫做IP，通过该函数生成64位的x0,分为前半部分和后半部分，分别是L0和R0。
- 将第58位换到第1位，第50位换到第2位…以此类推。
- 得到的结果是前面32位为L0，后面32位为R0。

 1, 2, 3, 4, 5, 6, 7, 8
 9,10,11,12,13,14,15,16
17,18,19,20,21,22,23,24
25,26,27,28,29,30,31,32
33,34,35,36,37,38,39,40
41,42,43,44,45,46,47,48
49,50,51,52,53,54,55,56
57,58,59,60,61,62,63,64
得到结果
58,50,42,34,26,18,10,2
60,52,44,36,28,20,12,4
62,54,46,38,30,22,14,6
64,56,48,40,32,24,16,8
57,49,41,33,25,17,9 ,1
59,51,43,35,27,19,11,3
61,53,45,37,29,21,13,5
63,55,47,39,31,23,15,7

那么我们可以构造一个IP函数，python代码如下：

_IP = [57, 49, 41, 33, 25, 17, 9,  1,
	59, 51, 43, 35, 27, 19, 11, 3,
	61, 53, 45, 37, 29, 21, 13, 5,
	63, 55, 47, 39, 31, 23, 15, 7,
	56, 48, 40, 32, 24, 16, 8,  0,
	58, 50, 42, 34, 26, 18, 10, 2,
	60, 52, 44, 36, 28, 20, 12, 4,
	62, 54, 46, 38, 30, 22, 14, 6
]

def IP(plain: List[int]):
    return list(map(lambda x: plain[x], _IP))

为什么每个都减1呢，那是因为数组下标从0开始的。

获取子密钥

在进行第一轮加密之前，我们还需要通过密钥生成16轮的子密钥，之前讲了参与运算的密钥长度只有56位，后8位为奇偶校验，那么如何生成呢？
- 1、将64位密钥去掉8个校验位，用56位密钥[7*8]按照如下表格进行置换。
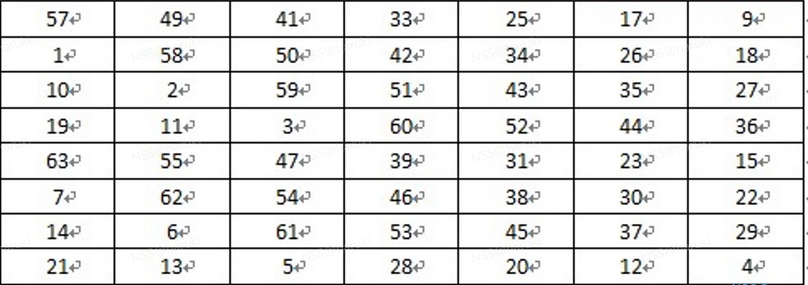
- 2、置换的结果也是[7*8],那么取前28位为C0，后28位为D0。
- 3、需要分别对C0,D0进行循环移位（例如：123456移位得到234561）。移位的次数是一次或者两次，移动多少次跟轮次有关系，轮次关系如下图：
- 4、移动后，将C0和D0进行合并，然后通过置换得到48位子密钥(去掉了8个)，置换表格如下：
  
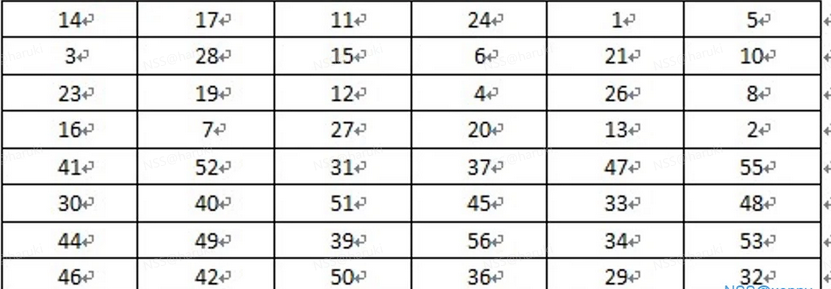
  实现代码如下：

__pc1 = [56, 48, 40, 32, 24, 16,  8,
	  0, 57, 49, 41, 33, 25, 17,
	  9,  1, 58, 50, 42, 34, 26,
	 18, 10,  2, 59, 51, 43, 35,
	 62, 54, 46, 38, 30, 22, 14,
	  6, 61, 53, 45, 37, 29, 21,
	 13,  5, 60, 52, 44, 36, 28,
	 20, 12,  4, 27, 19, 11,  3
]

__pc2 = [
	13, 16, 10, 23,  0,  4,
	 2, 27, 14,  5, 20,  9,
	22, 18, 11,  3, 25,  7,
	15,  6, 26, 19, 12,  1,
	40, 51, 30, 36, 46, 54,
	29, 39, 50, 44, 32, 47,
	43, 48, 38, 55, 33, 52,
	45, 41, 49, 35, 28, 31
]
ROTATIONS = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]

def PC_1(key: List[int]):
    return list(map(lambda x: key[x], __pc1))

def PC_2(key: List[int]):
    return list(map(lambda x: key[x], __pc2))

def get_sub_key(key: List[int]):
    key = PC_1(key) # PC-1置换
    L, R = key[:28], key[28:] # 分成两半

    skeys = []

    for i in range(16):
        for j in range(ROTATIONS[i]): # 根据轮次左移
            L = L[1:] + L[:1]
            R = R[1:] + R[:1]

        skeys.append(PC_2(L+R)) # PC-2置换
    
    return skeys

密码函数F

该函数的作用就是将（明文数据的右半部分）32位的数据和48位的数据进行加密得到32位的数据。

拓展置换E：将明文数据的右半部分进行32位扩展为48位。可以叫做位选择函数，也称为E盒。(会发现有些重复取值导致增加了16位)

__expansion_table = [
  31,  0,  1,  2,  3,  4,
   3,  4,  5,  6,  7,  8,
   7,  8,  9, 10, 11, 12,
  11, 12, 13, 14, 15, 16,
  15, 16, 17, 18, 19, 20,
  19, 20, 21, 22, 23, 24,
  23, 24, 25, 26, 27, 28,
  27, 28, 29, 30, 31,  0
]
def EP(data: List[int]):  # 扩展置换
  return list(map(lambda x: data[x], __expansion_table))

异或：将扩展的48位的输出结果我们把它叫做E(Ri),再与48位的子密钥进行异或运算。

  R = list(map(lambda x, y: x ^ y, R, skeys[index]))  # 异或

S盒替换：将异或得到的48位结果分为8个6位的块，然后每一块通过对应的一个S盒产出一个4位的输出，最终就是32位。

__sbox = [...]  # 内容过长，请完整代码文件
B = [R[:6], R[6:12], R[12:18], R[18:24], R[24:30], R[30:36], R[36:42], R[42:]]  # 分成八份
Bn = [0] * 32
pos = 0
for i in range(8):
    #  计算该使用S盒的行坐标和列坐标
    row = (B[j][0] << 1) + B[j][5]
    col = (B[j][1] << 3) + (B[j][2] << 2) + (B[j][3] << 1) + B[j][4]

    sb = __sbox[j][row][col]

    Bn[pos + 0] = (sb & 8) >> 3  # 四位输出
    Bn[pos + 1] = (sb & 4) >> 2
    Bn[pos + 2] = (sb & 2) >> 1
    Bn[pos + 3] = (sb & 1)

    pos += 4

P盒替换：将S盒中得到的32位结果进行P盒置换。

__p = [
15, 6, 19, 20, 28, 11,
27, 16, 0, 14, 22, 25,
4, 17, 30, 9, 1, 7,
23,13, 31, 26, 2, 8,
18, 12, 29, 5, 21, 10,
3, 24
]
def P(data: List[int]):  # P置换
  return list(map(lambda x: data[x], __p))

逆置换

也叫最终置换，就是第一步的置换的逆操作，我们记作
$IP^{-1}$
例如，第一次置换的时候我们把将第1位换到了第40位，那么通过逆置换，就会把第40位换到第1位。置换表格如下。
```
_FP = [
	39,  7, 47, 15, 55, 23, 63, 31,
	38,  6, 46, 14, 54, 22, 62, 30,
	37,  5, 45, 13, 53, 21, 61, 29,
	36,  4, 44, 12, 52, 20, 60, 28,
	35,  3, 43, 11, 51, 19, 59, 27,
	34,  2, 42, 10, 50, 18, 58, 26,
	33,  1, 41,  9, 49, 17, 57, 25,
	32,  0, 40,  8, 48, 16, 56, 24
]

def FP(plain: List[int]):
    return list(map(lambda x: plain[x], _FP))
```

导入密码学库加密脚本如下：

from Crypto.Cipher import DES

import pyDes
des = DES.new(b'12345678',DES.MODE_ECB)

print(des.encrypt(b"12345678"))
des = pyDes.des(b'12345678')
print(des.encrypt(b'12345678'))

加密脚本如下：

from operator import add
from typing import List
from functools import reduce

_IP = [57, 49, 41, 33, 25, 17, 9,  1,
	59, 51, 43, 35, 27, 19, 11, 3,
	61, 53, 45, 37, 29, 21, 13, 5,
	63, 55, 47, 39, 31, 23, 15, 7,
	56, 48, 40, 32, 24, 16, 8,  0,
	58, 50, 42, 34, 26, 18, 10, 2,
	60, 52, 44, 36, 28, 20, 12, 4,
	62, 54, 46, 38, 30, 22, 14, 6
]

def IP(plain: List[int]):
    return list(map(lambda x: plain[x], _IP))

__pc1 = [56, 48, 40, 32, 24, 16,  8,
	  0, 57, 49, 41, 33, 25, 17,
	  9,  1, 58, 50, 42, 34, 26,
	 18, 10,  2, 59, 51, 43, 35,
	 62, 54, 46, 38, 30, 22, 14,
	  6, 61, 53, 45, 37, 29, 21,
	 13,  5, 60, 52, 44, 36, 28,
	 20, 12,  4, 27, 19, 11,  3
]

__pc2 = [
	13, 16, 10, 23,  0,  4,
	 2, 27, 14,  5, 20,  9,
	22, 18, 11,  3, 25,  7,
	15,  6, 26, 19, 12,  1,
	40, 51, 30, 36, 46, 54,
	29, 39, 50, 44, 32, 47,
	43, 48, 38, 55, 33, 52,
	45, 41, 49, 35, 28, 31
]
ROTATIONS = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]

def PC_1(key: List[int]):
    return list(map(lambda x: key[x], __pc1))

def PC_2(key: List[int]):
    return list(map(lambda x: key[x], __pc2))

def get_sub_key(key: List[int]):
    key = PC_1(key) # PC-1置换
    L, R = key[:28], key[28:] # 分成两半

    skeys = []

    for i in range(16):
        for j in range(ROTATIONS[i]): # 根据轮次左移
            L = L[1:] + L[:1]
            R = R[1:] + R[:1]

        skeys.append(PC_2(L+R)) # PC-2置换
    
    return skeys

__expansion_table = [
	31,  0,  1,  2,  3,  4,
	 3,  4,  5,  6,  7,  8,
	 7,  8,  9, 10, 11, 12,
	11, 12, 13, 14, 15, 16,
	15, 16, 17, 18, 19, 20,
	19, 20, 21, 22, 23, 24,
	23, 24, 25, 26, 27, 28,
	27, 28, 29, 30, 31,  0
]
__sbox = [
		# S1
		[14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7,
		 0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8,
		 4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0,
		 15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13],

		# S2
		[15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10,
		 3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5,
		 0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15,
		 13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9],

		# S3
		[10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8,
		 13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1,
		 13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7,
		 1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12],

		# S4
		[7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15,
		 13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9,
		 10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4,
		 3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14],

		# S5
		[2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9,
		 14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6,
		 4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14,
		 11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3],

		# S6
		[12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11,
		 10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8,
		 9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6,
		 4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13],

		# S7
		[4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1,
		 13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6,
		 1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2,
		 6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12],

		# S8
		[13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7,
		 1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2,
		 7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8,
		 2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11],
	]
__p = [
	15, 6, 19, 20, 28, 11,
	27, 16, 0, 14, 22, 25,
	4, 17, 30, 9, 1, 7,
	23,13, 31, 26, 2, 8,
	18, 12, 29, 5, 21, 10,
	3, 24
]

def EP(data: List[int]):  # 扩展置换
    return list(map(lambda x: data[x], __expansion_table))

def P(data: List[int]):  # P置换
    return list(map(lambda x: data[x], __p))

def F(index: int, R: List[int], skeys: List[List[int]]):
    """
    index: 代表这是第几轮
    R: 输入数据
    skeys: 子密钥数组
    """
    R = EP(R)  # 扩展置换
    R = list(map(lambda x, y: x ^ y, R, skeys[index]))  # 异或

    B = [R[:6], R[6:12], R[12:18], R[18:24], R[24:30], R[30:36], R[36:42], R[42:]]  # 分成八份

    Bn = [0] * 32
    pos = 0
    for i in range(8):
        #  计算该使用S盒的行坐标和列坐标
        row = (B[i][0] << 1) + B[i][5]
        col = (B[i][1] << 3) + (B[i][2] << 2) + (B[i][3] << 1) + B[i][4]

        sb = __sbox[i][(row << 4) + col]

        Bn[pos + 0] = (sb & 8) >> 3  # 四位输出
        Bn[pos + 1] = (sb & 4) >> 2
        Bn[pos + 2] = (sb & 2) >> 1
        Bn[pos + 3] = (sb & 1)

        pos += 4
    R = P(Bn)
    return R

_FP = [
	39,  7, 47, 15, 55, 23, 63, 31,
	38,  6, 46, 14, 54, 22, 62, 30,
	37,  5, 45, 13, 53, 21, 61, 29,
	36,  4, 44, 12, 52, 20, 60, 28,
	35,  3, 43, 11, 51, 19, 59, 27,
	34,  2, 42, 10, 50, 18, 58, 26,
	33,  1, 41,  9, 49, 17, 57, 25,
	32,  0, 40,  8, 48, 16, 56, 24
]

def FP(plain: List[int]):
    return list(map(lambda x: plain[x], _FP))


key = b'12345678'
plain = b'12345678'

# 转为二进制数组
key = reduce(add, [list(map(int, bin(i)[2:].zfill(8))) for i in key])
plain = reduce(add, [list(map(int, bin(i)[2:].zfill(8))) for i in plain])
skeys = get_sub_key(key)

block = IP(plain)

L, R = block[:32], block[32:]
for i in range(16):
    tpR = R[:]
    R = F(i, R, skeys)
    R = list(map(lambda x, y: x ^ y, R, L))
    L = tpR
block = R + L
block = FP(block)
enc = bytes([int(''.join(map(str,block[i*8:(i+1)*8])),2) for i in range(8)])
    
print(enc)

解密脚本如下：

from Crypto.Util.number import *
from operator import add
from typing import List
from functools import reduce
# 已知密文c
c = b'\x96\xd0\x02\x88x\xd5\x8c\x89'
# 已知密钥为key    最终结果m为b'12345678'
key = b'12345678'

__pc1 = [56, 48, 40, 32, 24, 16, 8,
         0, 57, 49, 41, 33, 25, 17,
         9, 1, 58, 50, 42, 34, 26,
         18, 10, 2, 59, 51, 43, 35,
         62, 54, 46, 38, 30, 22, 14,
         6, 61, 53, 45, 37, 29, 21,
         13, 5, 60, 52, 44, 36, 28,
         20, 12, 4, 27, 19, 11, 3
         ]

__pc2 = [
    13, 16, 10, 23, 0, 4,
    2, 27, 14, 5, 20, 9,
    22, 18, 11, 3, 25, 7,
    15, 6, 26, 19, 12, 1,
    40, 51, 30, 36, 46, 54,
    29, 39, 50, 44, 32, 47,
    43, 48, 38, 55, 33, 52,
    45, 41, 49, 35, 28, 31
]
ROTATIONS = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]


def PC_1(key: List[int]):
    return list(map(lambda x: key[x], __pc1))


def PC_2(key: List[int]):
    return list(map(lambda x: key[x], __pc2))


def get_sub_key(key: List[int]):
    key = PC_1(key)  # PC-1置换
    L, R = key[:28], key[28:]  # 分成两半

    skeys = []

    for i in range(16):
        for j in range(ROTATIONS[i]):  # 根据轮次左移
            L = L[1:] + L[:1]
            R = R[1:] + R[:1]

        skeys.append(PC_2(L + R))  # PC-2置换

    return skeys
_IP = [57, 49, 41, 33, 25, 17, 9, 1,
       59, 51, 43, 35, 27, 19, 11, 3,
       61, 53, 45, 37, 29, 21, 13, 5,
       63, 55, 47, 39, 31, 23, 15, 7,
       56, 48, 40, 32, 24, 16, 8, 0,
       58, 50, 42, 34, 26, 18, 10, 2,
       60, 52, 44, 36, 28, 20, 12, 4,
       62, 54, 46, 38, 30, 22, 14, 6
       ]

__sbox = [
    # S1
    [14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7,
     0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8,
     4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0,
     15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13],

    # S2
    [15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10,
     3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5,
     0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15,
     13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9],

    # S3
    [10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8,
     13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1,
     13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7,
     1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12],

    # S4
    [7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15,
     13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9,
     10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4,
     3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14],

    # S5
    [2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9,
     14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6,
     4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14,
     11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3],

    # S6
    [12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11,
     10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8,
     9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6,
     4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13],

    # S7
    [4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1,
     13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6,
     1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2,
     6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12],

    # S8
    [13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7,
     1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2,
     7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8,
     2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11],
]
__p = [
    15, 6, 19, 20, 28, 11,
    27, 16, 0, 14, 22, 25,
    4, 17, 30, 9, 1, 7,
    23, 13, 31, 26, 2, 8,
    18, 12, 29, 5, 21, 10,
    3, 24
]
__expansion_table = [
    31, 0, 1, 2, 3, 4,
    3, 4, 5, 6, 7, 8,
    7, 8, 9, 10, 11, 12,
    11, 12, 13, 14, 15, 16,
    15, 16, 17, 18, 19, 20,
    19, 20, 21, 22, 23, 24,
    23, 24, 25, 26, 27, 28,
    27, 28, 29, 30, 31, 0
]
_FP = [
	39,  7, 47, 15, 55, 23, 63, 31,
	38,  6, 46, 14, 54, 22, 62, 30,
	37,  5, 45, 13, 53, 21, 61, 29,
	36,  4, 44, 12, 52, 20, 60, 28,
	35,  3, 43, 11, 51, 19, 59, 27,
	34,  2, 42, 10, 50, 18, 58, 26,
	33,  1, 41,  9, 49, 17, 57, 25,
	32,  0, 40,  8, 48, 16, 56, 24
]

def FP(plain: List[int]):
    return list(map(lambda x: plain[x], _FP))
def EP(data: List[int]):  # 扩展置换
    return list(map(lambda x: data[x], __expansion_table))
def IP(plain: List[int]):
    return list(map(lambda x: plain[x], _IP))
def P(data: List[int]):  # P置换
    return list(map(lambda x: data[x], __p))
def F(index: int, R: List[int], skeys: List[List[int]]):
    """
    index: 代表这是第几轮
    R: 输入数据
    skeys: 子密钥数组
    """
    R = EP(R)  # 扩展置换
    R = list(map(lambda x, y: x ^ y, R, skeys[index]))  # 异或

    B = [R[:6], R[6:12], R[12:18], R[18:24], R[24:30], R[30:36], R[36:42], R[42:]]  # 分成八份

    Bn = [0] * 32
    pos = 0
    for i in range(8):
        #  计算该使用S盒的行坐标和列坐标
        row = (B[i][0] << 1) + B[i][5]
        col = (B[i][1] << 3) + (B[i][2] << 2) + (B[i][3] << 1) + B[i][4]

        sb = __sbox[i][(row << 4) + col]

        Bn[pos + 0] = (sb & 8) >> 3  # 四位输出
        Bn[pos + 1] = (sb & 4) >> 2
        Bn[pos + 2] = (sb & 2) >> 1
        Bn[pos + 3] = (sb & 1)

        pos += 4
    R = P(Bn)
    return R

# 已知key，那么我们可以通过求出16轮每一轮的子密钥。不过key为字节，需要转为2进制。
key = reduce(add, [list(map(int, bin(i)[2:].zfill(8))) for i in key])
skeys = get_sub_key(key)

#  将密文转化为二进制
c = reduce(add, [list(map(int, bin(i)[2:].zfill(8))) for i in c])
# 由于密文是通过逆置换来的，所以我们需要顺置换一次。也就是加密的IP函数。
c = IP(c)
# 将c分成左半部分和右半部分 因为求出的结果前部分为右半，所以记为R，同理后半记为L。
R = c[:32]
L = c[32:]
#  先分析第16轮到第15轮，也就是分析L16、R16  如何到L15、R15，首先L16就是R15 ，然后R16是R15与k16记性F函数加密然后与L15异或得到的。这样的话
#  我们知道R16  R15 就 可以得到L15 。

for i in range(16):

    tmpR = R  # L16赋值给R15 ，因为他两相等
    R = L
    tmp = F(15-i, R, skeys)
    L = list(map(lambda x, y: x ^ y, tmpR, tmp))

# 得到第一轮的L 和R ，需要 再置换一下，明文初始置换的逆置换就是加密的最终置换。
block = L + R
block = FP(block)
m = (long_to_bytes(int((''.join(map(str, block))), 2))) #将得到的结果转化为字符。
print(m)

Aes加密

和Des一样，为了取代Des而出现的新的对称密码标准。最终在2000年选用了名为Rijndael对称密码，将其确认为AES。
基本信息如下
- 1、输入：128bit
- 2、输出：128bit
- 3、SPN（Substitution-permutation network）网络结构（代换-置换网络）
Aes和Des的区别
- Des输入的是64位，Aes是128位
- Des将明文分成两部分，左边和右边，每次都使用密钥对右边的数据进行F函数加密然后和左边数据进行异或得到下一轮右边的数据，然后直接将上一轮右边的数据放在左边。Aes则不会分为左右两边，而是直接对明文进行处理。
- Des的Feilstel中的F函数可以选择可逆，也可以不可逆，因为解密的时候不影响。Aes的SPN需要可逆运算。
AES加密算法图解

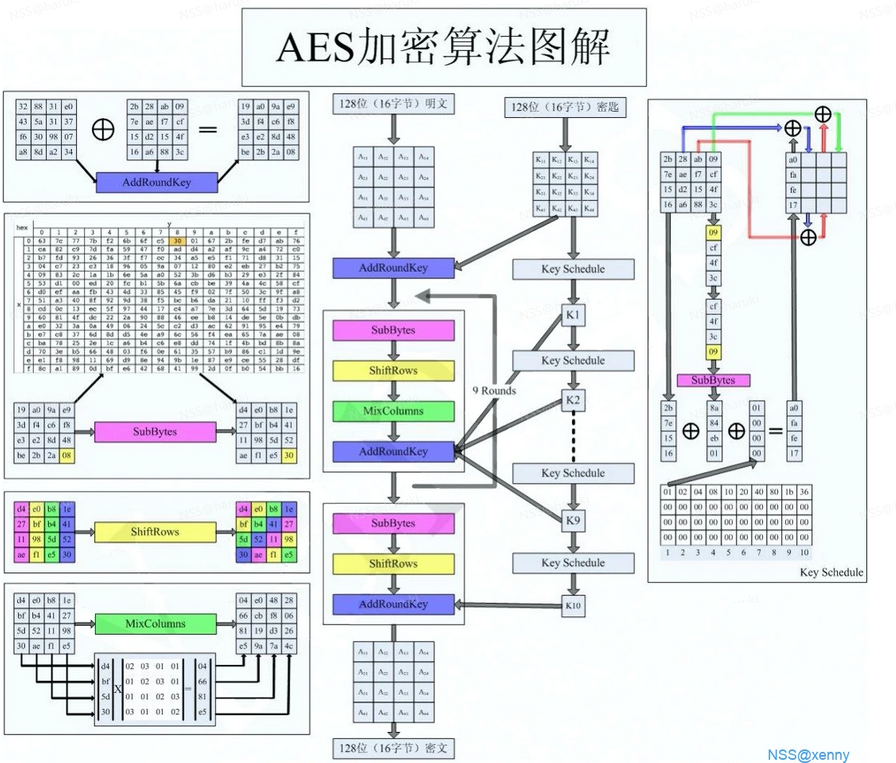
如上图所示，分为左中右三部分，右边是密钥的生成图解，中间是对明文加密的图解，左边是对明文加密中每一个加密的算法图解。
明文加密涉及的操作有4种，密钥如果是128位，进行10轮迭代，如果是192位，进行12轮迭代，如果是256位，进行256轮迭代。这四个操作分别是

1、轮密钥加（AddRoundKey）

2、字节替换（SubBytes）

3、行置换（ShiftRows）

4、列混淆（MixColumn）

那么我们一次来看看是如何操作的

轮密钥加（AddRoundKey）

将明文的每一字节（8bit为一个字节，一共128位，也就是16个字节）放入矩阵中，设得到的矩阵为P，设得到的子密钥矩阵为K（子密钥最后再看看怎么生成）。
$\left[ \begin{matrix} p_{1} & p_{2} & p_{3} & p_{4} \\ p_{5} & p_{6} & p_{7} & p_{8} \\ p_{9} & p_{10} & p_{11} & p_{12} \\ p_{13} & p_{14} & p_{15} & p_{16} \end{matrix} \right]$

$\left[ \begin{matrix} k_{1} & k_{2} & k_{3} & k_{4} \\ k_{5} & k_{6} & k_{7} & k_{8} \\ k_{9} & k_{10} & k_{11} & k_{12} \\ k_{13} & k_{14} & k_{15} & k_{16} \end{matrix} \right]$

那么这个操作就是将P中的每一位与K中的每一位进行异或得到一个新的矩阵。
$\oplus K = \left[ \begin{matrix} p_{1}\oplus k_{1} & p_{2}\oplus k_{2} & p_{3}\oplus k_{3} & p_{4}\oplus k_{4} \\ p_{5}\oplus k_{5} & p_{6}\oplus k_{6} & p_{7}\oplus k_{7} & p_{8}\oplus k_{8} \\ p_{9}\oplus k_{9} & p_{10}\oplus k_{10} & p_{11}\oplus k_{11} & p_{12}\oplus k_{12} \\ p_{31}\oplus k_{13} & p_{14}\oplus k_{14} & p_{15}\oplus k_{15} & p_{16}\oplus k_{16} \end{matrix} \right]$
python代码如下

def sub_bytes(s):
    for i in range(4):
        for j in range(4):
            s[i][j] = s_box[s[i][j]]

字节替换（SubByte）

对于这个操作首先需要引入一个S盒（S box），也就是一个替换表。如下：

0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16,

经过轮密钥加后得到的结果在S盒中找到对应的数据进行替换

python代码如下：

def sub_bytes(s):
    for i in range(4):
        for j in range(4):
            s[i][j] = s_box[s[i][j]]

行置换（ShiftRows）

进行扩散处理。防止攻击者找到明文和密文之间的关系。

核心原理就是第一行不变、第二行左移2位，第三行左移3位，第四行左移4位。如下图：
$\left[ \begin{matrix} p_{1} & p_{2} & p_{3} & p_{4} \\ p_{5} & p_{6} & p_{7} & p_{8} \\ p_{9} & p_{10} & p_{11} & p_{12} \\ p_{13} & p_{14} & p_{15} & p_{16} \end{matrix} \right] \longrightarrow P^{'} = \left[ \begin{matrix} p_{1} & p_{2} & p_{3} & p_{4} \\ p_{6} & p_{8} & p_{8} & p_{5} \\ p_{11} & p_{12} & p_{9} & p_{10} \\ p_{16} & p_{13} & p_{14} & p_{15} \end{matrix} \right]$

python代码如下：

def shift_rows(s):
    s[0][1], s[1][1], s[2][1], s[3][1] = s[1][1], s[2][1], s[3][1], s[0][1]
    s[0][2], s[1][2], s[2][2], s[3][2] = s[2][2], s[3][2], s[0][2], s[1][2]
    s[0][3], s[1][3], s[2][3], s[3][3] = s[3][3], s[0][3], s[1][3], s[2][3]

正常情况下s[0][1] 代表第1行第2个位置的数据，但是我们这里表示第1列第二个位置的数据，例如：
$\left[ \begin{matrix} 1 & 2 & 3 \\ 2 & 2 & 2 \end{matrix} \right] \longrightarrow s_{'}\left[ \begin{matrix} 1 & 2 \\ 3 & 2 \\ 2 & 2 \end{matrix} \right]$
我们把s变成s’，这样我们通过上面python代码就可以实现行置换了，这样的好处就是可以通过s[i]直接获取某一列。

列混淆（MixColumn）

也是扩散操作

将行置换得到的矩阵和P在 GF(2^8) 做乘法，GF代表伽罗瓦域，其实就是计算的结果模上一个2^8即可。

python代码如下：

# 参考 http://cs.ucsb.edu/~koc/cs178/projects/JT/aes.c
xtime = lambda a: (((a << 1) ^ 0x1B) & 0xFF) if (a & 0x80) else (a << 1)

def mix_single_column(a):
    # see Sec 4.1.2 in The Design of Rijndael
    t = a[0] ^ a[1] ^ a[2] ^ a[3]
    u = a[0]
    a[0] ^= t ^ xtime(a[0] ^ a[1])
    a[1] ^= t ^ xtime(a[1] ^ a[2])
    a[2] ^= t ^ xtime(a[2] ^ a[3])
    a[3] ^= t ^ xtime(a[3] ^ u)

def mix_columns(s):
    for i in range(4):
        mix_single_column(s[i])

子密钥生成

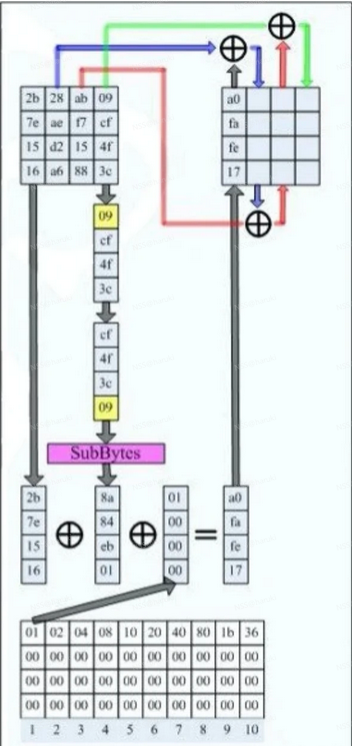
分析一下子密钥如何生成。

1、左上角为密钥，右上角为生成的子密钥，最下面为异或表。
2、异或表有10列，每一列会生成一次子密钥，所以最后会有10个子密钥，每个子密钥都是一个4*4的矩阵
3、从左上角开始看起，先取密钥的第1列，然后将第4进行移位（Shift）然后字节替换（SubBytes），将得到的结果和第一列异或。
4、将第三步得到的结果和异或表中的第一列异或得到子密钥的第一列。
5、将子密钥第1列和密钥第2列异或得到子密钥第2列。
6、将子密钥第2列和密钥第3列异或得到子密钥第3列。
7、将子密钥第3列和密钥第4列异或得到子密钥第4列。

而对于192或是256位密钥会稍微又些不一样，但大致流程相同，这里我们以128位的密钥为例

python脚本如下：

r_con = (0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40,0x80, 0x1B, 0x36)

def xor_bytes(a, b):
    return bytes(i^j for i, j in zip(a, b))

def _expand_key(s):
    for i in range(10):
        word = list(s[-1])  # 取得最后一列
        word.append(word.pop(0)) # 将首位移动到最后
        word = [s_box[b] for b in word]  # SubBytes操作
        word[0] ^= r_con[i]  # 和异或表内数据异或

        s.append(xor_bytes(word, s[-4]))  # 得到新的子密钥
        s.append(xor_bytes(s[-1], s[-4]))  # 因为直接在s中添加，所以本该和上一轮第二列异或的位置还是-4
        s.append(xor_bytes(s[-1], s[-4]))
        s.append(xor_bytes(s[-1], s[-4]))

    return [s[4*i : 4*(i+1)] for i in range(len(s) // 4)]

导入密码学库加密脚本如下：

from Crypto.Cipher import AES
aes = AES.new(b'1234567812345678', AES.MODE_ECB)
print(aes.encrypt(b'1234567812345678'))  # b'm\xac\x1cV\xe7G\xfa\xe0:\xcf\x8ch\x91\xe4(\xe0'

加密脚本如下：

#  轮密钥加（AddRoundKey）
def add_round_key(s, k):
    for i in range(4):
        for j in range(4):
            s[i][j] ^= k[i][j]


s_box = [0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16]

# 字节替换（SubByte）
def sub_bytes(s):
    for i in range(4):
        for j in range(4):
            s[i][j] = s_box[s[i][j]]

# 行置换（ShiftRows）
def shift_rows(s):
    s[0][1], s[1][1], s[2][1], s[3][1] = s[1][1], s[2][1], s[3][1], s[0][1]
    s[0][2], s[1][2], s[2][2], s[3][2] = s[2][2], s[3][2], s[0][2], s[1][2]
    s[0][3], s[1][3], s[2][3], s[3][3] = s[3][3], s[0][3], s[1][3], s[2][3]


# 列混淆（MixColumn）
# 参考 http://cs.ucsb.edu/~koc/cs178/projects/JT/aes.c
xtime = lambda a: (((a << 1) ^ 0x1B) & 0xFF) if (a & 0x80) else (a << 1)

def mix_single_column(a):
    # see Sec 4.1.2 in The Design of Rijndael
    t = a[0] ^ a[1] ^ a[2] ^ a[3]
    u = a[0]
    a[0] ^= t ^ xtime(a[0] ^ a[1])
    a[1] ^= t ^ xtime(a[1] ^ a[2])
    a[2] ^= t ^ xtime(a[2] ^ a[3])
    a[3] ^= t ^ xtime(a[3] ^ u)

def mix_columns(s):
    for i in range(4):
        mix_single_column(s[i])

# 子密钥生成
r_con = (0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40,0x80, 0x1B, 0x36)

def xor_bytes(a, b):
    return bytes(i^j for i, j in zip(a, b))

def _expand_key(s):
    for i in range(10):
        word = list(s[-1])  # 取得最后一列
        word.append(word.pop(0)) # 将首位移动到最后
        word = [s_box[b] for b in word]  # SubBytes操作
        word[0] ^= r_con[i]  # 和异或表内数据异或

        s.append(xor_bytes(word, s[-4]))  # 得到新的子密钥
        s.append(xor_bytes(s[-1], s[-4]))  # 因为直接在s中添加，所以本该和上一轮第二列异或的位置还是-4
        s.append(xor_bytes(s[-1], s[-4]))
        s.append(xor_bytes(s[-1], s[-4]))

    return [s[4*i : 4*(i+1)] for i in range(len(s) // 4)]

# 字节转矩阵
def bytes2matrix(text):
    """ Converts a 16-byte array into a 4x4 matrix.  """
    return [list(text[i:i+4]) for i in range(0, len(text), 4)]

# Aes加密

key = b'1234567812345678'
plain = b'1234567812345678'


skeys = _expand_key(bytes2matrix(key))
plain = bytes2matrix(plain)
add_round_key(plain, skeys[0])

for i in range(1,10):
    sub_bytes(plain)
    shift_rows(plain)
    mix_columns(plain)
    add_round_key(plain,skeys[i])

sub_bytes(plain)
shift_rows(plain)
add_round_key(plain,skeys[-1])
enc = bytes(plain[0]+plain[1]+plain[2]+plain[3])
print(enc)

解密脚本如下：

## AES和DES解密不一样，需要找到逆函数，所以这里的有些逆函数我直接抄wp上的。

#  轮密钥加（AddRoundKey）
def add_round_key(s, k):
    for i in range(4):
        for j in range(4):
            s[i][j] ^= k[i][j]

s_box = [0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16]

# 行置换的逆操作
def inv_shift_rows(s):
    s[0][1], s[1][1], s[2][1], s[3][1] = s[3][1], s[0][1], s[1][1], s[2][1]
    s[0][2], s[1][2], s[2][2], s[3][2] = s[2][2], s[3][2], s[0][2], s[1][2]
    s[0][3], s[1][3], s[2][3], s[3][3] = s[1][3], s[2][3], s[3][3], s[0][3]

inv_s_box = [0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16]
def inv_sub_bytes(s):
    for i in range(4):
        for j in range(4):
            s[i][j] = inv_s_box.index(s[i][j])

# 子密钥生成
r_con = (0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40,0x80, 0x1B, 0x36)

def xor_bytes(a, b):
    return bytes(i^j for i, j in zip(a, b))



def _expand_key(s):
    for i in range(10):
        word = list(s[-1])  # 取得最后一列
        word.append(word.pop(0)) # 将首位移动到最后
        word = [s_box[b] for b in word]  # SubBytes操作
        word[0] ^= r_con[i]  # 和异或表内数据异或

        s.append(xor_bytes(word, s[-4]))  # 得到新的子密钥
        s.append(xor_bytes(s[-1], s[-4]))  # 因为直接在s中添加，所以本该和上一轮第二列异或的位置还是-4
        s.append(xor_bytes(s[-1], s[-4]))
        s.append(xor_bytes(s[-1], s[-4]))

    return [s[4*i : 4*(i+1)] for i in range(len(s) // 4)]

xtime = lambda a: (((a << 1) ^ 0x1B) & 0xFF) if (a & 0x80) else (a << 1)


def mix_single_column(a):
    # see Sec 4.1.2 in The Design of Rijndael
    t = a[0] ^ a[1] ^ a[2] ^ a[3]
    u = a[0]
    a[0] ^= t ^ xtime(a[0] ^ a[1])
    a[1] ^= t ^ xtime(a[1] ^ a[2])
    a[2] ^= t ^ xtime(a[2] ^ a[3])
    a[3] ^= t ^ xtime(a[3] ^ u)

def mix_columns(s):
    for i in range(4):
        mix_single_column(s[i])
def inv_mix_columns(s):
    # see Sec 4.1.3 in The Design of Rijndael
    for i in range(4):
        u = xtime(xtime(s[i][0] ^ s[i][2]))
        v = xtime(xtime(s[i][1] ^ s[i][3]))
        s[i][0] ^= u
        s[i][1] ^= v
        s[i][2] ^= u
        s[i][3] ^= v

    mix_columns(s)

def bytes2matrix(text):
    """ Converts a 16-byte array into a 4x4 matrix.  """
    return [list(text[i:i+4]) for i in range(0, len(text), 4)]
# 由于AES解密就是对加密的逆过程。那么第一步先将密文转化为矩阵
c  = b'm\xac\x1cV\xe7G\xfa\xe0:\xcf\x8ch\x91\xe4(\xe0'
key = b'1234567812345678'
c = bytes2matrix(c)
# 然后 轮密钥加的逆操作。轮密钥加的操作是将P和K的每一项进行异或，可以我们找到K，在进行一次轮密钥加即可得到源数据。所以我们这里直接引入轮密钥加方法。放在前面函数区。
# 生成子密钥
skeys = _expand_key(bytes2matrix(key))
# 进行最后一轮的轮密钥加逆操作
add_round_key(c,skeys[-1])

# 接着是行置换的逆操作，行置换目的是起到扩散作用的，将矩阵的位置做了一个移动，那么我们找到一个函数可以移动回去的即可。
inv_shift_rows(c)
# 接着是字节替换的逆操作，那么就是找到其逆表进行替换即可。
inv_sub_bytes(c)
for i in range(9,0,-1):
    add_round_key(c,skeys[i])
    # 列混淆的逆操作
    inv_mix_columns(c)
    # print(c)
    inv_shift_rows(c)
    inv_sub_bytes(c)
add_round_key(c, skeys[0])
m = bytes(c[0]+c[1]+c[2]+c[3])
print(m)

参考

https://www.nssctf.cn/（探索工坊）