ECC椭圆曲线学习

ECC椭圆曲线学习

Elliptic Curve Cryptography

一、数学问题：离散对数难以求解？

$$给定大素数p、g、y=g^{x}modp。$$
$$如果已知x，要求y，很容易计算得到，但是如果知道y，要求x，那么就很困难了。$$
$$这里的对数不是常规的对数而是离散对数。所以逆向求解非常困难。$$

• p在ECC代表模数（用来取模的数）。
• g是代表生成元（高中学习的基数，在ECC中称之为基点）。
• 生成元是数论和抽象代数中的术语。在一个群中（他是一种特殊的代数结构，包含一个操作用来组合群的元素）中，如果存在一个元素g，其各个整数次幂可以生成群中的所有元素（包括群的单位元和其逆元），那么这个元素g就被称为该群的生成元。

例如： 假设我们有一个模 p 的乘法群， p 是一个质数，群的元素是 { 1 , 2 , 3 , . . . , p − 1 } 。在这个群中有一个元素 g ， 能够使得 { g 1 , g 2 , g 3 , . . . , g p − 1 } 模 p 下能生成群中所有的元素， 我们成 g 为一个生成元。 实例： p = 5 那么乘法群为： { 1 , 2 , 3 , 4 , 5 } 例如：\\ 假设我们有一个模p的乘法群，\\p是一个质数，群的元素是\{1,2,3,...,p-1\}。在这个群中有一个元素g，\\能够使得\{g^1,g^2,g^3,...,g^{p-1}\} 模p下能生成 群中所有的元素，\\我们成g为一个生成元。\\\\\\ 实例：\\ p = 5 那么乘法群为：\{1,2,3,4,5\}\\ 例如：假设我们有一个模p的乘法群，p是一个质数，群的元素是{1,2,3,...,p−1}。在这个群中有一个元素g，能够使得{g1,g2,g3,...,gp−1}模p下能生成群中所有的元素，我们成g为一个生成元。实例：p=5那么乘法群为：{1,2,3,4,5}
生成元 g 为 2 ， { 2 1 , 2 2 , 2 3 , 2 4 , 2 5 } 模 5 的结果为 { 2 , 4 , 3 , 1 , 5 } 可以看到里面所有的元素都在乘法群中，所以 g 为这个乘法群的生成元 生成元g 为 2， \{2^1,2^2,2^3,2^4,2^5\} 模 5的 结果为\{2,4,3,1,5\} \\ 可以看到里面所有的元素都在乘法群中，所以g为这个乘法群的生成元 生成元g为2，{21,22,23,24,25}模5的结果为{2,4,3,1,5}可以看到里面所有的元素都在乘法群中，所以g为这个乘法群的生成元

二、什么是椭圆曲线？

2.1、椭圆曲线的标准方程

$$y^2=x^3+ax+b$$

2.2、椭圆曲线的坐标图

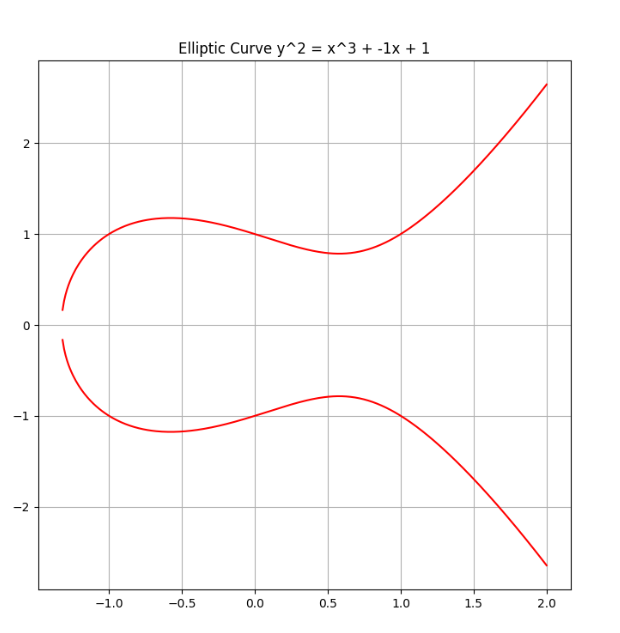
import numpy as np
import matplotlib.pyplot as plt

# 设定参数
a = -1
b = 1

# 定义x范围
x = np.linspace(-2, 2, 400)

# 计算正负 y 值
y_positive = np.sqrt(x**3 + a * x + b)
y_negative = -np.sqrt(x**3 + a * x + b)

# 画图
plt.figure(figsize=(8,8))
plt.plot(x, y_positive, 'r')  # 画出正值部分
plt.plot(x, y_negative, 'r')  # 画出负值部分
plt.title('Elliptic Curve y^2 = x^3 + {}x + {}'.format(a,b))
plt.grid()
plt.show()

三、椭圆曲线密码（ECC）加解密过程

3.1、生成密钥

首先选择一个椭圆曲线、并定义其域（一般是大素数）。然后选择曲线上的一点作为基点G，私钥是选择的神秘数字d，公钥是基点乘以私钥后的点P。（既P = d*G）

例如：

（1） 选择一个椭圆曲线
$$\begin{gathered} 椭圆曲线为y^2=x^3+0\ast x+7(mod233) \\ 其中a=0,b=7,GF(233)。 \\ 所以椭圆曲线为y^2=x^3+7(mod233) \end{gathered}$$
（2）选择一个基点

F = GF(233)           # 定义有限域
E = EllipticCurve(F, [0, 0, 0, 0, 7]) #生成椭圆曲线
E.gens()           #计算椭圆曲线的基点

$$生成基点基点G(9,81)$$

（3）选择一个私钥d
$$选择d=5为私钥。$$
（4）计算公钥

F = GF(233)   # 定义有限域 
E = EllipticCurve(F, [0, 0, 0, 0, 7])   #生成椭圆曲线
G = E.gens()[0]   #计算椭圆曲线的基点G
d = 5             #设置私钥d为5
P = d*G             #计算公钥P
print(P)

$$得到公钥P点为P(191,180)$$

3.2、加密

$$\begin{gathered} 对消息进行椭圆曲线加密，先将消息转为为长整型数据M， \\ 然后将数据M转为椭圆曲线上的一个点C，假设C点的坐标为(X_c,Y_c)， \\ 那么C点坐标怎么算呢，我们需要取一个随机数k \\ {X}_c=kG \\ {Y}_c=M+kP \\ 所以C点为C(kG,M+kP),其中G为基点，P为dG。 \\ 这个C(kG,M+kP)点就是密文。 \end{gathered}$$

3.3、解密

$$\begin{gathered} 我们需要对C(kG,M+kP)进行解密。 \\ kP=kdG \\ M+kP=M+d\ast kG \\ 由于kG为C点横坐标（kG）已知， \\ 所以我们只需要对C点的横坐标（kG）乘以私钥d，就是kP \\ 然后再用C点的纵坐标减去kP就是M。 \\ 然后将长整型数据转为消息，就是我们的明文。 \end{gathered}$$

3.4、通过P和Q难求私钥d

$$\begin{gathered} 我们之前讲了离散对数难以求解，对于椭圆曲线离散对数（ECDLP） \\ 问题也是一样困难的。离散对数（DLP）讲了y=g^{x}modp求解x是非常困难的 \\ 椭圆曲线离散对数（ECDLP）在椭圆曲线y^2=x^3+ax+b上的两个点P，G， \\ 想要求P=k\ast G中的k是非常困难的。求没有算法可以直接求， \\ 然后爆破k的话，如果k比较大，爆破的时间也非常长，所以我们认为非常困难。 \end{gathered}$$