继续是机器学习课程的笔记,这节课的内容是介绍支持向量机(SVM)的内容。SVM是一个非常强大且流行的算法,在一些情况下,面对一些复杂的非线性问题可以提供比逻辑回归或神经网络更加简洁更加有效的结果。
优化目标
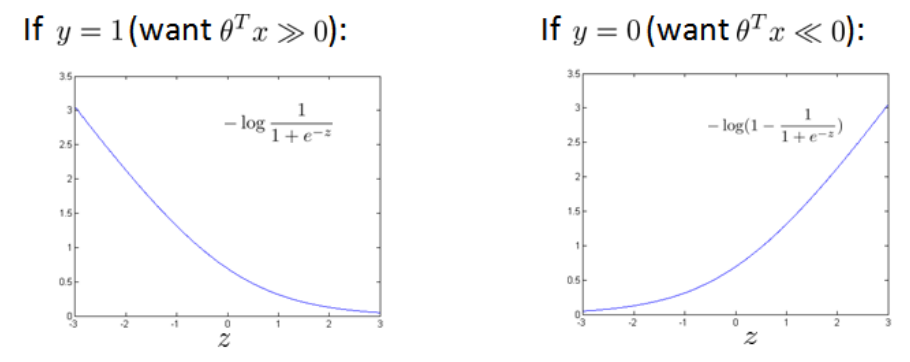
首先是以逻辑回归为例展开讨论,逻辑回归的模型是 hθ(x)=11+e−θTx ,这里分 y=1 和 y=0 两种情况讨论:
- y=1 时,希望假设的 hθ(x)≈1 ,也就是令 z=θTx≫0
- y=0 时,希望假设的 hθ(x)≈0 ,也就是令 z=θTx≪0
从代价函数来看,逻辑回归的代价函数如下所示:
对于任意训练集中的一个实例,对总的代价的影响为
为了让每个实例造成的代价都尽可能地小,这里也说分 y=1 和 y=0 两种情况讨论,如下图所示,最佳的情况是代价为0,但由下图中曲线可以看出,代价始终会存在,且不为0。
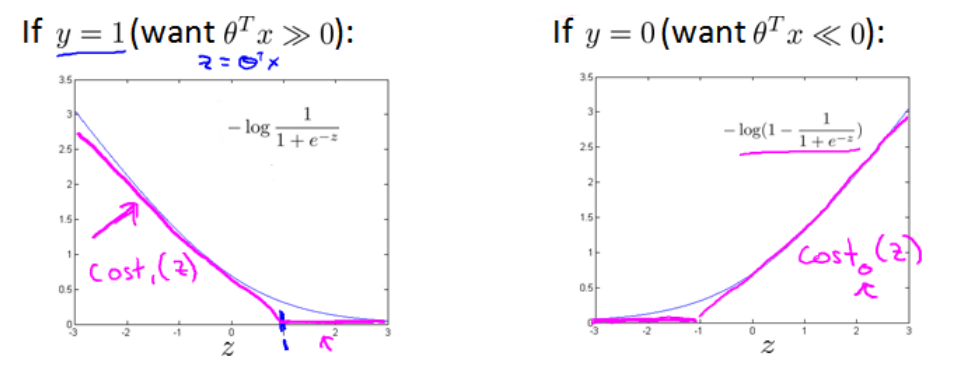
而在SVM中,我们将曲线的代价函数转变成由两条线段构成的折线,如下图所示:
- y=1 时,希望构建的新代价函数如 cost1(z) 所示,当 z≥1 时, cost1(z)=0
- y=0 时,希望构建的新代价函数如 cost0(z) 所示,当 z≤−1 时, cost0(z)=0
用两个新构建的代价函数替换原来逻辑回归的代价函数,得到:
这里对上面的代价函数作如下调整:
- 因为 1m 实际上不影响最优化的结构,将其去掉
- 因为归一化参数 λ 控制的是归一化这一项在整个代价函数中占的比例,对于SVM,我们想要控制的新构建的代价函数部分,因此我们去掉 λ 的同时给第一项乘以一个常数C,相当于我们将整个代价函数除以了 λ ,且 C=1λ
我们依旧是希望能找出使得该代价函数最小的参数。注意,调整后的代价函数是一个凸函数,而非之前逻辑回归那样的非凸函数,这意味着,求解的过程中,不会陷入局部最小值而错过全局最小值的情况,修改后的代价函数如下:
最后给出SVM的假设为:
注意,这里给出的假设在预测时是以z与0的大小关系作为依据的,但是,在训练函数时,我们是以正负1为依据的,这是SVM与逻辑回归的一个关键区别,且导致了后面将介绍的支持向量机的特性。
支持向量机的判定边界
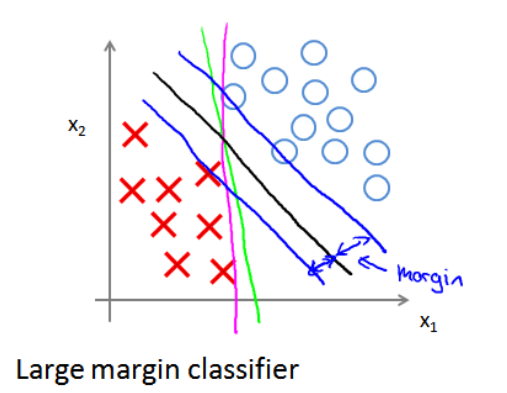
SVM有的时候也被称为最大间隔分类器(Large Margin Classifer),其原因是:SVM可以尝试发现一个与样本数据集之间有着最大间隔的判定边界。
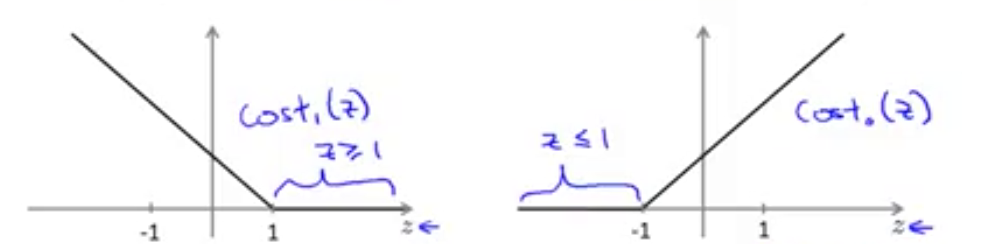
上一小节得到了SVM的代价函数表达式,并且其跟逻辑回归的区别是新构建了两个函数 cost1(z)和cost0(z) ,其图像分别如下所示
由此可以得知,为了最小化代价函数:
- y=1 时,希望 z≥1 时,即 θTx≥1
- y=0 时,希望 z≤−1 时,即 θTx≤−1
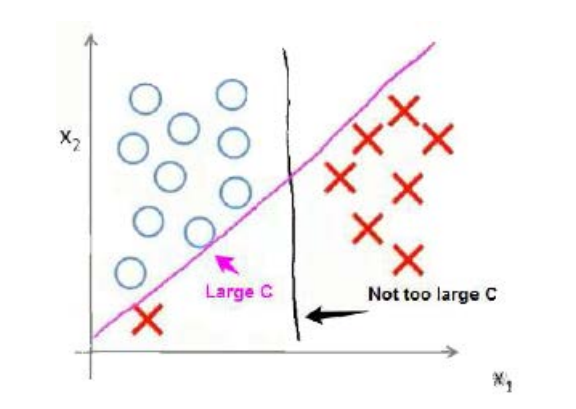
下图是一个可以用直线来区分的分类问题实例,图中绿色和红色的两条线代表作两条逻辑回归的判定边界,而黑色的线代表的则是SVM的判定边界,从图上可以看出黑色的线似乎是更加合理,蓝色的两条线代表的是SVM的判定边界与样本数据之间的间隔,从这幅图也可以看出SVM被称为最大间隔分类器的原因。
接下来是考虑下在SVM中归一化常数C的作用。
假设选择的C是一个非常大的值,那么在最小化代价函数的过程中,我们希望找出在
y=1
和
y=0
两种情况下都使得代价函数中第一项尽量为0的参数,如果我们找到这样的参数,则我们的最小化问题便转变成:
在这种情况下,我们得出的SVM判定边界就是上面黑线那样,具有尝试使得判定边界与样本数据间间隔最大的特性。
但是,使得判断边界与样本数据之间间隔最大并总是好事,假设,我们的数据集如下图所示:
也就是在数据集中间有一个较为明显的异常值,即图中左侧在圆圈处下方的红色叉数据,此时如果选择较大的常数C,会得到图中红色的直线,这样并非很合理,但如果选择较小的C,可能会得到图中黑色直线所示的判定边界。也就是说,C值越小,SVM对异常值越不敏感。
回顾 C=1λ ,有:
- C较大时,相当于 λ 较小,可能会导致过拟合,高偏倚
- C较小时,相当于 λ 较大,可能会导致低拟合,高偏差
核函数
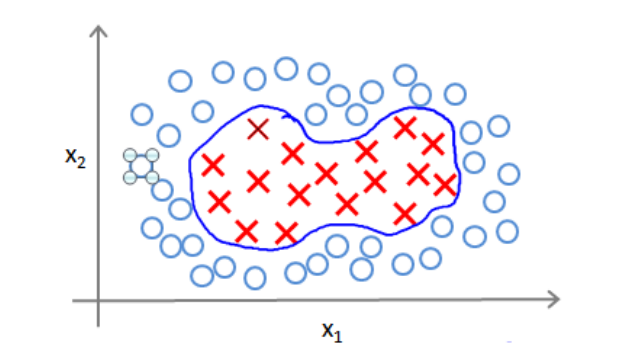
接下来是介绍如何修改SVM算法来解决一些非线性分类的问题。
首先是回顾之前讨论的一个使用高次的多项式模型来解决的一个无法用直线进行分类的问题,其样本集如下图所示:
为了获得上图所示的判定边界,使用的模型可能是 θ0+θ1x1+θ2x2+θ3x1x2+θ4x21+θ5x22+⋯ 的形式。
这里使用一系列新的特征
f
来替换模型中的每一项,如令:
使用核函数计算出新的特征
给定一个训练实例x,可以利用x的各个特征与预先选定的地标(landmarks) l(1),l(2),l(3) 的近似程度来选取新的特征 f1,f2,f3 。如下图所示
这里可以使用如相似度函数来计算新的特征,如令: f1=similarity(x,l(1))=exp(−||x−l(1)||22σ2) ,其中 ||x−l(1)||2=∑nj=1(xj−l(1)j)2 ,表示实例x中所有的特征与地标 l(1) 之间的距离的和。
这里的相似度函数 similarity(x,l(1)) 就是核函数,实质上这就是一个高斯核函数,注意,这个函数与正态分布没有什么实际上的关系,只是看上去像而已。
这些地标的作用是什么呢?如果一个训练实例x与地标L之间的距离近似于0,则新特征f近似于 e−0=1 ;而如果x与L之间距离非常远,则f近似于0。
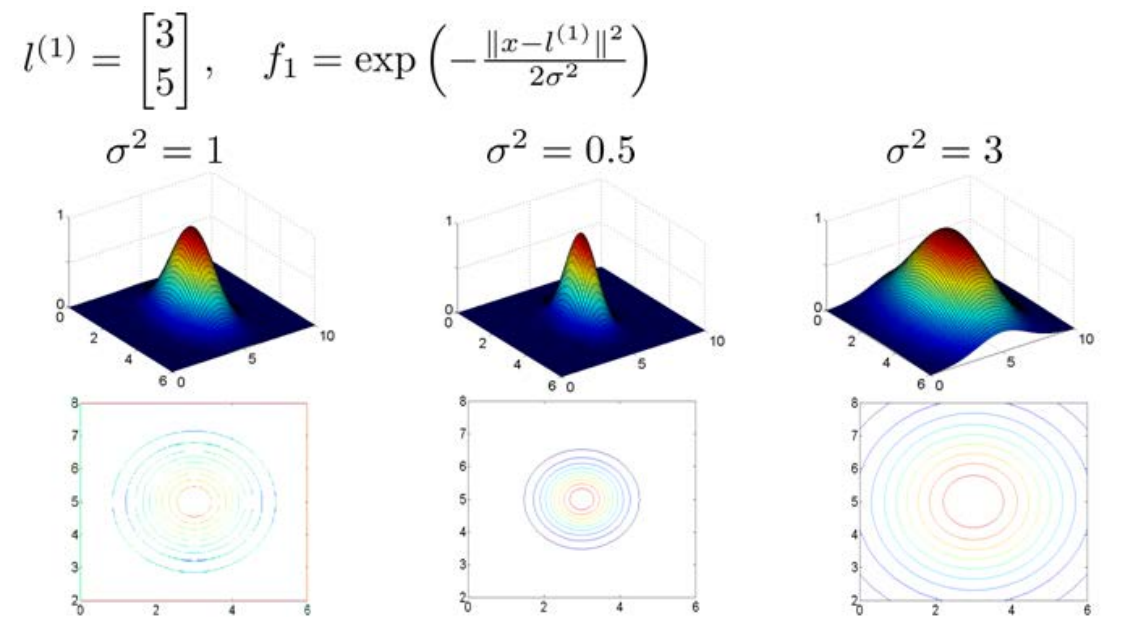
这里假设训练实例含有两个特征 [x1,x2] ,给定地标 l(1) 与不同的 σ ,如下图所示:
上图中水平面的坐标为 x1,x2 ,垂直坐标代表f。可以看出只有当x与 l(1) 重合时,f才具有最大值,随着x的改变,f值改变的速率受到 σ2 的控制。
下图是另外一个例子,图中有3个地标,模型 hθ(x)=θ0+θ1f1+θ2f2+θ1f3 ,令 θ0=−0.5,θ1=θ2=1,θ3=0 ,当实例处于红色的点位置时,因为离 l(1) 更近,但是离 l(2)和l(3) 较远,则有 f1≈1,f2=f3≈0 ,因此 hθ(x)≥1 ,预测 y=1 。同理可以求出对于离 l(2) 较近的绿色点,也预测 y=1 ,但对于青蓝色的点,距离三个点都比较远,所以预测 y=0 ,从而可以得到图中红色的封闭曲线的范围内都是预测 y=1 ,而曲线外部就是预测 y=0 。
因此,在预测的时候,我们采用的特征不是训练实例本身的特征,而是通过核函数计算出的新特征 f1,f2,f3 。
选择地标
一般是根据训练集的数量来选择地标的数量,即如果训练集有m个实例,则选择m个地标,并且令 l(1)=x(1),l(2)=x(2),…,l(m)=x(m) 。这样做的好处是:得到的新特征是建立在原有特征与训练集中所有其他特征之间的距离的基础之上的,即:
下面将核函数应用到SVM到,修改SVM的假设为:
给定x,计算新特征f,当
θTf≥0
时,预测
y=1
,否则反之。
相应地修改代价函数为: minθC∑mi=1[y(i)cost1(θTf(i))+(1−y(i))cost0(θTf(i))]+12∑n=mj=1θ2j
而在具体实施过程中,对最后一项需要做点调整,计算 ∑n=mj=1θ2j=θTθ 时,使用 θTMθ 代替 θTθ ,其中 M 是根据选择的核函数而不同的一个矩阵,这样做的原因是为了简化运算。
理论上讲,我们也可以在逻辑回归中使用核函数,但是上面使用
这里不介绍最小化SVM的代价函数的方法,可以使用现有的软件包(如liblinear,libsvm等)。在使用这些软件包最小化我们的代价函数的时候,通常需要编写核函数,并且如果我们使用高斯核函数,在使用前进行特征缩放是非常必要的。
另外,SVM也可以不用核函数,不使用核函数又称为线性核函数,当不采用非常复杂的函数,或者训练集特征非常多而实例非常少的时候,可以使用这种不带核函数的SVM。
下面是SVM的两个参数 C和σ 的影响:
- C较大时,相当于 λ 较小,可能会导致过拟合,高偏倚
- C较小时,相当于 λ 较大,可能会导致低拟合,高偏差
- σ 较大时,特征f会比较平滑,导致低拟合,高偏差
- σ 较小时,特征f会相对没有那么平滑,导致过拟合,高偏倚
在高斯核函数外,还有其他一些核函数,如:
- 多项式核函数(Polynomial Kernel)
- 字符串核函数(String Kernel)
- 卡方核函数(chi-square kernel)
- 直方图交集核函数(histogram intersection kernel)
- etc…
这些核函数的模板也都是根据训练集和地标之间的距离来构建新的特征,这些核函数需要满足Mercer’s定理,才能被SVM的优化软件正确处理。
多类分类
在之前的逻辑回归这节课中,曾接受一对多的方法来解决一个多类分类问题。即如果一共有k个类,则需要使用k个模型,以及k个参数向量 θ 。
同样地,我们也可以训练k个SVM来解决多类分类问题。但是现在大多数SVM软件包都有内置的多类分类功能,可以直接使用。
逻辑回归和SVM
对于逻辑回归和SVM两种算法,应该如何根据不同问题来选择,下面给出选择的准则:
- 如果相较于m而言,n要大很多,即训练集数据量不够支持训练一个复杂的非线性模型,则选择使用逻辑回归模型或者不带核函数的SVM
- 如果n较小,而且m大小中等,例如n在1-1000之间,而m在10-10000之间,可以使用带高斯核函数的SVM
- 如果n较小,而m较大,例如n在1-1000之间,而m大于50000,则使用SVM会比较慢,解决方案是创造、增加更多的特征,然后使用逻辑回归或者不带核函数的SVM
值得一提的是,神经网络在以上三种情况下都可能会有较好的表现,但是训练神经网络可能会非常慢,选择SVM的原因主要在于它的代价函数是凸函数,不存在局部最小值。
小结
本节课主要介绍一个非常流行的算法–支持向量机(SVM),不过要真正弄懂这个算法的原理,单纯看完这节课其实感觉还是不太够的,还需要更深入了解,并且要顺便用代码实现下,通过实践来促进理解。










 继续是机器学习课程的笔记,这节课的内容是介绍支持向量机(SVM)的内容。SVM是一个非常强大且流行的算法,在一些情况下,面对一些复杂的非线性问题可以提供比逻辑回归或神经网络更加简洁更加有效的结果。:
继续是机器学习课程的笔记,这节课的内容是介绍支持向量机(SVM)的内容。SVM是一个非常强大且流行的算法,在一些情况下,面对一些复杂的非线性问题可以提供比逻辑回归或神经网络更加简洁更加有效的结果。:
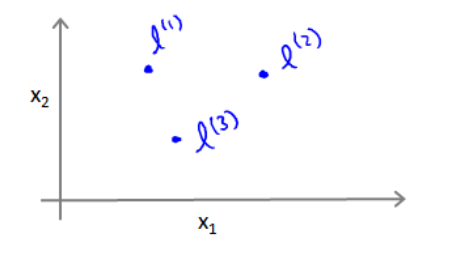
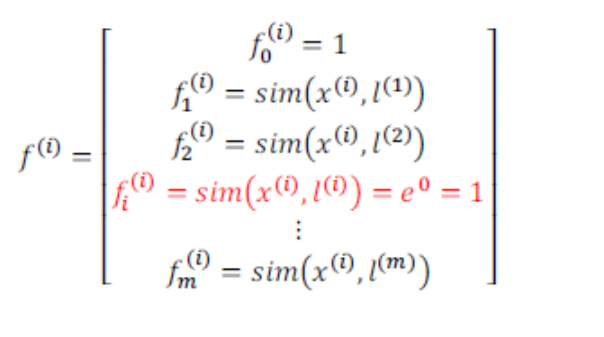















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










