性能指标、参数概念

不断进步的咕咕怪

已于 2024-11-08 16:01:13 修改

阅读量1.8k

点赞数 29

分类专栏：人工智能理论知识文章标签：人工智能机器学习

于 2024-06-25 21:29:14 首次发布

本文链接：https://blog.csdn.net/lcl13193673272/article/details/139958785

版权

人工智能理论知识专栏收录该内容

5 篇文章

订阅专栏

一、BLEU Score是什么（评估机器翻译或文本生成质量的指标）

BLEU Score是一种评估机器翻译或文本生成质量的指标。它是由IBM的研究人员在2002年提出的。

BLEU（Bilingual Evaluation Understudy）的计算基于短语匹配，它将机器生成的句子与参考句子进行比较，计算出它们之间的相似度。具体来说，它会计算机器生成的句子和参考句子之间的n-gram（n元语法）重叠程度，并根据这些重叠的程度来计算一个得分。

BLEU Score的值介于0到1之间，1表示完全匹配，0表示没有匹配。通常情况下，得分越高，说明机器生成的句子与参考句子越接近，也就是翻译的质量越好。

需要注意的是，虽然BLEU Score是一个广泛使用的指标，但它也有一些局限性。例如，它不能很好地处理句子结构的变化，也不能评估翻译的流畅性和自然度。因此，在评估机器翻译或文本生成的质量时，通常会结合其他指标一起使用。

二、困惑度perplexity（概率模型对于给定数据集的不确定度或者说是预测能力的一个指标）

perplexity是用来衡量一个概率模型对于给定数据集的不确定度或者说是预测能力的一个指标。它是模型预测下一个 token（比如单词、字符等）的概率的一个逆指标，因此，perplexity越低，表示模型对数据的理解越好，预测能力越强。

泛指模型在面对复杂数据或异常情况时的表现状态，表示模型对输入数据的理解程度或不确定性。

三、spearman（两个变量之间等级顺序的相关性）

Spearman等级相关系数（Spearman's rank correlation coefficient）是统计学中衡量两个变量间 monotonic（单调）关系强度和方向的一个非参数方法。它通过比较两个变量各自观测值的排序位置（即等级）来计算相关性，而不是直接使用原始数值。Spearman相关系数的取值范围从-1到1，其中：

1 表示完全正相关，即一个变量增加时，另一个变量也严格按确定的比例增加。
0 表示没有单调关系，即两个变量的变化相互独立。
-1 表示完全负相关，即一个变量增加时，另一个变量按确定的比例减少。

在Evo模型的研究中，Spearman相关系数被用来量化模型预测的序列概率（如序列似然性或伪似然性）与实验测量的适应度值（代表分子功能的实验评估结果）之间的关联性。如果Spearman相关系数接近1或-1，说明模型预测与实际功能变化之间有很强的正向或反向单调关系；若接近0，则说明模型预测与实验结果之间缺乏明显的单调关系。

此外，文中还提到了利用t分布来评估Spearman相关系数的统计显著性。这意味着，研究者会基于样本数量N来计算一个P值，判断观测到的相关性是否不太可能仅由随机变异引起。如果P值小于预设的显著性水平（如0.05），则认为模型预测与实验结果之间的相关性是统计显著的。在Python编程中，scipy库常被用来执行这类统计测试。

四、PCC（皮尔逊相关系数，衡量两个变量间线性相关程度）

PCC（Pearson Correlation Coefficient，皮尔逊相关系数）是一种衡量两个变量之间线性相关程度的统计量。它描述了两个变量的标准分数（z分数）之间的线性关系强度和方向。PCC的取值范围是-1到1，其中1表示完全正相关，-1表示完全负相关，0表示没有相关性。

在生物学和生物信息学中，PCC常用于评估预测值与实际值之间的相关性。例如，在RNA溶剂可及性预测任务中，PCC可以用来衡量模型预测的溶剂可及性值与实验测量值之间的相关性。PCC值越高，说明模型的预测值与实际值之间的关联性越强，模型的预测性能越好。

五、ASA是什么？（溶剂可及性面积）

ASA代表溶剂可及性面积（Solvent Accessible Surface Area），它是衡量RNA链中单个核苷酸暴露于溶剂或其他功能性生物分子的程度的指标。ASA的计算通常是通过POPS软件包完成的，使用1.4埃的探针半径。所有ASA值都被归一化为相对可及表面面积（RSA），即将ASA值除以相应核苷酸的最大ASA值（腺嘌呤和鸟嘌呤为400埃²，尿嘧啶和胞嘧啶为350埃²）。

六、决定系数R²

在实际应用中，R²常用于评估回归模型的有效性，判断模型是否能够有效地描述数据间的关系。

R²的值介于0和1之间，代表了解释变量（自变量）对于响应变量（因变量）的变异性的解释比例。

如果R²的值越接近1，这表明模型能够更好地拟合数据，预测结果也更为准确。

决定系数R²(R-squared)的数值在0.7到0.9之间通常被认为是比较好的，这表示模型能够解释大部分因变量的变异性。

七、混淆矩阵

真阳性（TP）：判断为真，实际也为真；
伪阳性（FP）：判断为真，实际为假；
伪阴性（FN）：判断为假，实际为真；
真阴性（TN）：判断为假，实际也为假；

TPR（真阳性率）：在所有实际为真的样本中，被正确预测为真的概率：

FPR（伪阳性率）：在所有实际为假的样本中，被错误预测为真的概率；

八、准确率、精确度、召回率、特异性、

准确率

指分类模型正确预测的样本数占总样本数的比例。

特异性

预测正确的负样本数除以所有的实际负样本数

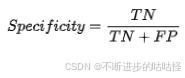
精确度（Precision）

预测为正样本的样本中，实际为正样本的比例。

召回率/敏感性/真正例率（Recall）

实际为正样本的样本中，预测为正样本的比例。

九、PR曲线和AUC_PR（Area Under the Precision-Recall Curve）

PR曲线（Precision-Recall Curve）：PR曲线展示了在不同阈值下精确度与召回率之间的关系。

AUC_PR值指的是精确度-召回率曲线下的面积。用于衡量分类模型的性能，特别是数据集不平衡的情况下，它比准确率更能反映模型的表现。AUC的值同样介于0.5到1之间，值越接近1，越接近右上角，曲线面积就越大，说明模型在特定召回率下的精确度越高。

十、ROC曲线和AUROC（AUC）

ROC曲线以真正例率（True Positive Rate，也称为召回率或灵敏度）为纵轴，假正例率（False Positive Rate）为横轴，展示了模型在不同阈值下的分类表现。ROC曲线越靠近左上角，表示模型性能越好，因为此时真正例率较高而假正例率较低。

AUROC（AUC）是ROC曲线下方的面积，用于量化模型的分类性能。AUC的取值范围在0到1之间，其中0.5表示模型性能等同于随机猜测，1表示完美分类器。因此，AUC越接近1，越靠近左上角，说明模型在不同阈值下的性能越好。

AUC即area under curve的缩写，一般情况下指的是ROC曲线的AUC，即AUROC，但也可能指的是其他curve下的面积。

ROC曲线确实十分常用，但是在面对类别不均衡数据的时候，ROC曲线却可能产生误导性结果。此时，更推荐使用的是PR曲线。

十一、Balanced Accuracy Mean平衡准确率

平衡准确率，是用于评估多类别分类模型性能的一个指标，特别是在处理类别不平衡问题时。它通过计算每个类别的真正例率（True Positive Rate）的平均值来避免准确率对少数类别的忽视。

十二、F1 score（衡量分类模型性能）

一种常用的评估指标，用于衡量分类模型的性能，特别是在不平衡数据集的情况下。它是精确度（Precision）和召回率（Recall）的调和平均值，F1分数的计算公式为：F1 = 2 * (精确率 * 召回率) / (精确率 + 召回率)。

精确率是指模型预测为正类的样本中，实际为正类的比例；召回率是指实际为正类的样本中，模型预测为正类的比例。

F1 score的取值范围是0到1，其中1表示模型的性能最好，即精确度和召回率都达到了最高。

F1 score常用于二分类问题，但也可以扩展到多分类和多标签分类问题。在RNA结构预测任务中，F1 score可以用来评估模型预测的碱基配对或溶剂可及性等二分类问题的性能。

十三、MCC（衡量二分类问题性能的指标）

MCC（Matthews Correlation Coefficient，马修斯相关系数）是一种衡量二元分类问题性能的指标，特别是在不平衡数据集的情况下。它结合了精确度（Precision）和召回率（Recall）的信息，同时考虑了真正例（True Positives, TP）、假正例（False Positives, FP）、真负例（True Negatives, TN）和假负例（False Negatives, FN）四个分类结果。

MCC的取值范围是-1到1，其中1表示完美预测，-1表示完全错误的预测，0表示预测性能与随机猜测相当。MCC的优点在于它不受数据集中类别不平衡的影响，因此在处理不平衡数据集时，MCC通常被认为是一个比准确率（Accuracy）更可靠的性能指标。

在RNA结构预测任务中，MCC可以用来评估模型预测的准确性，特别是在预测碱基配对或溶剂可及性等二分类问题时。

十四、MAE（衡量模型预测值与实际值之间的差异）

MAE是一种常用的回归问题评估指标，用于衡量模型预测值与实际值之间的差异。它是实际值与预测值之差的绝对值的平均数。

MAE的值越小，表示模型的预测值与实际值之间的差异越小，模型的预测性能越好。MAE不考虑误差的方向，只关心误差的大小，因此它对异常值的敏感度较低。在RNA溶剂可及性预测等回归任务中，MAE常被用作模型性能的评价指标。

十五、交叉验证

交叉验证

通过将数据集分为训练集和测试集，可以在训练集上拟合模型并在测试集上评估其性能。通过多次重复这个过程，可以得到模型在不同数据子集上的平均性能，从而减少因数据划分带来的偶然性和不确定性。

比如：五重交叉验证

是指将数据集分成五份，每次使用四份作为训练集，剩下的一份作为测试集，这个过程重复五次，每次选择不同的数据作为测试集。这样做的目的是减少因数据划分不同而导致的方差，从而更准确地评估模型的泛化能力。

十六、网格搜索

一种超参数调优的方法，它通过遍历预先定义的超参数组合来进行搜索，以找到最佳的参数配置

十七、RMSD（root mean square error）和ϵRMSD

方均根偏移(RMSD):

也称均方根差（RMSE)，是观测值与真值偏差的平方和与观测次数n比值的平方根，是用来衡量观测值同真值之间的偏差。RMSE是一种常用的测量数值之间差异的量度，其数值常为模型预测的量或是被观察到的估计量。
优点和缺点：RMSD计算简单，但依赖于结构对齐的准确性，对整体结构拓扑的变化不敏感，且对柔性区域的差异敏感。

ϵRMSD：

定义：ϵRMSD是在RMSD的基础上发展起来的一种方法，通过考虑结构中不同部分的灵活性，对柔性区域和刚性区域进行区分。
计算方法：与RMSD类似，但通常只考虑结构中的一部分原子（如骨架原子）进行计算，以减少柔性区域对结果的影响。
应用：在需要更精细地分析结构变化的情况下，如蛋白质-配体复合物的模拟，ϵRMSD可以提供更有价值的信息。
优点和缺点：ϵRMSD能够更准确地反映结构的局部变化，但对柔性区域的处理可能会引入偏差。

十八、TM-score（蛋白质结构相似性）

一种用于评估两个蛋白质结构相似性的指标。它主要考虑的是整体折叠情况的相似性，而非局部结构的相似性。

TM-score的数值在0到1之间，其中1表示两个蛋白质结构完全一致。当TM-score低于0.17时，意味着这两个蛋白质结构是随机选择的，没有关联。而当TM-score大约为0.5时，表示这两个蛋白质结构有相似的折叠情况。

TM-score同样适用于RNA结构的评估。

十九、局部距离差异测试IDDT

局部距离差异测试（Local Distance Difference Test，lDDT）是一种用于评估蛋白质结构预测模型精度的指标。它主要用于比较预测的蛋白质三维结构与参考结构（通常是实验确定的结构，如X射线晶体学或核磁共振结构）之间的局部几何差异。

主要特点和原理：
1. 局部距离计算：
lDDT 的计算基于蛋白质结构中原子之间的局部距离。具体来说，lDDT比较了预测模型和参考结构中每对原子之间的距离。不同于全局对齐方法，lDDT关注局部的几何特征，尤其适用于检测局部区域的结构精度。

2. 不依赖于全局对齐：
传统的结构比较方法（如RMSD，Root-Mean-Square Deviation）通常依赖于全局对齐，而lDDT则不依赖于这种对齐。它直接评估结构中每对原子间的距离，提供了一种对局部误差更加敏感的测量方式。

3. 鲁棒性：
IDDT特别适合评估那些预测模型中存在局部错误或结构多样性的情况，因为它不会因为少数几个远离参考结构的原子位置而受到过度影响。

4. 计算过程：
计算lDDT时，首先选定一个原子为中心，并计算该原子与其周围一定范围内的其他原子的距离差异。然后将这些距离差异与参考结构中的对应差异进行比较，最终计算得到一个归一化的分值，反映了预测结构与参考结构在局部几何形态上的相似程度。

5. 得分解释：
lDDT的得分通常介于0到1之间，其中1表示预测结构与参考结构在局部几何上完全一致，0表示存在显著差异。得分越高，表明预测结构的局部几何精度越高。

应用：
lDDT被广泛应用于蛋白质结构预测领域，特别是在评估深度学习模型生成的蛋白质结构时。它是衡量结构预测模型性能的重要指标之一，尤其在国际著名的蛋白质结构预测竞赛（如CASP）中得到广泛应用。

二十、RNA特定相互作用指数（INF-ALL）

RNA特定相互作用指数（INF-ALL）是一种用于评估RNA三维结构预测中关键相互作用准确性的指标。它综合考虑了Watson-Crick（WC）配对、非Watson-Crick（nWC）配对和堆积（STACK）等RNA特有的相互作用。

具体来说，INF-ALL通过以下方式计算：

Watson-Crick配对（INF-WC）：评估预测结构中Watson-Crick配对的准确性。Watson-Crick配对是RNA中最常见的配对类型，包括A-U和C-G配对。
非Watson-Crick配对（INF-NWC）：评估预测结构中非Watson-Crick配对的准确性。非Watson-Crick配对包括G-U wobble配对和其他不常见的配对类型。
堆积（INF-STACK）：评估预测结构中碱基堆积的准确性。碱基堆积是指一个碱基在另一个碱基上的堆叠，这种相互作用对于RNA的稳定性和功能至关重要。

INF-ALL的计算通常包括以下几个步骤：