融合中异常值剔除方法

​

GNSS Outlier Mitigation via Graduated Non-Convexity Factor Graph Optimization

2022 香港理工

GNC（graduated non-convexity） 渐进非凸性

主要贡献：

基于伪距、多普勒观测建立图优化，自适应权重估计。自适应权重估计是基于non-convex Geman McClure函数和GNC实现。
通过“粗——精处理”，使用GNC，全局估计最佳权重。
​​​​​​​​​​​​​​​​​​
​​​​伪距因子

多普勒因子

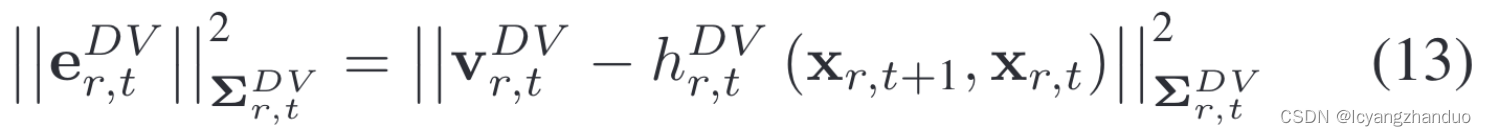
整体误差

GNSS伪距、多普勒outlier识别

Doppler观测受多路径和非视距接受（NLOS reception）的影响相对较小，主要考虑伪距的outlier。因此优化方程变为如下，其中Ψ()为鲁棒函数。

根据 Black-Rangarajan Duality，鲁棒的非线性最小二乘问题等价于如下
ω_t,s表示卫星s在t时刻伪距的权重，在【0，1】区间。
Φ_ρ(ω_t,s)函数是outlier处理，作为权重的惩罚。
上式中，x和权重是要求解的变量。
使用Geman McClure函数，加权的伪距误差等价于

cGM是决定Geman McClure函数*形状的参数。

Geman McClure函数为非凸函数，有陷入局部最小值的问题。GNC方法可以用来解决该问题，如下所示，增加了参数θ。

θ比较大时，此函数变为凸函数，可以解决全局唯一解问题；为1时，又变成Geman McClure函数，可以消除outlier的影响。因此使用θ按照从大到小的顺序，通过多次迭代，每次迭代的结果作为下次迭代的初值，类似于从粗到精的优化。

16式变为如下形式

权重惩罚函数为


θ的初始值按照下式选择，保证首次把所有的观测的餐叉都在凸函数区域。然后按照1.4的比例缩小，直到θ小于1。


通常融合定位有一个相对来说比较好的初始值，是否可以只用GM损失函数？

https://blog.csdn.net/a13956621590/article/details/116033795
https://blog.csdn.net/weixin_43118645/article/details/114544456 以点云配准为例的博客
https://zhuanlan.zhihu.com/p/269230840

点云拼接、配准算法 Fast globel Registration

fast globel registration用于缝合部分重叠的点云。
优化目标为

ρ为一个优化激活函数称为：Geman-McClure。
，以Geman-McClure为核函数的话，目标函数优化比较困难，所以利用Black-Rangarajan duality定理对目标函数进行等价变换


在使用中应该是交替优化T和L，其中L代表{Lp,q}过程如下：

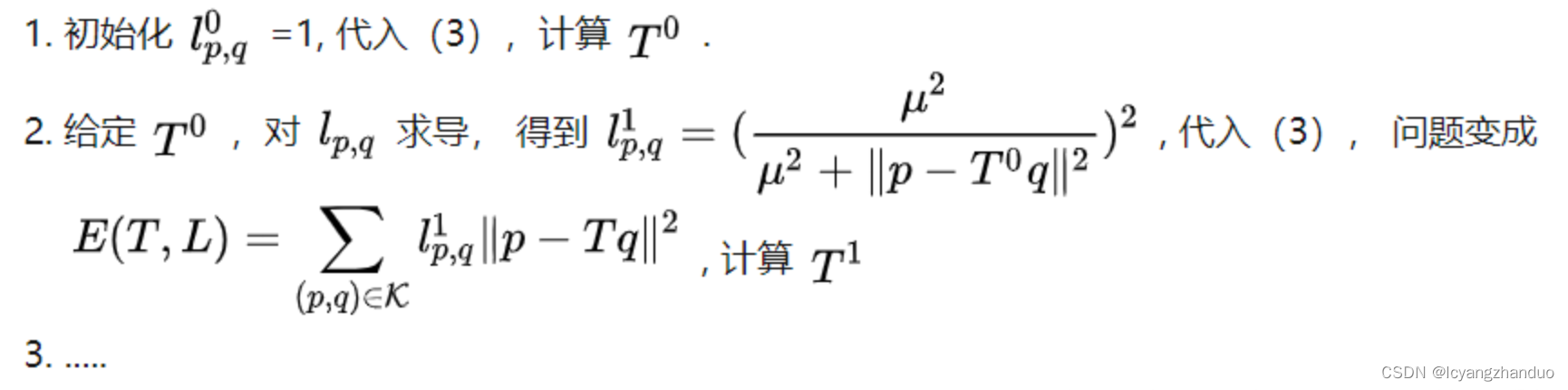
Graduated Non-Convexity (GNC)是一般非凸代价函数ρ(·)的一种常用优化方法。

​