Batch Normalization 学习笔记

最新推荐文章于 2024-04-08 11:15:14 发布

AI莉莉兹

最新推荐文章于 2024-04-08 11:15:14 发布

阅读量1.2w

点赞数 10

分类专栏：机器学习/深度学习 CS231n 文章标签：深度学习

本文链接：https://blog.csdn.net/leayc/article/details/77645877

版权

机器学习/深度学习同时被 2 个专栏收录

21 篇文章 1 订阅

订阅专栏

CS231n

2 篇文章 0 订阅

订阅专栏

前置阅读

[1]. 论文原文. https://arxiv.org/abs/1502.03167
[3]. 深度学习中 Batch Normalization为什么效果好？ - 回答作者: 魏秀参. https://zhihu.com/question/38102762/answer/85238569
[9]. 从Bayesian角度浅析Batch Normalization. http://www.cnblogs.com/neopenx/p/5211969.html

Batch Normalization （以下简称为 BN ）来自两位 Google 研究员发表的一篇重要论文[1] ，中文一般翻译为“批标准化/规范化”。其核心思想是，在深度网络的中间层内添加正态标准化处理（作为 BN 层出现），同时约束网络在训练过程中自动调整该标准化的强度，从而加快训练速度并降低权值初始化的成本。
BN 对于设计更深层网络有一定的帮助。Kaiming He et al. 的 ResNet 最深达到了152层，其中就添加有大量的 BN 层。
BN 现在已经成为了重要的 tricks 之一。
另根据 Google Scholar 的统计，截至本文写作时，该文的引用数已经超过了2000，已经成为 Deep Learning 领域相当重要的文章了。

本文是一篇学习 BN 的总结性笔记，将作为小组学习的参考材料。由于笔者才疏学浅，学习和写作过程中又“剽窃”了许多其他文章和资料（见Ref.），本文的严谨性难以得到保证。故仅供参考，欢迎批评指正。

I. A framework of the original paper

首先来梳理一下原论文的内容。

i. Introduction: 讲了训练深度网络时的几个重要问题，如 learning rate 的选择、参数的初始化需要非常小心；随着网络层数加深，值在层间的传递情况变得非常复杂，初期的微动在网络深处可能造成极大的影响；前人所做的工作，如使用新的 ReLU 激活函数、新的初始化方法 Xavier 等。
ii. Towards Reducing Internal Covariate Shift: 主要把 1. 中的问题概括为 ICS 的概念，介绍了一些相关工作和作者对此的思考。
iii. Normalization via Mini-Batch Statistics: 详细解释了 BN 的算法。
iv. Experiments: 针对前文提出的问题所做的实验。值得注意的是，由于 BN 加速了网络的训练， ensemble 方法的成本得以降低。所以作者最后使用了结合 BN 的 Inception ensemble 模型，实现了当时最优的 top-5 error 。

接下来将按照为什么、是什么、怎么做的顺序来对 BN 做一个重述。
其中“为什么”是重点。后两部分因为思路比较清晰，可以结合自己的情况去学习。

II. The reasons of doing BN

虽然论文中强调的是 ICS，但笔者认为梯度消失/爆炸是个更好的角度。

i. Internal Covariate Shift

作者们在论文中特别介绍了 Internal Covariate Shift (ICS) 的概念。这个概念是对 Covariate Shift 的引申。按照文中的说法，“当一个学习系统的输入的分布发生改变时，就发生了所谓的 Covariate Shift[2]”。对这个概念，[3]解释得很清楚。
这里笔者再从迁移学习的角度做一点补充。[4]

迁移学习中有这样一对基本概念： $domain$ 和 $task$ 。
$domain$ 包含特征空间 $\mathcal{X}$ 和边缘概率分布 $P(X)$ , 其中 $X = \{x_1, x_2, ...x_n\} \in \mathcal{X}$ 。所以一个 $domain$ $D$ 就可以表示为 $D = \{ \mathcal{X}, P(X)\}$ 。而如果说两个 $domain$ 不相同，则可能是它们的特征空间 $\mathcal{X}$ 不同，或者边缘概率分布 $P(X)$ 不同。
给定一个 $domain$ $D$ 时， $task$ 也由两部分组成：标签空间 $\mathcal{Y}$ 和目标预测函数 $f(·)$ 。 $f(·)$ 是从训练数据对 $\{x_i, y_i\}$ 学习得到的。所以可以写作 $\mathcal{T} = \{\mathcal{Y}, f(·)\}$ 。其中，如果概率的角度考虑， $f(·)$ 也可以写作 $P(y|x)$ 。

考虑两组不同 $domain$ 的数据 —— 源 $domain$ 数据 $D_S = \{({x_S}_1, {y_S}_1), ... , ({{{x_S}_n}_s}, {{y_S}_n}_s) \}$ 和目标 $domain$ 数据 $D_T = \{({x_T}_1, {y_T}_1), ... , ({{x_T}_n}_s, {{y_T}_n}_s)\}$ ，通常 $0 \le n_T \ll n_S$ ——给定源 $domain$ $D_S$ 和学习 $task$ $T_S$ ，目标空间 $D_T$ 和 $task$ $T_T$ ，当 $D_S \neq D_T$ 或 $T_S \neq T_T$ 时，一个一般意义上的迁移学习问题就可以定义为：从 $D_S$ 和 $T_S$ 中学习知识，以改善目标预测函数 $f_T(·)$ 。
不难看出，当 $D_S = D_T$ 、 $T_S = T_T$ 时，该问题就退化为一个普通的机器学习问题。

源 $domain$ 与目标 $domain$ 不同、但源 $task$ 与目标 $task$ 相同时，这类任务称为 transductive learning。由于 $\mathcal{X} = \{\mathcal{X}, P(X)\}$ ，两 $domain$ 不相同可能是 $\mathcal(X)$ 不同，也可能是 $P(X)$ 不同。一些迁移学习问题如 domain adaption for knowledge transfer，sample selection bias 或者 covariate shift 就属于 $P(X)$ 不同的情况。
这样就与源论文中的 “When the input distribution to a learning system changes, it is said to experience covariate shift.” 联系起来了。

然后加上所谓的 “Internal”，参考[3]也就好理解了。不加 “Internal”，说的是整个系统的输入发生变化；加上 “Internal”，指的就是在系统——深度网络内部的层与层之间发生的变化，也就是论文在 I、II 部分所解释的内容。

ii. Gradient Vanishing/Exploding

众所周知，深度学习的浪潮始于2006年 Hinton 的文章，但直到 2012 年他和学生 Alex 用 AlexNet 爆掉其他人的传统 CV 方法、以及 Andrew Ng. 在 Google 做出了能从图像数据中自学习到“猫”的概念的 Google Brain 之前，学术界和工业界大部分人都没有把 Deep Neural Networks 当回事。
而如果继续回溯源头，多层神经网络、卷积神经网络、长短时记忆这些框架更是早已有之。深度学习直到 2012 年之后才获得爆发式的发展，原因大多被总结为大数据和并行计算两方面的进步。
然而，如果从神经网络的结构本身来考虑，其实一个最主要的问题在于：
深度网络难以训练。

训练深度网络的常规方法是 backpropagation 指导下的随机梯度下降（stochastic gradient descent）。这套方法通常行之有效，但对于缺乏经验的使用者而言，失效的情况却更多一些。
原因很简单。网络的一般训练过程是这样的：

(1) 初始化参数空间 W
(2) 输入数据，forward passing
(3) 返回 loss 、back-propagating 各层的梯度并更新权值
重复(2)(3)直到结果收敛

假设输入数据的范围是 (0, 1)，初始化参数为0.01*正态分布，非线性函数使用 tanh ——这是过去的常用配置之一。观察 forward passing 的结果。
代码见[5]。
(该部分内容参考了 Stanford CS231n [6]。)

容易看到，在级联结构的作用下，由于初始权重较小，输入数值在逐层传递的过程中逐渐收缩，最后都成了0。
将初始化权值去掉0.01系数，后续数值就变成了

反向传播阶段的情形与之类似。这就产生了所谓的梯度消失/爆炸问题。
换成 sigmoid 函数也一样。其导数 $\sigma' = \sigma * (1-\sigma)$ ，最大值出现在 $\sigma(0) = 0.5$ 时， $\sigma'(0) = 0.25 \ll 1$ ，因而每经过一层，梯度都会收缩。小梯度降低了学习的速度，甚至导致网络无法学习。
所以为了“安全”地训练一个网络，我们自然而然地就会希望，数值在层间传递时，能够稳定在一个大概的范围内——既不要太大，也不要太小：
比如单位高斯（unit Gaussian） $N(0, 1)$ 就是极好的。
比如单位高斯（unit Gaussian） $N(0, 1)$ 就是极好的。
比如单位高斯（unit Gaussian） $N(0, 1)$ 就是极好的。

再考虑随机梯度下降的计算过程。

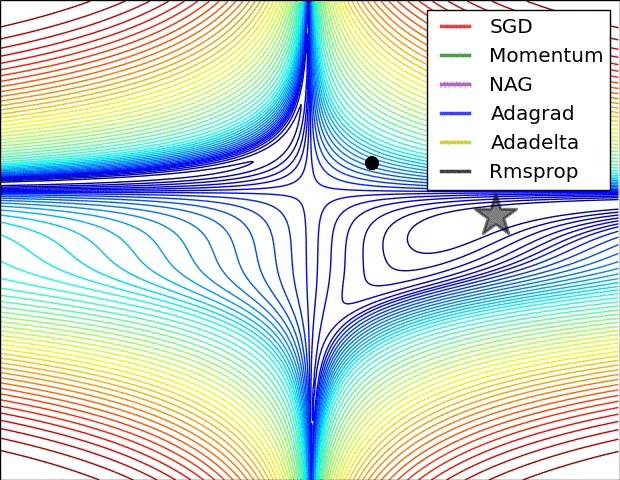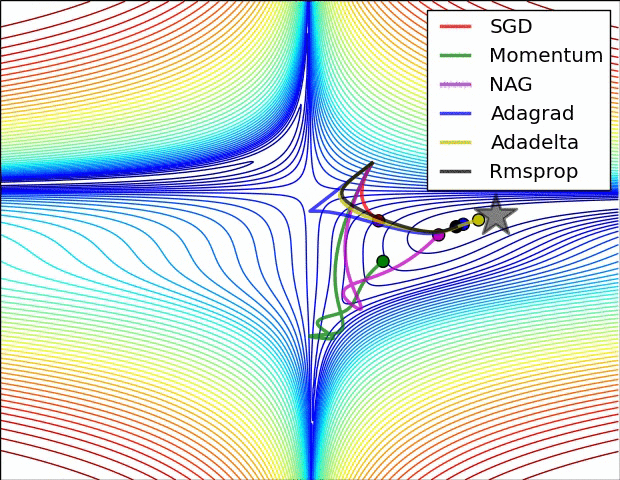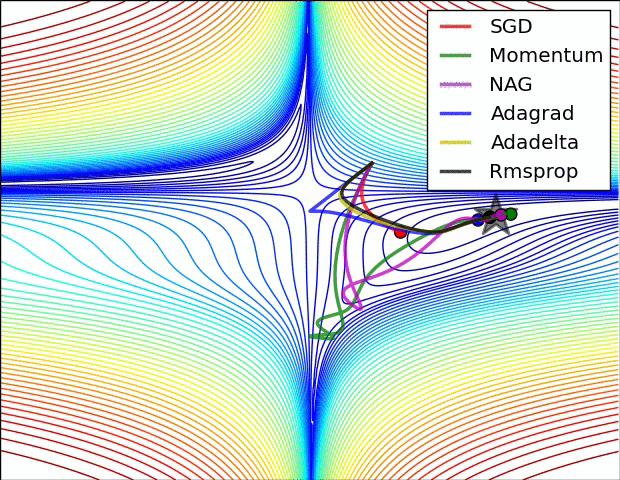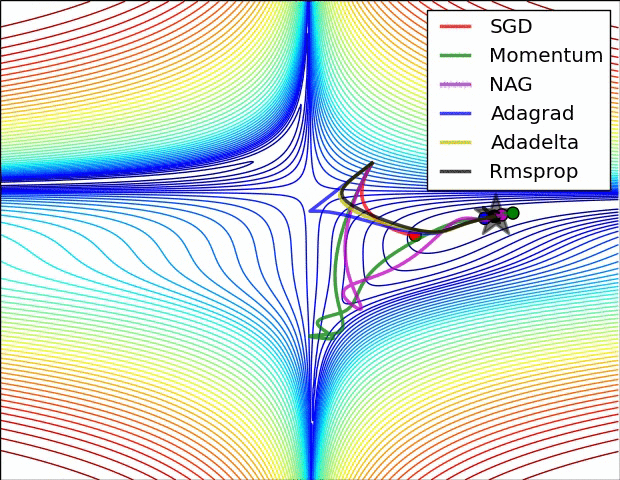
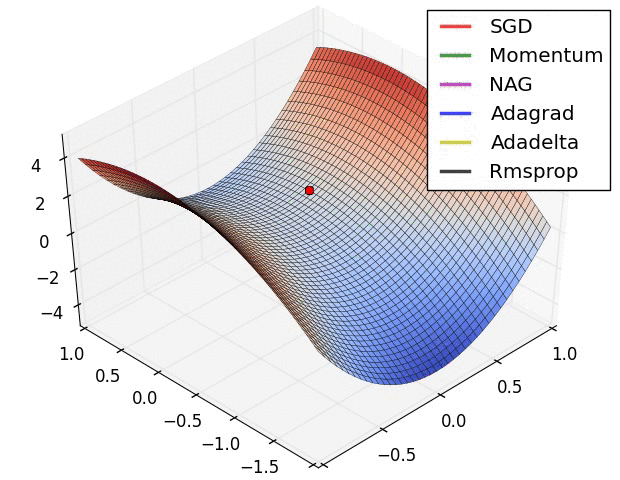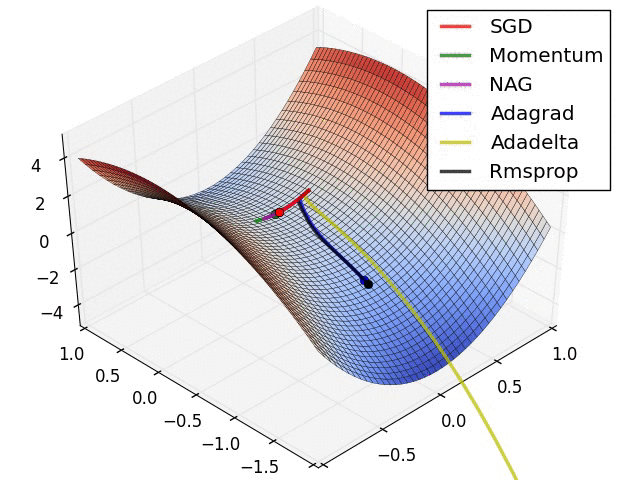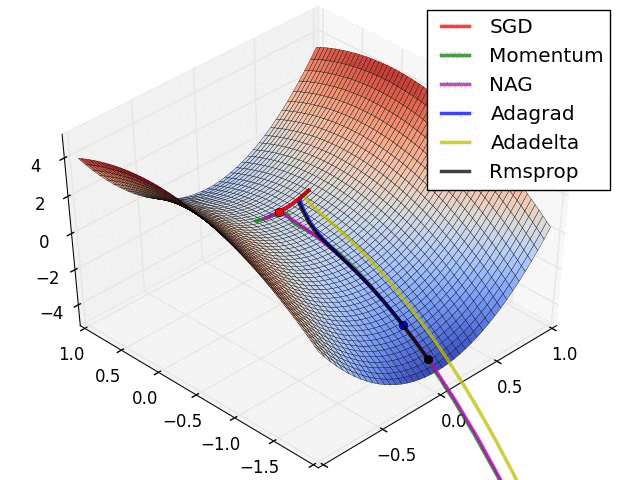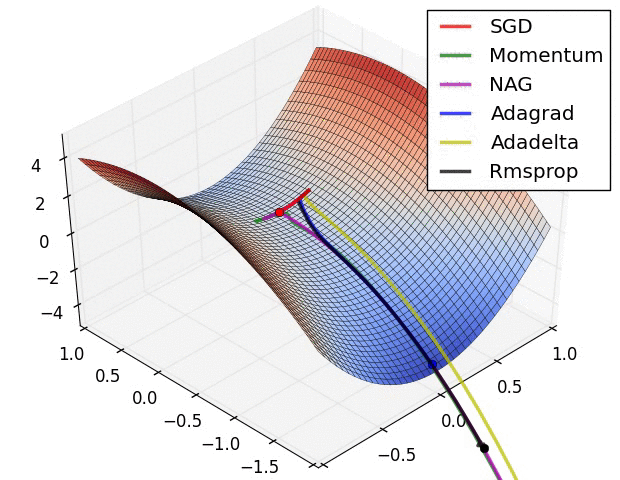
图自[6]

我们知道，在训练网络时，超参数 learning rate （学习率）的选择也非常关键。过大的学习率容易妨碍收敛，过小的学习率降低学习速度，而且容易被困在鞍点或较差的极小值处。

所以，深度网络需要更合理的初始化策略，更合适的非线性激活函数，以及选择 learning rate 的更优策略。
权值初始化是深度学习比较重要的一个研究方向，可以参考2017 spring 版 CS231n 课程中的相关部分[6]；激活函数方面， ReLU (=max(0, x)) 单元的发明则非常关键：通过放开对 activations 正值部分的限制，让数值在传播过程中不至于湮灭。另外在优化方法上，Rmsprop、Adam 等二阶算法也已经非常流行了。
选择 learning rate 常用的方法是随机网格搜索：在对数网格中选择结果较好的数值，接着缩小范围继续搜索，从而确定最佳学习率。

再考虑另一个问题。

iii. Normalization

这里写图片描述
图片来自[6].
做过机器学习的朋友可能都知道，数据预处理阶段经常要做所谓的（按维度）归一化/标准化。归一化的作用，简单来说，就是避免特征向量中一部分特征的数值过大/过小，导致算法错误地分配权值。

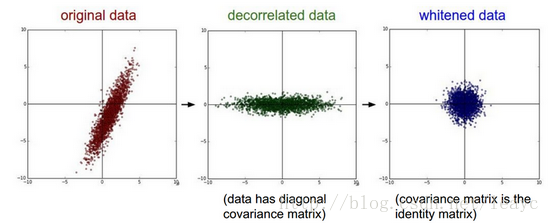
这里写图片描述
类似地，有时还会对数据做白化操作。
不过一般来说，深度学习在图像任务中通常只做中心化平移（减均值），而不考虑尺度变化。

那如果做了全套的正态标准化，会出现什么结果呢？

iv. Batch Normalization

对输入和中间层做标准化并不新鲜，原文提过之前的一些工作，同年还有一篇与 BN 很相似的文章《Spatial Transformer Networks》。前人的遗憾在于，没有将“中间层标准化”有机地结合到网络当中去。
不信的话，可以不用 BN 文章的思路，按照自己的想法去做逐层标准化处理。
结果大概率是乱七八糟的。

综合本节内容不难看出，ICS 和 gradient vanishing 其实是同一个问题的两个截面。讲法虽然不同，指向的实际问题却是一致的。
所以问题早就明确了，全看大家的解决方案好不好用。

III. What Batch Normalization is

描述 BN ，最简单的形容还是 CS231n 里的：You want unit Gaussian activations? Just make them so.
还是从 sigmoid 函数出发：
这里写图片描述
（图自wikipedia）

由于S 函数是以0为中心的非线性映射，我们希望 S 函数的输入也是以0为中心的，故进行 BN 操作的时机就在 $WX + b$ 之后。而 BN 操作本身要做平移，所以 $b$ 也可以省掉了。

i. Forward passing

公式很简单：

μ B = 1 B \sum i B μ i ， σ 2 B = 1 B - 1 \sum i B σ 2 i ， X^= X - μ B σ 2 B + ϵ - - - - - \sqrt

$\mu_B = \frac{1}{B} \sum_i^B \mu_i ，\\ \sigma_B^2 = \frac{1}{B - 1} \sum_i^B \sigma^2_i ，\\ \hat{X} = \frac{X - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}\$
需要注意，为了减小计算量，均值和方差的计算都是在单维度上进行；而对于卷积神经网络，就需要在 channel 维上对矩阵做运算。CS231n 的作业中讲得很清楚[8]。
做完 BN 之后，还需要将其“还原”：

y = γ X^+ β

$y = \gamma \hat{X} + \beta$

其中， $\gamma 、 \beta$ 是自适应的参数，通常设定初始值 $\beta \approx 0 、\gamma \approx 1$ ，在反向传播过程中随同其他参数一起参与训练。容易发现当 $\beta = \mu_B 、 \gamma = \sigma_B^2$ 时， BN 操作就被抵消了。这是考虑到虽然将 activations 做了标准化处理，但是对网络来说，我们无法知道这样的操作对于学习有无益处。对这一点，潘神的博客讲得极好[9]，推荐认真阅读。

ii. Backpropagation with BN

直接贴公式：
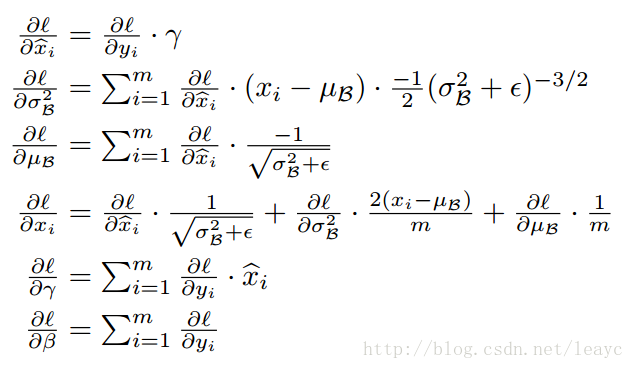
这里写图片描述
推导使用了链式法则和多元函数求导的知识。详细过程可以参考[10]。
注意到上述公式是直接使用链式法则推得的。可以将各式充分展开、消元后得到新的公式。由于省去了一部分中间过程，在编写代码时可以提高速度。这一点 CS231n 的作业中有所体现，使用小规模随机数测试，展开后公式的写法速度为原公式写法的1.5~2+倍。
推导过程也可以参考[11]。

iii. Different behaviors in training and testing

训练阶段，标准化在每个 mini-batch 上操作，但测试阶段， $\mu_B、\sigma_B^2、\beta、\gamma$ 均使用固定值。这部分可以参考[9][10]和下一节提供的代码链接。

IV. How to do Batch Normalization

具体的代码编写有多种版本，可以参考：

[8]： CS231n 的课程作业；
[7]：基于 Tensorflow 的一个 BN 教程；
[12]： Tensorflow 的官方文档；
[13]：基于 Caffe 的一个 BN 实现，思路可参考 [9] 中的解说。

V. Discussion

知乎问题 [3] 以及文章 [14] 还有一些相关的讨论。
本文提到的内容并非 BN 全貌，实践中还存在许多问题尚未解决。 BN 只是“减轻”了梯度消失的症状而非彻底解决，在设计深层网络时，学习率的选择、权值初始化仍然困难重重。比如 RNN 的 BN 该怎么做？有没有更好的标准化策略？仍有待进一步研究。

接下来的内容是学习 BN 前后的一些瞎想，与本文主题基本无关，读者大可以跳过。

True improvements made by deep learning

接触一段深度学习之后会发现，这第三次神经网络浪潮里火起来的多数工具并不新鲜。
比如 LSTM 是 1990 年代发明的，用来解决 RNN 的梯度消失/爆炸问题； CNN 是 1980 年代发明的，把它发扬光大的 Yann LeCun 最著名的工作之一，就是 1998 年在手写数字识别问题上实现的 LeNet——2012 年的 AlexNet 的结构与之非常相似；多层神经网络 MLP 完全不是什么新鲜事；就连本文的 BN ，与之类似的 ideas 也是数不过来（说来有趣，连最著名的 backpropagation 真正的最初发明人在业内都是一桩公案）。
那么这次浪潮以及由此推动的第三波 AI 热，到底有没有真正的进步呢？
肯定是有的，但同样需要时间的检验。

神经网络拟合能力之强，很早就被所谓 Universal Approximation Theorem 证明过：输入-隐层-输出的简单三层网络，可以实现对任意函数的拟合。但这种“容量”要求隐层单元数无限多，明显缺少实际意义。
后来，通过使用较少的隐层单元同时增加网络层数，构建所谓的多（深）层网络，研究者实现了“对复杂数据的高层次特征建模”。
深度网络强大的建模能力来自逐层非线性和巨大的参数空间——VGGNet的参数总量达到了138M。在如此巨大的非凸空间上做优化是极端困难的，因而对一阶方法如梯度下降、二阶方法如拟牛顿法还有“死灰复燃”的遗传/进化算法等优化方法的研究，也是深度学习的重要分支之一。
Bengio 组的工作证明，多数情况下局部极小足以应付一般的学习任务，这是一个好消息。

前面说过，很多人认为深度学习的复兴得益于海量数据和并行计算。但与之匹配的新算法的作用，同样不可忽视。
周志华教授、姚期智教授等在接受采访时都曾表示，相对数据、算力的发展来说，算法仍有巨大的进步空间。
数据和算力的提升，让深度神经网络得以重新发挥作用，随之而来的新算法则不断提升了它的效率。就像 BN 的产生，浅层网络可能不需要多此一举，但深达几十几百甚至上千层的网络，不做类似的处理，肯定是无法训练的。
类似的小 tricks 让网络训练更具可行性，而如 GAN 之类的发明，也带来了新的研究思路。

Trade-offs in practice

神经网络似乎经常给人不靠谱的感觉，有一个重要原因是，实践跟理论差别比较大、近似操作做得太多，有些具体的算法甚至难以用理论来解释。相比之下，一些传统的机器学习模型如 SVM 有良好的理论保障，得到的结果也不错，这是神经网络在 1990 年代被 SVM 爆掉的一条主因。

不过，如果从 trade-off 的角度来考虑，很多看起来扯淡的操作似乎就不那么扯淡了。
举几个具体的例子。

Batch gradient descent 是在整个数据集上做优化，但因为数据集往往比较大，无法负担全局统计的成本，所以就有了 stochastic gradient descent 。最原始的 SGD 计算的是单个样本，但样本中都有噪声、单样本很容易造成偏差，于是就有了 mini-batch gradient descent，在随机生成的小批量样本上求平均。
同样是因为成本原因，BN 操作不仅限定在 mini-batch ，而且还得在同维度上计算。
BN 做完标准化之后要做一次“还原”，因为“无法确定这是不是神经网络自己想要的”——听起来非常喜感，但是这一步非常关键。[9]从贝叶斯的角度做了精彩的解释，作者认为，还原的操作“将normalize的 $\hat{X}$ 逆转回去，是为了在加速收敛和表征破坏之间，留一个trade off的空间”。
- “加速收敛”指的是通过约束 activations 的数值，让参数及其导数在传递中保持比较平稳的状态，从而允许了较大的学习率。
- “表征破坏”指的是，人家好好地传了几层数值，说不定包含了图像的重要特征，结果你强行给人“高斯”了，高斯出来是啥玩意儿谁也没数。
- 所以从优化的角度来看，BN 层希望在训练过程中经过这一来一回，找到一个好的平衡点。
如果对生成模型有所了解，你可能知道受限玻尔兹曼机 RBM 就是对玻尔兹曼机 BM 模型的简化，RBM 的学习算法 CD-1 是对近无穷 CD 的简化，使用 CD-1 的 DBN 是对 SBN 的简化——如果不简化，这些模型是无法计算的。
CNN 中 filter 的大小设定也比较玄乎： 1*1、3*3、5*5、7*7 这些数究竟有什么道理？
……

类似的情况在代码实现和工程实践中体现得更多。虽然看上去好像没有理论保证，但实际效果却往往令人惊讶。所以 trade-off 并不可怕。鉴于神经网络这种实践在理论之前的特性，许多研究者的解释看起来就颇有“马后炮”的意味（像 ICS 就有点生造的意思）。这也是神经网络非常有趣的一点。
文章 [9] 中也多次强调， Deep Learning 的许多操作背后都有 Bayesian Learning 的味道，说 Hinton 学派在算命是不负责任的说法。因此也有人认为，随着 Deep Learning 研究进展越来越深，Bayesian Learning 和 Reinforcement Learning 将迎来万众瞩目的回归。