摘要:城市轨道交通车站客流特征与其周边建成环境和社会经济因素密切相关, 且不同影响因素对客流特征的影响也存在时间和空间异质性。以车站工作日日均客流量、工作日特殊时段(如早高峰进站、早高峰出站、晚高峰进站和晚高峰出站)客流量为因变量, 从车站属性、连接性和建成环境3个方面选择23个自变量, 采用多尺度地理加权回归(MGWR)模型构建客流特征分析模型, 分析不同时间尺度下轨道交通车站客流量的影响因素及其相互作用, 并以南京市轨道交通系统进行实例分析。结果表明:与普通最小二乘法(OLS)回归模型和地理加权回归(GWR)模型相比, MGWR模型更为可靠; 忽略早晚高峰客流影响的全天客流量预测模型拥有的显著自变量最多, 到市中心的距离对客流量有显著的负影响, 证明距离市中心越近的车站的客流量集聚性越明显; 周边居住、生活类设施占比较高的车站对早高峰进站和晚高峰出站客流有很强的吸引作用, 而周边居住、生活类设施占比不高的车站对早高峰出站和晚高峰进站客流有很强的吸引作用。研究结果可以为城市规划部门促进城市轨道交通与城市建设的协同发展提供理论支撑。
传统的城市轨道交通车站客流特征及影响因素研究普遍依赖实地调研、交通调查、统计资料数据,数据的调查和获取通常需要耗费大量的时间、人力和物力成本,且数据的更新频率较低,难以保证研究的准确、全面和实时性。随着城市轨道交通自动售检票系统(automatic fare collection system,AFC)的广泛应用以及信息技术的不断发展,推动了城市轨道交通研究方法及数据由单一向多样化转变。同时,兴趣点(points of interest,POI)数据、开放地图(open street map,OSM)等大数据以及来自商业服务网站、政府部门的开放数据共同促进了大数据时代的到来与新数据环境的形成。与传统数据相比,大数据具有覆盖面广、数据精度高和动态实时更新等优势,对于以上多源异构数据的融合处理与分析,更能反映城市轨道交通与城市空间布局的真实情况[1]。因此,以多源异构数据为基础,研究城市轨道交通车站客流特征影响机理,有助于理解城市轨道交通出行的内在机理和城市空间格局的演化规律,为城市轨道交通与城市建设的协同发展提供理论支持。
在城市轨道交通车站客流影响机理的研究中,现有研究主要集中在影响因素选取和回归模型选择2方面。
从城市轨道交通车站客流特征影响因素的选取上来看,研究者尝试从多角度选取车站客流特征的影响因素,大致可以归纳总结为车站自身属性、连接性指标、建成环境指标3类。其中,车站自身属性包括是否为换乘站、是否为端点站、是否位于中央商务区(central business district, CBD)和车站经过的轨道交通线路数量;连接性指标包括车站与市中心的距离、车站服务范围内停车场数量和接驳公交线路数量;建成环境指标包括车站服务范围内的人口数量和建筑面积。Kuby等[2]认为是否为端点站、是否为换乘站、停车换乘车位数量、接驳公交线路数量、车站服务范围内的居住人口和就业人口数量等对城市轨道交通车站工作日日均客流量有显著影响;Sohn等[3]发现是否为换乘站、接驳公交线路数量、平均换乘次数、车站服务范围内的人口数量和建筑面积等对城市轨道交通车站工作日日均客流量有显著影响;Loo等[4]认为是否为换乘站、到市中心的出行费用、车站服务范围内的商业建筑面积和人口数量对城市轨道交通车站工作日日均客流量有显著影响;Zhao等[5]在上述研究的基础上,结合中国城市轨道交通车站站域的布局特点,首次考虑了自行车停车换乘空间这个影响因素,结果发现:自行车停车换乘空间也对轨道交通车站工作日日均客流量有显著影响;岂常禄等[6]考虑了轨道交通车站周边土地开发的复杂性,将用地类型分为居住、办公、购物、医疗和教育5类,采用土地利用混合度综合反映车站周边土地利用程度;Wang等[7]进一步细化建成环境影响因素,选择餐饮购物、文化教育、医疗服务和旅游景点的POI数量作为自变量。
从城市轨道交通车站客流特征建模方法来看,主要经历了3个阶段。初期研究主要采用普通最小二乘法(ordinary least squares,OLS)回归模型[2, 4, 8-9]。但是,OLS回归模型存在一个明显的缺陷,即模型假设各观测值之间都是相互独立的,且在空间上是同质的。然而,国内外的大量研究和实践表明,包括城市轨道交通车站覆盖范围在内的城市各个区域并不是一直静止不变的,而是不断发展变化;且各区域的土地利用性质也不是同质的,而是在空间上存在相互依赖性和互补性[10]。因此,部分学者认识到将空间位置因素嵌入到回归系数中的地理加权回归(geographically weighted regression,GWR)模型不仅拟合能力优异,而且还克服了OLS回归模型无法描述空间指标的局限性,能准确反映各个影响因素的作用程度在空间上的分布差异[11-12],并分别对马德里[13]、南京[14]和西安[15]等城市轨道交通车站进行实证分析。尽管考虑空间异质性的GWR模型比传统的OLS回归模型具有更好的拟合优度,但有学者指出,GWR模型同样存在一些不足,即只考虑了影响因素的局部作用差异,而忽略了某些变量的影响作用在空间上可能是平稳的这一事实[16]。基于此,一些学者提出一种将OLS和GWR相结合的多尺度地理加权回归(multiscale geographically weighted regression, MGWR)模型,采用MGWR模型分析建成环境对城市轨道交通车站客流特征的影响机理。Jun等[17]采用MGWR模型研究了首尔市轨道交通车站客流的影响机理;Chen等[18]分别采用OLS回归、GWR和MGWR模型研究福冈市轨道交通车站客流的影响机理;高德辉等[19]采用MGWR模型研究北京市轨道交通车站客流的影响机理。
综上所述,现有研究在影响因素选取和回归模型选择已经取得了一定的成果,但仍有进一步深入探讨的必要,主要体现在以下2个方面:一是建成环境指标的划分不够详细,鲜有研究同时考虑车站周边不同设施的密度和建筑面积;二是现有研究大多以车站工作日日均客流量为因变量,没有考虑车站客流量在一天中的波动特性,即高峰时段客流的集聚性分布,同时也没有考虑进出站客流的潮汐特性。
为了客观、准确地刻画城市轨道交通车站工作日客流特征的影响机理,本文以2017年9月南京市轨道交通系统连续两周的进出站客流数据为基础,以车站工作日日均客流量、工作日特殊时段(如早高峰进站、早高峰出站、晚高峰进站和晚高峰出站)客流量为因变量,从车站属性、连接性和建成环境3个方面选择自变量,采用MGWR模型构建客流特征分析模型,分析不同时间尺度下轨道交通车站客流量的影响因素及其作用机理。
1 研究方法与模型构建1.1 指标共线性与空间自相关检验
目前,最常用的共线性检验指标是方差膨胀系数(variance inflation factor, VIF),该指标为回归系数估计值的方差与假设自变量间非线性相关时方差的比值[20]。第l个自变量el的方差膨胀系数为
| $ \mathrm{VIF}_{l}=\frac{1}{1-R_{l}^{2}} \text {. } $ | (1) |
其中:VIFl为第l个自变量的方差膨胀系数;Rl2为把el看作因变量,用其余自变量作线性回归得到的决定系数。
可见,VIFl的值越大,表明el与其他变量之间存在共线性的概率越大,一般可以接受的方差膨胀系数取值在10以内。
此外,本文采用Moran指数研究变量间的空间自相关检验。Moran′I是用来度量空间自相关常用的全局指标,反映某一指标在空间邻近的区域单元内的相似程度[21]。则el的全局Moran指数计算公式为
| $ \operatorname{Moran}^{\prime} \mathrm{I}_l=\frac{\sum\limits_{i=1}^m \sum\limits_{j=1}^m \gamma_{i j}\left(e_{i l}-\bar{e}_l\right)\left(e_{j l}-\bar{e}_l\right)}{S_l^2 \sum\limits_{i=1}^m \sum\limits_{j=1}^m \gamma_{i j}} . $ | (2) |
其中:Moran′Il为el的全局Moran指数;m为轨道交通车站的数量;γij为车站i和j之间的权重取值;eil为el在第i个车站的观测值;ejl为el在第j个车站的观测值;el为el在所有车站的均值;Sl2为el在所有车站的方差。
Moran′I的取值一般为[-1, 1]。在给定的显著性检验水平内,Moran′I等于0时表示不存在空间自相关,大于0时表示变量在空间上呈现聚集状态(空间正相关),小于0表示变量在空间上呈分散状态(空间负相关)。通常采用标准化统计量Z值进行显著性检验,计算公式为[22]
| $ Z\left(\text {Moran}^{\prime} \mathrm{I}\right)=\frac{\operatorname{Moran}^{\prime} \mathrm{I}-E\left(\operatorname{Moran}^{\prime} \mathrm{I}\right)}{\sqrt{\operatorname{Var}\left(\operatorname{Moran}^{\prime} \mathrm{I}\right)}} . $ | (3) |
其中E(Moran′I)和Var(Moran′I)分别为Moran′I的理论数学期望和理论方差。
1.2 地理加权回归及其改进模型
OLS回归模型是一种常用的研究因变量和自变量之间相关关系的统计模型,其最明显的不足在于假设因变量与自变量之间的关系为全局关系。GWR模型是在传统的OLS回归模型基础上结合了空间权重等信息,将变量的地理空间分布位置考虑在回归参数内的回归模型[23]。对于第i个城市轨道交通车站的客流量Fi,GWR模型公式为
| $ F_{i}=\beta_{0}\left(\mu_{i}, v_{i}\right)+\sum\limits_{l=1}^{n} \beta_{l}\left(\mu_{i}, v_{i}\right) e_{l}+\varepsilon_{i} . $ | (4) |
其中:(μi, νi)为车站i的空间位置,其中μi和νi分别为车站i的经度和纬度;β0(μi, νi)为(μi, νi)处的截距;n为自变量的数量;βl(μi, νi)为el在(μi, νi)处的回归系数;εi为车站i的模型残差。
GWR模型的空间权重的确定也要遵循空间区域之间的邻近关系,即邻近车站的空间权重大于远离车站的。GWR模型是局部回归模型,因此需要一个带宽指数作为变量来确定局部回归之间的影响。若带宽设置过大时,整个分析区域内的车站均为邻近车站,此时的回归过程就变成了全局回归;反之,整个分析区域内的车站是相互独立的,即所有车站的指标都具有独立性。可见,带宽的设置对于GWR模型的求解有着重要的影响。通常情况下,采用校正AIC值(AICc)来确定带宽的设置。
MGWR模型是GWR模型的拓展和延伸,同时考虑了自变量中的全局指标和局部指标[24],克服了GWR模型中变量影响作用的空间非平稳性问题。分别采用不同的带宽求解不同的自变量指标,以准确反映不同参数估计对应的异质性尺度特征。对于Fi,MGWR模型公式为
| $ F_{i}=\beta_{0}\left(\mu_{i}, \nu_{i}\right)+\sum\limits_{l=1}^{k} \beta_{l} e_{l}+\sum\limits_{l=k+1}^{n} \beta_{l}\left(\mu_{i}, \nu_{i}\right) e_{l}+\varepsilon_{i} . $ | (5) |
其中k为全局自变量的数量。
由式(5)可知,MGWR模型是OLS回归模型和GWR模型的组合,前k项指标为全局变量,第(k+1)到n项指标为局部变量。MGWR模型选择Gauss函数作为核函数,带宽的设置方法为AICc准则。
1.3 模型检验
回归模型结果的检验主要包括残差平方和(residual sum of squares, RSS)、调整R2即Radj2和AICc 3个评价指标。
RSS指标可以描述实际值和回归预测值之间的偏差程度,反映了模型的预测精度[25],其值越小代表预测精度越高,其计算公式为
| $ \mathrm{RSS}=\sum\limits_{i=1}^{m} \varepsilon_{i}^{2}=\sum\limits_{i=1}^{m}\left(F_{i}-\hat{F}_{i}\right)^{2} . $ | (6) |
其中:RSS为残差平方和;$\hat{F}_i$为第i个车站的预测客流量。
Radj2是在R2的基础上考虑了模型复杂度,计算公式为
| $ R_{\text {adj }}^{2}=1-\frac{\left(1-R^{2}\right)(m-1)}{(m-n-1)} . $ | (7) |
Radj2的取值为[0, 1],其值越接近1,表明回归结果对实际值的拟合程度越好。
AICc综合反映了回归模型结果的GOF和模型的复杂度,计算公式为
| $ \mathrm{AICc}=\mathrm{AIC}+\frac{2 n(n+1)}{m-n-1} . $ | (8) |
AICc取值的变化大于3时,一般可认为模型结果之间存在显著差异[26]。需要注意的是,RSS和AICc指标是针对特定建模过程的相对统计量,即对同一数据集和因变量指标才具有可比性。
2 研究区域与数据2.1 研究区域
南京市是江苏省省会、副省级城市、南京都市圈核心城市,也是中国重要的科研教育基地和综合交通枢纽。南京市第一条轨道交通线路于2005年9月3日正式运营,是中国大陆第6个开通轨道交通的城市。截至2017年9月,南京市共有7条轨道交通线路,分别为1号线、2号线、3号线、4号线、10号线、S1机场线、S8宁天线,共计128座站点(10个换乘站和118个普通站),运营线路总长259 km,涵盖了除溧水区和高淳区外所有的市辖区,如图 1所示。
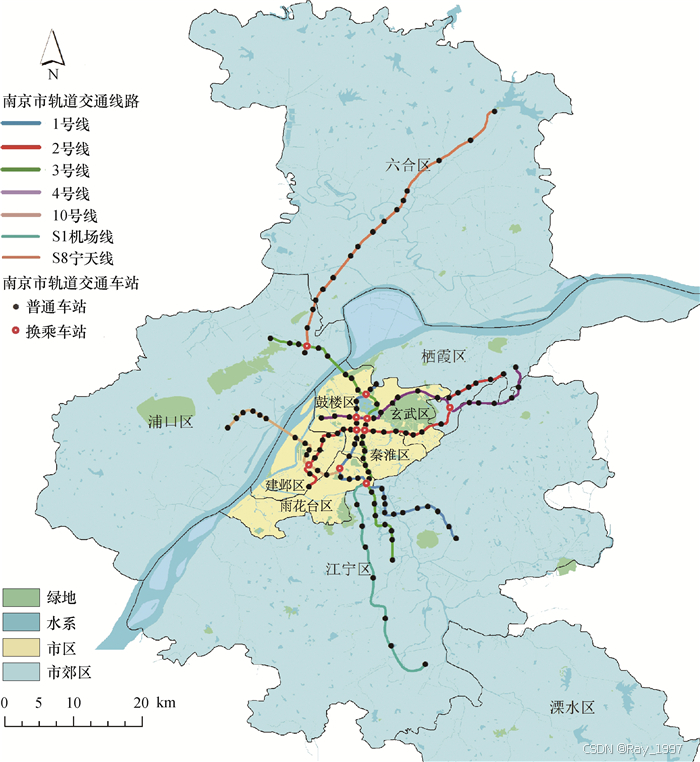 |
| 注:基于国家测绘地理信息局标准地图服务网站标准地图[GS(2016)1589号]制作图 1 2017年南京市轨道交通运营线路 |
2.2 数据采集与预处理
城市轨道交通车站不是孤立存在的,而是有一定的服务范围。现有研究多以轨道交通车站800 m半径范围内覆盖的区域作为车站服务范围[27, 28],因此本文也选择轨道交通车站800 m半径范围内覆盖的区域为车站服务范围。
以2017年南京市轨道交通系统为研究对象,使用的数据包括轨道交通进出站刷卡数据、车站服务范围内的POI数据、车站服务范围内的交通基础设施数据和车站服务范围内的土地利用数据。具体数据内容及处理过程如下:
1) 2017年9月18—22日、9月25—29日南京地铁连续2周的工作日的进出站刷卡数据。通过匹配智能卡卡号信息,将乘客完整的一次进站和出站刷卡过程合并为一条单独的出行记录,可以得到1 669万条出行记录,工作日日均进出站次数为167万人次。
2) 2017年南京市POI数据。本研究通过高德地图开放平台的API接口采用Python爬虫技术获得2017年南京市POI数据32.01万条,并将其分为居住生活类、企业办公类、购物服务类、文化体育类、医疗服务类和旅游观光类6种。
3) 2017年南京市交通基础设施数据。南京市2017年道路网、公交线路和公交站点数据来源于OSM历史地理数据库,采用Python爬虫批量获取研究范围内的交通基础设施数据;此外,公共自行车站点数据来源于南京市公共自行车有限公司,包含各个公共自行车停放站点的地理位置等信息。
4) 南京市土地利用数据。数据来自于中国基本城市土地利用类型制图(EULUC-China)[29],结合《城市用地分类与规划建设用地标准(GB 50137—2011)》[30],将城市建设用地分为居住用地、工作用地、商业用地和公共及其他用地4类。
2.3 变量选择
本文选择车站客流量为因变量,并从时间尺度和流动方向将其细分为全天客流量、早高峰进站客流量、早高峰出站客流量、晚高峰进站客流量和晚高峰出站客流量5类。
本文从车站属性、连接性和建成环境3个方面选取23个对车站客流特征有潜在影响的自变量,如表 1所示。
表 1 自变量的定义和描述
| 类别 | 变量名称 | 缩写 | 单位 | 变量描述 |
| 车站属性 | 是否为换乘站 | TRANS | — | 1为换乘站,0为其他站 |
| 是否为端点站 | TERM | — | 1为端点站,0为其他站 | |
| 是否毗邻对外交通枢纽 | HUB | — | 1为车站毗邻对外交通枢纽,0为其他情况 | |
| 是否毗邻高校 | COLLEGE | — | 1为车站服务范围内包括高校,0为其他情况 | |
| 运营时长 | OPEN | 月 | 车站开通运营的时长 | |
| 连接性 | 到市中心距离 | DIS_CEN | km | 车站与市中心的直线距离 |
| 道路网密度 | RO_DEN | km/km2 | 车站服务范围内城市道路网密度 | |
| 公交线路密度 | BUS_DEN | km/km2 | 车站服务范围内接驳公交线路密度 | |
| 公交站点数 | BUS_NO | 个 | 车站服务范围内接驳公交站点数 | |
| 停车场数量 | PARKING | 个 | 车站服务范围内的停车场数量 | |
| 公共自行车站点数量 | BICYCLE | 个 | 车站服务范围内公共自行车停放站点数量 | |
| 建成环境 | 人口密度 | POP_DEN | 千人/km2 | 车站服务范围内的常住人口密度 |
| 居住生活类POI密度 | POI_LI | 个/km2 | 车站服务范围内住宿服务和生活服务类设施密度 | |
| 企业办公类POI密度 | POI_OF | 个/km2 | 车站服务范围内公司企业和政府机构类设施密度 | |
| 购物餐饮类POI密度 | POI_SH | 个/km2 | 车站服务范围内餐饮和购物类设施密度 | |
| 文化体育类POI密度 | POI_CU | 个/km2 | 车站服务范围内科教文化和体育休闲类设施密度 | |
| 医疗服务类POI密度 | POI_ME | 个/km2 | 车站服务范围内医疗保健设施密度 | |
| 旅游观光类POI密度 | POI_TR | 个/km2 | 车站服务范围内风景名胜类设施密度 | |
| 居住用地建筑面积比 | LAND_LI | % | 车站服务范围内居住用地的建筑面积占总建筑面积之比 | |
| 工作用地建筑面积比 | LAND_OF | % | 车站服务范围内办公和工业用地的建筑面积占总建筑面积之比 | |
| 商业用地建筑面积比 | LAND_BU | % | 车站服务范围内商业用地的建筑面积占总建筑面积之比 | |
| 公共及其他用地建筑面积比 | LAND_PUB | % | 车站服务范围内公共及其他用地的建筑面积占总建筑面积之比 | |
| 土地利用混合熵 | LAND_MIX | — | 采用熵的概念刻画车站服务范围内土地利用混合程度[6] |
1) 车站属性。
车站属性是指车站的运营功能和区位特征等信息[4-5],本文将是否为换乘站、是否为端点站、是否毗邻对外交通枢纽、是否毗邻高校和开通运营时长作为衡量车站属性的5个变量。其中,是否为换乘站、是否为端点站、是否毗邻对外交通枢纽和是否毗邻高校4个变量为离散变量,开通运营时长为连续变量。
2) 连接性。
轨道交通车站连接性是指乘客到车站的便捷程度或车站到其他区域的交通联系水平[3, 9],本文主要选择车站到市中心的距离、车站服务范围内道路网密度、车站服务范围内公交线路密度、车站服务范围内公交站点数量、车站服务范围内停车场数量和车站服务范围内公共自行车站点数量作为衡量车站连接性的6个变量,这些变量均为连续变量。
3) 建成环境。
建成环境是为了满足人类活动需要而提供的空间背景,是交通发生和吸引的主要影响因素,其核心构成要素包括人口和设施的分布以及土地利用模式[31]。本文主要选取车站服务范围内的人口密度、6类POI设施密度、4类不同用地建筑面积比和土地利用混合熵等12个变量,这些变量均为连续变量。
2.4 指标共线性及空间自相关检验2.4.1 指标共线性
城市轨道交通车站客流特征潜在影响自变量的统计特征及共线性检验结果如表 2所示。
表 2 客流特征潜在影响因素的统计特征
| 类别 | 变量 | 最小值 | 最大值 | VIF |
| 站点自身属性 | TRANS | 0 | 1 | 1.639 |
| TERM | 0 | 1 | 1.278 | |
| HUB | 0 | 1 | 1.373 | |
| COLLEGE | 0 | 1 | 1.770 | |
| OPEN | 8 | 148 | 1.375 | |
| 连接性指标 | DIS_CEN | 0.520 | 43.290 | 2.198 |
| RO_DEN | 0.494 | 15.298 | 2.971 | |
| BUS_DEN | 0 | 11.624 | 1.696 | |
| BUS_NO | 0 | 38 | 2.940 | |
| PARKING | 0 | 188 | 1.879 | |
| BICYCLE | 0 | 19 | 1.973 | |
| 建成环境指标 | POP_DEN | 0.388 | 87.464 | 8.269 |
| POI_LI | 1.951 | 302.439 | 7.248 | |
| POI_OF | 1.005 | 1 685.427 | 7.882 | |
| POI_SH | 0 | 2 661.669 | 4.923 | |
| POI_CU | 0 | 538.310 | 6.612 | |
| POI_ME | 0 | 13.724 | 5.818 | |
| POI_TR | 0 | 122.353 | 2.224 | |
| LAND_LI | 0 | 285.135 | 4.275 | |
| LAND_OF | 0 | 237.508 | 2.885 | |
| LAND_BU | 0 | 273.366 | 3.272 | |
| LAND_PUB | 0 | 126.234 | 2.373 | |
| LAND_MIX | 0 | 0.998 | 1.553 |
由表 2可知:23个自变量的VIF值均小于10,表明本文选取的23个自变量之间不存在严重的多重共线性,具有良好的有效性。
2.4.2 空间自相关性
在空间计量层面,由于自变量属于带地理信息的空间数据,邻近车站之间可能存在空间依赖的现象,因此需要对检验车站间的空间相关性。本文采用Moran′I检验23个自变量在所有车站的空间自相关性,如表 3所示。
表 3 自变量的空间自相关检验结果
| 类别 | 变量 | Moran′I | Z | 显著性 |
| 站点自身属性 | TRANS | 0.016 | 0.814 | 0.415 |
| TERM | 0.036 | 1.472 | 0.141 | |
| HUB | 0.012 | -0.578 | 0.563 | |
| COLLEGE | 0.252 | 8.538 | 0.000 | |
| OPEN | 0.108 | 3.832 | 0.001 | |
| 连接性指标 | DIS_CEN | 0.698 | 23.506 | 0.000 |
| RO_DEN | 0.463 | 15.522 | 0.000 | |
| BUS_DEN | 0.124 | 4.418 | 0.001 | |
| BUS_NO | 0.465 | 15.654 | 0.000 | |
| PARKING | 0.111 | 2.594 | 0.001 | |
| BICYCLE | 0.137 | 0.965 | 0.132 | |
| 建成环境指标 | POP_DEN | 0.958 | 32.431 | 0.000 |
| POI_LI | 0.650 | 21.875 | 0.000 | |
| POI_OF | 0.651 | 22.461 | 0.000 | |
| POI_SH | 0.368 | 12.512 | 0.000 | |
| POI_CU | 0.722 | 24.469 | 0.000 | |
| POI_ME | 0.703 | 23.725 | 0.000 | |
| POI_TR | 0.707 | 24.290 | 0.000 | |
| LAND_LI | 0.271 | 9.211 | 0.000 | |
| LAND_OF | 0.138 | 4.952 | 0.001 | |
| LAND_BU | 0.089 | 3.984 | 0.001 | |
| LAND_PUB | 0.058 | 2.174 | 0.029 | |
| LAND_MIX | 0.165 | 2.426 | 0.001 |
由表 3可知,23个自变量的Moran′I均为正值;除了是否为换乘站、是否为端点站、是否毗邻对外交通枢纽、公共自行车站点数量和公共及其他用地建筑面积比外,其他自变量的Z值均大于1.96且显著性水平均小于0.05,表明整体存在显著的空间自相关,符合建立GWR和MGWR模型的条件。
3 模型结果对比与分析
3.1 模型回归结果分析
选取相同的自变量分别建立OLS、GWR和MGWR客流特征回归模型。在建立GWR和MGWR模型的过程中,首先,采用Gauss函数计算距离权重;其次,以AICc指标作为带宽寻优准则,采用亚利桑那州立大学(Arizona State University)开发的MGWR2.0软件进行求解;最后,采用RSS、Radj2和AICc这3个指标对比分析15个模型回归结果的优劣,如表 4所示。
表 4 15个模型结果的对比分析
| 时间段 | 模型 | RSS | Radj2 | AICc |
| 工作日全天 | OLS | 30.763 | 0.735 | 212.475 |
| GWR | 28.865 | 0.750 | 209.516 | |
| MGWR | 23.778 | 0.774 | 205.722 | |
| 早高峰进站 | OLS | 74.778 | 0.477 | 316.327 |
| GWR | 73.652 | 0.529 | 316.268 | |
| MGWR | 73.296 | 0.574 | 312.102 | |
| 早高峰出站 | OLS | 22.251 | 0.716 | 158.818 |
| GWR | 19.690 | 0.722 | 157.094 | |
| MGWR | 19.376 | 0.730 | 153.856 | |
| 晚高峰进站 | OLS | 19.900 | 0.733 | 149.279 |
| GWR | 15.945 | 0.754 | 140.684 | |
| MGWR | 15.335 | 0.759 | 136.796 | |
| 晚高峰出站 | OLS | 59.427 | 0.496 | 291.750 |
| GWR | 51.448 | 0.577 | 283.466 | |
| MGWR | 49.113 | 0.593 | 280.668 |
由表 4可知:无论是车站的工作日全天客流,还是早高峰进站、早高峰出站、晚高峰进站和晚高峰出站客流量,RSS和AICc从小到到排序为MGWR、GWR、OLS,且Radj从大到小排序为MGWR、GWR、OLS,表明考虑空间自相关的MGWR模型和GWR模型回归结果优于OLS模型;此外,MGWR模型的AICc比GWR的大3.000以上,可以认为MGWR模型在GWR模型的基础上实现了进一步的改进。
3.2 轨道交通车站客流特征分析
本文以南京市128个轨道交通车站为研究对象,采用MGWR模型分别构建工作日全天、早高峰进站、早高峰出站、晚高峰进站和晚高峰出站客流量预测模型,结果表明:全局变量的带宽均为164.360,局部变量的带宽取值范围为[19.660, 35.290]。MGWR模型对所有显著自变量进行标准化处理,各个显著自变量的回归系数如表 5所示。
表 5 MGWR模型回归系数
| 变量 | 工作日全天 | 早高峰进站 | 早高峰出站 | 晚高峰进站 | 晚高峰出站 |
| 常数项 | 0.005 | -0.001 | -0.008 | -0.011 | -0.001 |
| TRANS | 0.281*** | — | 0.234** | 0.232** | 0.222** |
| TERM | 0.103** | 0.208*** | — | — | 0.175*** |
| HUB | 0.220*** | — | 0.100*** | 0.152*** | — |
| OPEN | 0.176*** | 0.233*** | — | 0.097** | 0.226*** |
| DIS_CEN | -0.157* | -0.239** | -0.141*** | -0.184*** | -0.169* |
| BUS_DEN | 0.130** | 0.213*** | — | 0.067* | 0.180** |
| POI_LI | 0.417*** | 0.527*** | — | — | 0.569*** |
| POI_OF | — | -0.401/-0.379/ | 0.485/0.506/ | 0.355*** | -0.331*** |
| POI_SH | -0.123* | — | — | — | — |
| POI_CU | 0.119* | — | — | — | — |
| POI_TR | -0.208/-0.175/ -0.158***a | -0.359/-0.244/ | — | — | -0.321/-0.216/ |
| LAND_OF | — | — | 0.123** | 0.084* | — |
| LAND_BU | 0.303*** | — | 0.193*** | -0.299/0.341/ | 0.270*** |
| LAND_PUB | — | — | 0.056** | 0.080** | — |
| LAND_MIX | -0.087* | -0.159** | — | — | -0.168** |
| 注:1) *表示在90%置信区间上显著,**表示在95%置信区间上显著,***表示在99%置信区间上显著;2) a表示该变量为局部变量,其回归系数用“最小值/中位数/最大值”形式表示。 | |||||
由表 5可知:
1) 不同模型的显著自变量存在差异。工作日全天客流预测模型有12个显著自变量,其中全部变量11个、局部变量1个;其他4个客流预测模型的显著自变量为7~10个,除早高峰进站客流量预测模型有2个局部变量外,其他3个客流预测模型也只有1个局部变量。
2) 只有“到市中心距离”这个自变量在所有客流预测模型中都是显著的,且回归系数为负值,表明距离市中心越近的车站的客流量集聚性越明显。
3) 早高峰进站和晚高峰出站客流预测模型中的显著自变量具有相似特征,例如居住生活类POI密度对这2个模型都有显著的正影响,表明周边居住、生活类设施占比较高的车站对早高峰进站和晚高峰出站客流有很强的吸引作用。同理,早高峰出站和晚高峰进站客流预测模型中的显著自变量也具有相似特征,例如企业办公类POI密度、工作用地建筑面积比、商业用地建筑面积比和公共及其他用地建筑面积比3个自变量对这2个模型都有显著的正影响,表明周边居住、生活类设施占比不高的车站对早高峰出站和晚高峰进站客流有很强的吸引作用。
4) 同一局部变量影响的模型数量不同。例如,旅游观光类POI密度是工作日全天、早高峰进站和晚高峰出站3个客流量预测模型的局部变量;企业办公类POI密度是早高峰进站和早高峰出站2个客流量预测模型的局部变量;商业用地建筑面积比仅是晚高峰进站客流量预测模型的局部变量。
3.3 局部变量对车站客流的空间作用分析
为进一步探讨局部变量对不同车站客流量的影响程度,采用ArcMap10.2软件将表 5中的5个模型中的6个局部变量对不同车站客流量的影响进行空间分析,如图 2所示。
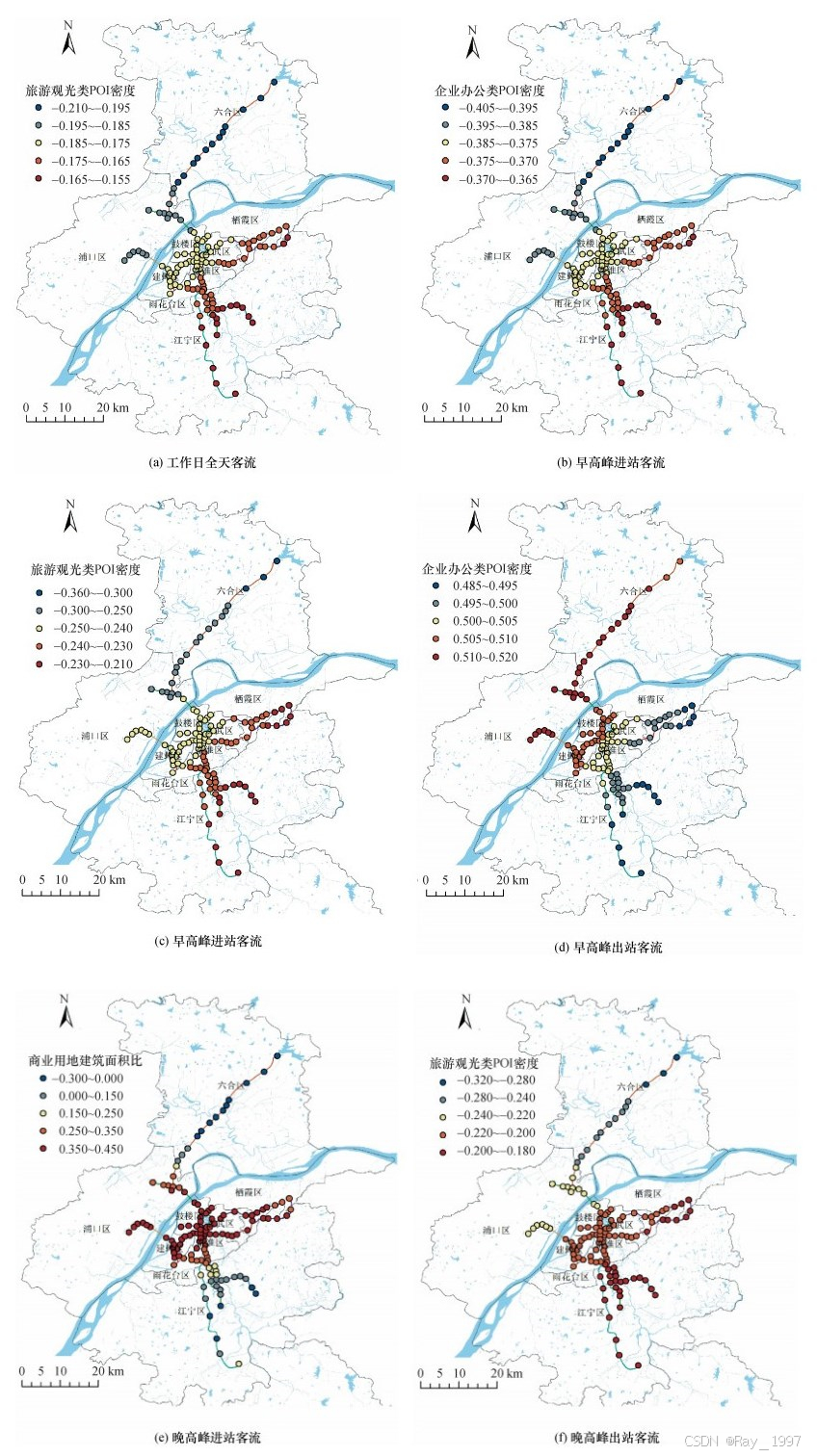 |
| 图 2 局部变量回归系数的空间分布 |
由图 2可知,局部变量对城市轨道交通车站客流量的影响程度在空间分布上既不是统一的,也不是随机的,而是呈现出一定的规律性,具体特征如下:
1) 旅游观光类POI密度对工作日全天客流量有负向影响,回归系数的范围为[-0.208, -0.158],且取值越小说明对客流的影响程度越大,如图 2a所示。主要原因可能是以旅游观光为目的的乘客出行活动主要集中在节假日,因此旅游观光类POI分布较为集中的车站工作日客流量的负向影响程度较大。例如,S8宁天线位于六合区内的金牛湖、八百桥和沈桥车站周边分布较多的旅游区与度假村,回归系数均低于-0.200,对客流量的影响程度最大;而位于江宁区内的车站,回归系数均高于-0.170,对客流量的影响程度最小。
2) 企业办公类POI密度对早高峰进站客流量有负向影响,回归系数的范围为[-0.401, -0.363],如图 2b所示。这主要是因为早高峰进站客流以通勤客流为主,他们大多数都是从居住地出发前往就业地的通勤乘客;回归系数的总体空间分布呈南高北低的趋势,对六合区内的车站影响程度大,而对江宁区的车站影响程度小。
3) 旅游观光类POI密度对早高峰进站客流量也有负向影响,回归系数的范围为[-0.359, -0.214],如图 2c所示。回归系数的空间分布呈东南高、西北低的趋势,同样对六合区内的金牛湖、八百桥和沈桥车站早高峰进站客流量的影响程度最大。
4) 企业办公类POI密度对早高峰出站客流有正向影响,回归系数的范围为[-0.486, -0.519],如图 2d所示。这主要是与早高峰通勤客流的流向有关;同时,回归系数的空间分布呈现西北高、东南低的分布趋势。其中,位于长江以北的浦口区和六合区的林场、文德路和雨山路等车站的回归系数最高,且基本都在0.510以上,说明提高企业办公类POI的密度对该区域内车站早高峰出站客流量的促进影响最为显著;而位于江宁区和栖霞区的禄口机场、中国药科大学和仙林湖等车站的回归系数均低于0.495,该区域内企业办公类POI密度对车站客流量的影响能力相对较弱。
5) 商业用地建筑面积比对晚高峰进站客流量的影响在空间上存在相当大的差异,研究区域内回归系数的范围为[-0.299, -0.382],如图 2e所示。总体来看,该指标对大部分车站的晚高峰进站客流有正向影响,其参数值以城市中心区为中心向外逐渐降低。例如,城市中心区内的上海路、三山街和鼓楼等车站位于新街口、夫子庙和湖南路等大型商圈附近,对晚高峰进站客流具有很强的吸引作用,回归系数均在0.350以上;而六合区东部和江宁区南部的方州广场、雄州和翔宇路北,指标的回归系数均为负值,表明这3个车站服务范围内的商业用地建筑面积比的增加不会产生更多客流量,主要原因是这3个车站远离市中心且车站周边居住人口较少。
6) 旅游观光类POI密度对晚高峰出站客流量有负向影响,回归系数的范围为[-0.321, -0.188],如图 2f所示。回归系数取值的空间分布呈东南高、西北低的趋势,这与早高峰进站客流量的变化趋势是一致。
4 结论
本文考虑进出站客流的潮汐特性,结合不同时间尺度将车站客流量细分为全天客流量、早高峰进站客流量、早高峰出站客流量、晚高峰进站客流量和晚高峰出站客流量5类,采用MGWR模型构建车站客流特征分析模型,从微观层面刻画车站客流量与影响因素的相互依赖关系,对南京市轨道交通系统进行实例分析。相比OLS和GWR模型,MGWR模型的结果更可靠,这主要是因为MGWR模型能够捕捉到不同变量的不同影响尺度,避免了太多噪声导致的结果偏差。不同模型的显著自变量存在差异,忽略早晚高峰客流影响的全天客流量预测模型拥有的显著自变量最多;影响早高峰进站和晚高峰出站、早高峰出站和晚高峰进站客流量预测模型的显著自变量具有相同的变化特征;影响早高峰进站和早高峰出站、晚高峰进站和晚高峰进站客流量预测模型的显著自变量具有相反的变化特征。
由于数据获取的难度,本文对自变量的细化还有待进一步深化;并且没有对比分析不同类型车站的进站和出站客流量、工作日和节假日客流量的影响差异,这些都是后续研究的重点。
























 1075
1075

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








