弹性力学变分原理：最小势能原理

对于一般的力学问题，有两种思路，一种是从局部出发，研究每一个质点或者微元的状态。一种是从整体出发，研究物体整体的性质。前者很自然的将问题抽象得到了微分方程，后者往往对应一个最小作用量原理，如弹性问题的最小势能原理。

最小势能原理是结构力学中的一个基本原理。它表明，对于一个在外力作用下的弹性体，平衡状态下的势能是所有可能的位移场中的最小值。为了推导出最小势能原理，我们可以从虚功原理出发，通过变分法来证明。

总势能定义

在弹性体中，总势能 $\Pi$ 包括应变能和外力势能。其表达式为：

$\Pi =U-W$

其中：

• $U$ 是系统的应变能。
• $W$ 是外力做的功。
  

应变能和外力做功的表达式

应变能 $U$ 可以表示为：

$U=\frac{1}{2}{\int }_{\Omega }\sigma :ϵd\Omega$

其中，$\sigma$ 是应力张量，$ϵ$ 是应变张量。

外力做功 $W$ 可以表示为：

$W={\int }_{\Omega }b\cdot ud\Omega +{\int }_{\partial {\Omega }_t}t\cdot udS$

其中，$b$ 是体力，$u$ 是位移，$t$ 是表面力。

总势能的变分

考虑总势能 $\Pi$ 的变分 $\delta \Pi$：

$\delta \Pi =\delta U-\delta W$

其中：

$\delta U=\frac{1}{2}{\int }_{\Omega }(\sigma :\delta ϵ+\delta \sigma :ϵ)d\Omega$

将 $\sigma =C:ϵ$ 带入上式：

$\delta U=\frac{1}{2}{\int }_{\Omega }(C:ϵ:\delta ϵ+C:\delta ϵ:ϵ)d\Omega ={\int }_{\Omega }C:ϵ:\delta ϵd\Omega ={\int }_{\Omega }\sigma :\delta ϵd\Omega$

$\delta W={\int }_{\Omega }b\cdot \delta ud\Omega +{\int }_{\partial {\Omega }_t}t\cdot \delta udS$

将应变能和外力做功的变分代入总势能的变分中：

$\delta \Pi ={\int }_{\Omega }\sigma :\delta ϵd\Omega -\left({\int }_{\Omega }b\cdot \delta ud\Omega +{\int }_{\partial {\Omega }_t}t\cdot \delta udS\right)$

利用虚功原理

根据虚功原理，对于任意虚位移场 $\delta u$ ，有：

${\int }_{\Omega }\sigma :\delta ϵd\Omega ={\int }_{\Omega }b\cdot \delta ud\Omega +{\int }_{\partial {\Omega }_t}t\cdot \delta udS$

我们得到：

$\delta \Pi =0$

这表明，在平衡状态下，总势能 $\Pi$ 的一阶变分为零。这意味着，总势能在平衡状态下取极值。

最小势能原理

注意，上面的步骤推导出总势能的一阶变分为零，只能说明势能取极值，而无法说明势能取极小值。不过，我们可以从能量的角度想一下，如果平衡状态的能量取极大值，而非平衡状态的能量更小，那这个世界感觉要乱套了。数学上的证明需要能量的二阶变分是否大于零。

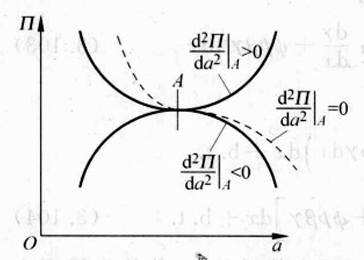
势能的二阶变分推导

计算总势能的二阶变分 ${\delta }^2\Pi$：

${\delta }^2\Pi =\delta (\delta \Pi )$

我们需要对 $\delta \Pi$ 再进行一次变分。首先计算 应变能的二阶变分 ${\delta }^{2}U$ 为：

${\delta }^{2}U=\delta \left({\int }_{\Omega }\sigma :\delta ϵd\Omega \right)$

由于应力 $\sigma$ 是应变 $ϵ$ 的函数，并且 $\sigma =C:ϵ$，其中 $C$ 是弹性刚度张量，$ϵ=\nabla u$ 是位移的函数，所以 $\delta \sigma =C:\delta ϵ$。因此：

${\delta }^{2}U={\int }_{\Omega }\delta \sigma :\delta ϵd\Omega$

代入 $\delta \sigma =C:\delta ϵ$，我们得到：

${\delta }^{2}U={\int }_{\Omega }(C:\delta ϵ):\delta ϵd\Omega$

外力做功的二阶变分 ${\delta }^{2}W$ 为：

${\delta }^{2}W=\delta \left({\int }_{\Omega }b\cdot \delta ud\Omega +{\int }_{\partial {\Omega }_t}t\cdot \delta udS\right)$

由于 $b$ 和 $t$ 是常量，它们的变分为零，因此：

${\delta }^{2}W={\int }_{\Omega }b\cdot \delta (\delta u)d\Omega +{\int }_{\partial {\Omega }_t}t\cdot \delta (\delta u)dS$

实际上，由于 $\delta (\delta u)$ 为零，所以 ${\delta }^{2}W=0$。

结合 ${\delta }^{2}U$ 和 ${\delta }^{2}W$，我们得到总势能的二阶变分 ${\delta }^2\Pi$ 为：

${\delta }^2\Pi ={\delta }^{2}U-{\delta }^{2}W={\int }_{\Omega }(C:\delta ϵ):\delta ϵd\Omega =2{\int }_{\Omega }U(\delta ϵ)d\Omega$

可得，应变能二阶变分等于应变变分产生的应变能，由于应变能是正定的，所以。

总结

最小势能原理说明，在弹性体的平衡状态下，系统的总势能达到极小值。这一结论为结构分析和有限元方法提供了理论基础，通过变分法，我们能够求解平衡状态下的位移场和应力场。由于本文使用了线弹性本构方程，所以上面推导适用范围为线弹性体，但是关于最小势能原理还有更多的值得探讨的主题：

• 如何通过最小势能原理求解平衡方程？
• 最小势能原理的适用范围是什么？ 对于非线弹性体是否能够推广？