1 为什么要学数学?
光学知识体系复杂多样,宏观微观抽象交杂,光是电磁波,而电磁波的本质是波,波的本质是三角函数。因此,想要学好光学必须学好数学基础,三角函数及其背后的物理意义,虽然三角函数是光学中基础的基础,但在理论计算中计算不方便,常使用复变函数中的欧拉公式。因而,三角函数、矢量计算、复变函数基础等三大部分数学基础是入门光学的必备数学知识基础。
2 三角函数
单纯从数学的角度上来看,三角函数
f
(
x
)
=
A
c
o
s
(
ω
x
+
φ
)
f(x)=Acos(\omega x+\varphi)
f(x)=Acos(ωx+φ) 从本质上来说三角函数是角度的函数,即自变量
x
x
x 是一个角度,
(
ω
x
+
φ
)
(\omega x+\varphi)
(ωx+φ)是一个角度,
φ
\varphi
φ 也是一个角度,而
A
A
A 是决定振动的大小,也即下图中左边圆的半径。
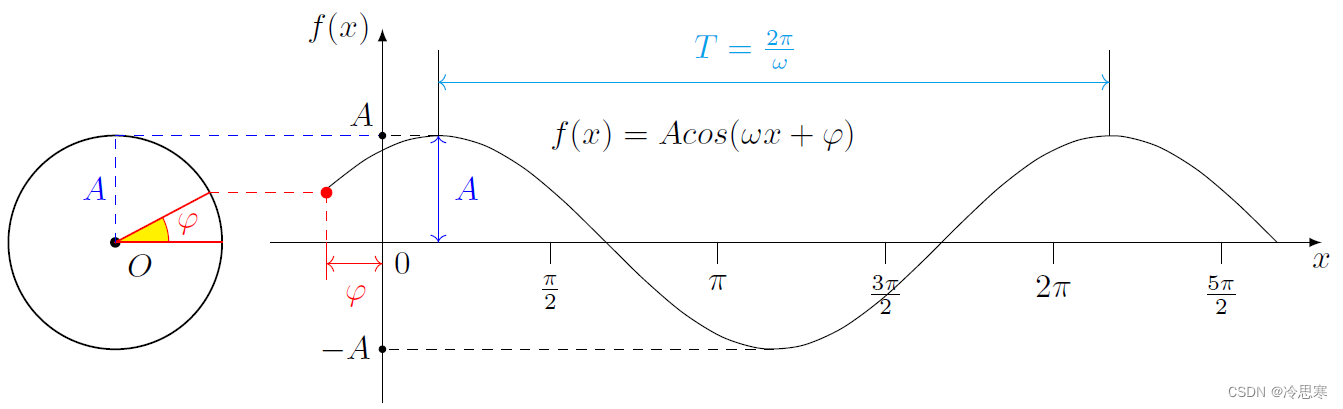
从物理的角度上来看,三角函数是简谐波,因此,三角函数的各个参数在物理上做如下定义:
- A A A :振幅,表示振动幅度的最大值;
- ω x + φ \omega x+\varphi ωx+φ :相位,表示 x x x 所处位置的角度大小;
- φ \varphi φ :初相位:表示 x = 0 x=0 x=0 时的角度大小,即还没开始运动时的初始角度;
- ω \omega ω:角速度,表示旋转一周的速度。
在光学中最常见的波函数是: f ( x ) = A c o s ( ω t + k ⃗ x + φ ) f(x)=Acos(\omega t +\vec{k}x+\varphi) f(x)=Acos(ωt+kx+φ),该波函数中包含了时间 t t t 和空间 x x x 两个纬度的变量,在研究光波时,常将一个变量固定而研究另一个变量的波函数。其中: k ⃗ \vec{k} k 是波矢,表示光波前进的方向,在数值上 k = 2 π λ k=\frac{2\pi}{\lambda} k=λ2π。
3 矢量计算
标量和矢量都可以表示数量的大小,但标量仅仅是一个数值,只能表示大小,而矢量(向量)既可以表示大小,同时也可以表示方向。因此,标量只表示一个数值大小,方向是任意的,而矢量不仅表示大小,同时也确定了其所指的方向。矢量在一定程度上更方便计算和分析,比如力的分解与合成、光的分解与合成。掌握矢量的本质有利于学习偏振性、晶体光学等知识。
在数学上,常用一条有方向的线段来表示矢量(向量),线段长度表示矢量的大小,叫做向量的模,线段方向表示矢量的方向。如下图所示,以
A
A
A 为起点、
B
B
B 为终点的有向线段所表示的向量记作:
A
B
⃗
\vec{AB}
AB,也可用带箭头的字母表示:
a
⃗
\vec{a}
a。在数学上只研究与起点无关的向量,称为自由向量,简称向量。
矢量计算基础过于既简单这里不作详细介绍,学者自行查阅相关的数学书籍。
4 复数基础
4.1 复数概念
- z = x + y i z=x+yi z=x+yi 称为复数,其中 x x x 称为实部,是一个实数,与实数无本质区别, y i yi yi 是虚部, i i i 是虚数因子,定义为: i 2 = − 1 i^2=-1 i2=−1;
- z ˉ = x − y i \bar{z}=x-yi zˉ=x−yi 称为复数 z z z 的共轭复数;
- 复数的模 ∣ z ∣ |z| ∣z∣:实部与虚部的平方和的正的平方根的值, ∣ z ∣ = x 2 + y 2 |z|=\sqrt{x^2+y^2} ∣z∣=x2+y2;
- 辐角 A r g ( z ) Arg(z) Arg(z):在复平面中实轴与复数向量的夹角,其中在 [ − π , π ] [-\pi,\pi] [−π,π]范围内的辐角称为主辐角 a r g ( z ) arg(z) arg(z)。
4.2 复数的三种表达形式
- 一般式: z = x + y i z=x+yi z=x+yi
- 指数式: z = r e i θ z=re^{i\theta} z=reiθ
- 三角函数式: z = r ( c o s θ + i s i n θ ) z=r(cos\theta+isin\theta) z=r(cosθ+isinθ)
其中:
- 模: ∣ z ∣ = r |z|=r ∣z∣=r
- 辐角: A r g ( z ) = θ Arg(z)=\theta Arg(z)=θ
由此有如下结论:
- x = r c o s θ x=rcos\theta x=rcosθ
- y = r s i n θ y=rsin\theta y=rsinθ
- z = r e i θ = r ( c o s θ + i s i n θ ) z=re^{i\theta}=r(cos\theta+isin\theta) z=reiθ=r(cosθ+isinθ)
- e i θ = c o s θ + i s i n θ e^{i\theta}=cos\theta+isin\theta eiθ=cosθ+isinθ(欧拉公式)
4.3 复数计算
设有两个复数: z 1 = a + b i z_1=a+bi z1=a+bi、 z 2 = c + d i z_2=c+di z2=c+di,则有如下运算法则:
- 加法: z = z 1 + z 2 = ( a + c ) + ( b + d ) i z=z_1+z_2=(a+c)+(b+d)i z=z1+z2=(a+c)+(b+d)i
- 减法: z = z 1 − z 2 = ( a − c ) + ( b − d ) i z=z_1-z_2=(a-c)+(b-d)i z=z1−z2=(a−c)+(b−d)i
- 乘法: z = z 1 × z 2 = a c + a d i + c b i + b d i 2 = ( a c − b d ) + ( a d + b c ) i z=z_1 \times z_2=ac+adi+cbi+bdi^2=(ac-bd)+(ad+bc)i z=z1×z2=ac+adi+cbi+bdi2=(ac−bd)+(ad+bc)i
- 除法: z = z 1 z 2 = a + b i c + d i = ( a + b i ) ( c − d i ) ( c + d i ) ( c − d i ) = a c − a d i + b c i − b d i 2 c 2 + d 2 = ( a c + b d ) + ( b c − a d ) i c 2 + d 2 = a c + b d c 2 + d 2 + b c − a d c 2 + d 2 i z=\frac{z_1}{z_2}=\frac{a+bi}{c+di}=\frac{(a+bi)(c-di)}{(c+di)(c-di)}=\frac{ac-adi+bci-bdi^2}{c^2+d^2}=\frac{(ac+bd)+(bc-ad)i}{c^2+d^2}=\frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i z=z2z1=c+dia+bi=(c+di)(c−di)(a+bi)(c−di)=c2+d2ac−adi+bci−bdi2=c2+d2(ac+bd)+(bc−ad)i=c2+d2ac+bd+c2+d2bc−adi
乘法与除法使用辐角和模长的计算方法:
- 乘法:辐角相加,模长相乘
- 除法:辐角相减,模长相除
4.3 复平面
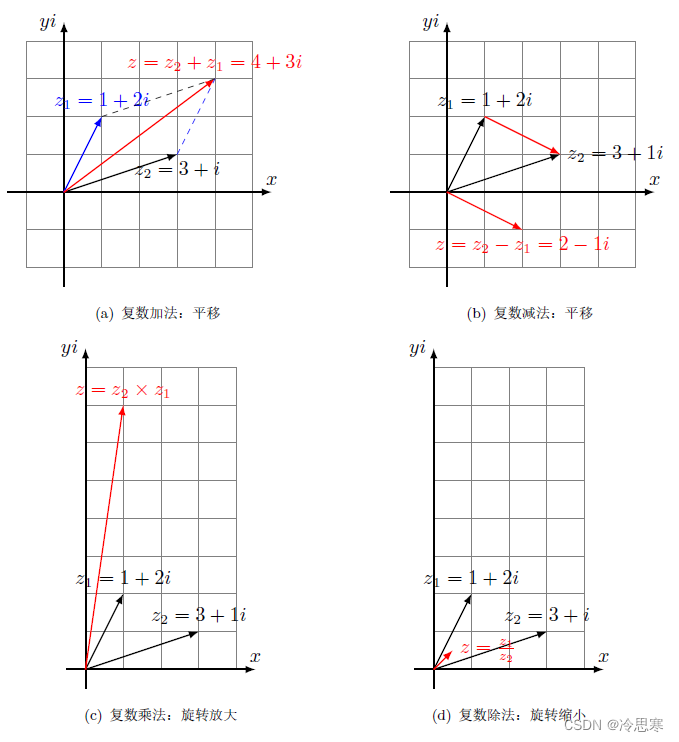
如下图所示以实部为实轴,虚部为虚轴的直角坐标称为复平面,下面四幅图分别给出了复数的四则运算法则的几何意义:
- 加法:【平移】四边形法则
- 减法:【平移】三角形法则
- 乘法:
- 旋转:辐角相加
- 放大:模长相乘
- 除法:
- 旋转:辐角相减
- 缩小:模长相除
5 欧拉公式
结合复数的指数表示法:
z
=
r
e
i
θ
z=re^{i\theta}
z=reiθ 和指数表示法:
z
=
r
(
c
o
s
θ
+
i
s
i
n
θ
)
z=r(cos\theta+isin\theta)
z=r(cosθ+isinθ),两边同时除以模
r
r
r 后得欧拉公式:
e
i
θ
=
c
o
s
θ
+
i
s
i
n
θ
e^{i \theta}=cos\theta+isin\theta
eiθ=cosθ+isinθ。
光是电磁波,电磁波的波函数是余弦函数,因此,常用复数的实部表示光波函数。既然有三角函数可以表示波函数,那为什么还非得要用复数来表示波函数呢?
这得益于复数具有矢量的性质,在运算方面更优异于三角函数,这在光强、光的合成等光学理论计算中有重要应用。
愿各位读者学有所获,由于编者水平有限,文中难免存在一些缺点和错误,殷切期望读者批评指正。






















 7925
7925











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








