Logistic回归原理浅谈

最新推荐文章于 2021-06-26 10:01:50 发布
最新推荐文章于 2021-06-26 10:01:50 发布
阅读量2.4k 收藏 4
点赞数
分类专栏： 机器学习
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/lfdanding/article/details/50719097
版权

原文参考http://blog.csdn.net/ariessurfer/article/details/41310525
Logistic回归为概率型非线性回归模型，是研究二分类观察结果与一些影响因素之间关系的一种多变量分析方法。通常的问题是，研究某些因素条件下某个结果是否发生，比如医学中根据病人的一些症状来判断它是否患有某种病。
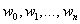
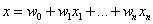
在讲解Logistic回归理论之前，我们先从LR分类器说起。LR分类器，即Logistic Regression Classifier。在分类情形下，经过学习后的LR分类器是一组权值这里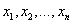写图片描述，当测试样本的数据输入时，这组权值与测试数据按照线性加和得到
这里写图片描述
这里这里写图片描述是每个样本的n个特征。
解出x之后，按照sigmoid函数的形式求出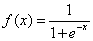这里写图片描述
sigmoid函数的图像如图所示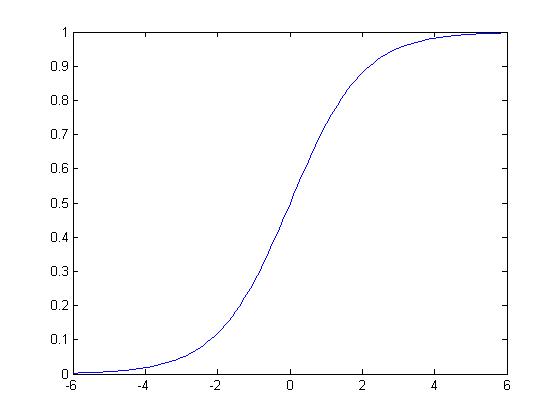这里写图片描述
sigmoid函数的定义域为

最低0.47元/天 解锁文章
lfdanding
关注
专栏目录
机器学习之逻辑回归原理
SKIp121whats112的博客
01-28 1559
机器学习之逻辑回归原理
逻辑回归原理（英文）
05-24
二分类问题是指预测的y值只有两个取值（0或1），二分类问题可以扩展到多分类问题。例如：我们要做一个垃圾邮件过滤系统，是邮件的特征，预测的y值就是邮件的类别，是垃圾邮件还是正常邮件。对于类别我们通常称为正类（positive class）和负类（negative class），垃圾邮件的例子中，正类就是正常邮件，负类就是垃圾邮件。
Logistic回归简介
两只橙的博客
09-22 888
1、线性回归的主要思想就是通过历史数据拟合出一条直线，用这条直线对新的数据进行预测。（例如：位于线性函数两边的分别为A.B类）2、现实世界中的影响因素很多，因此我们需要使用多元线性函数来描述一个事件（结果）3、多元线性函数：研究二分类观察结果y与一些影响因素（x1,x2,x3,…,xn）之间关系的一种多变量分析方法，例如医学中根据病人的一些症状来判断它是 否患有某种病。4、多元线性回归公式： 5
十一.Logistic回归原理
weixin_36128607的博客
06-26 459
目录1.回归和分类2.Logistic函数3.Logistic回归模型4.损失函数(1)交叉熵(2)极大似然估计 1.回归和分类 回归的预测值yyy为连续值，分类的预测值yyy为离散值。 Logistic回归的名字中虽然有回归二字，但其实是二分类算法。 2.Logistic函数 Logistic函数为两端饱和S型曲线函数，它将自变量的输出值固定在[0,1][0,1][0,1]区间上。 Logistic函数原型为： g(z)=11+e−z g(z)=\frac{1}{1+e^{-z} } g(z)=1+e−
Logistic回归的基本原理(简单介绍)
qq_38023849的博客
12-18 4633
目录 LR回归 概率解释   Logistic 回归是一种分类器，功能与贝叶斯分类器，SVM等分类器一致，是用于分类的，而不是进行数据回归的。下面简单介绍下整个LR模型的基本原理，主要有两个核心问题，1是LR如何分类，2是如何得到模型内相应的参数。 LR回归   首先介绍sigmoid函数，sigmoid函数可以把任意实数域内的元素映射到(0，1)(0，1)(0，1)之间。表达式如下： y(x)=11+e−x(1)y(x)=\frac{1}{1+e^{-x}}\tag{1}y(x)=1+e−x1​(1)
逻辑回归原理
weixin_34288121的博客
03-10 114
来自：刘建平 逻辑回归是分类算法，可以处理二元分类和多元分类。 名字里有“回归”二字，但不是回归算法。为什么名字有“回归”这个误导词？因为它的原理有回归模型的影子。 1. 从线性回归到逻辑回归 线性回归模型是求Y和X之间的线性关系系数Θ，满足Y= XΘ。此时Y是连续的，所以是回归模型。 想要Y是离散的话，对Y再做一次函数转换，变为g(Y)。如果g(Y)结果类别是两种，就是二元...
泛统计理论初探——浅谈回归问题
喷火龙与水箭龟的博客
09-13 743
数据挖掘-回归问题探讨 浅谈连续回归和离散回归 众所周知，回归问题可以根据因变量的离散或连续分为连续回归（线性回归、非线性回归）与分类回归。其中，为了解决分类回归问题，在经典的回归假设基础上，引入了对数几率的概念，将数值转化为概率，并通过设定阈值最终确定因变量的类型。 传统的回归方法是研究因变量是连续的问题，比如研究影响身高的因素，身高是一个相对连续的量，因此该类问题是通过线性回归可以进行研究的。...
浅谈逻辑回归、BP传播、数据正归一化
cottpaddedC的博客
12-14 757
看了这篇文章你能学到什么： 逻辑回归，神经网络学习的基础 神经网络节点权重的计算方法 BP反向传播如何计算损失函数和代价函数 写这篇文章的目的： 当然，最初写这一篇文章的初心当然不是写一些密密麻麻的公式，并解释其中的原理，在网上看了很多的博客，基本上都是一直在解释算法是怎么实现啊，巴拉巴拉一大堆。对于我这种初学者来说那个公式看到头疼。后面我想了一下，算法的本身难道最后不就是编程来实现的吗，那如果我们用代码来反推公式，是不是会更加容易去理解公式呢？ 浅谈逻辑回归 我们学习这个东西就从三个方面入手，是什么，能做
浅谈特征选择的原理和Python实现
WEILING123的博客
04-27 809
0.引言 在现实世界中，我们总是倾向于收集尽可能多的特征来对一个事物进行描述，以期能够全面准确的刻画事物。然而，我们了解事物的目的是时刻变化着的，所以并非每一次对事物的刻画都需要所有特征。例如在机器学习领域众所周知的西瓜，描述西瓜的特征有很多，包括：大小、色泽、敲声、纹理、触感、根蒂等。了解西瓜的目的（学习任务）也各不相同：好吃、好闻、好看等。显然，若学习任务是判断一个西瓜是否好看，则只需要大小、色泽、纹理等特征即可，这些特征即是“相关特征”。若需求为判断西瓜是否好吃，只需要根蒂、敲声即可，其他的特征则为“
逻辑回归（Logistic Regression）原理
记忆碎片的博客
05-02 939
文章目录sigmoid函数逻辑回归原理推导极大似然估计法与梯度下降法估计模型参数极大似然估计梯度下降法 sigmoid函数 sigmoid函数公式: σ(x)=11+e−x \sigma(x)=\frac{1}{1+e^{-x}} σ(x)=1+e−x1​ 当x趋近于负无穷时，函数值趋近于0；当x趋近于正无穷时，y趋近于1；当x= 0时，y=0.5。这种特征使得sigmoid函数很适合用来做二...
[原理篇] 逻辑回归
沈春旭的博客
10-14 1225
1. Logistic Regression基本模型     Logistic Regression 模型是广义线性模型中的一种，属于线性分类模型。对于类似上图的分类问题，需要找到一条直线，将两个不同的类区分开。多维情况下，可以利用如下线性函数描述该超平面。 W为权重，b为偏置。多维情况下，两者都是向量。实际应用中，通过对训练样本的学习确定该超平面。其中，我们可以使用阈值函数将样本映...
logistic回归原理
最新发布
09-10
逻辑回归的原理是由线性回归模型演变而来的，因此含有“回归”二字，但它并不是一个回归算法，而是属于广义线性模型的一类。[2] 逻辑回归的基本原理可以概括为以下几个步骤： 1. 寻找预测函数：逻辑回归模型通过定义...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值