目录
运动的描述
两类运动学知识点
1.位置矢量
2.运动方程
3.轨道方程
4.位移
5.速度
(1)平均速度
(2)瞬时速度(简称速度)
(3)速率
平均速率:
瞬时速率:
6.加速度
(1)平均加速度
(2)瞬时加速度(简称加速度)
题1
题目描述
已知质点沿x轴作直线运动,其运动方程为,式中x的单位为m,t的单位为s.求:(1)质点在运动开始后4.0s内的位移的大小;(2)质点在该时间内所通过的路程;(3)t = 4s时质点的速度和加速度.
题解
第一问求位移大小,位移通过位置矢量来求 ,因为是沿x轴,所以只是一个一维的问题,比较简单。位置矢量差反映的就是从初位置到末位置的位置变化。
已知:
故而运动方程写成:
在4.0s内,位移:
注意题目是求位移的大小,所以最终:
第二问求路程,路程就需要通过运动方程来求了。运动方程我们在第一问已经求出来了,路程是可以有很多种情况的,于是我们要通过速度为0的时刻质点所在位置来判断它的路程到底是哪个。通过运动方程求出速度,令速度为0,得到了两个时刻,进而知道了质点的位置变化是这样的:
最后求出路程即可。
先求出速度:
令速度为0:
解得:
通过运动方程求得2s时的位置:
最后就可以求得路程:
第三问求某一时刻的速度和加速度,根据第二问很容易就可以求得速度的大小和方向,是沿x轴的负方向的;加速度就要速度对时间求一阶导,再代入数值即可。
在质点运动中,通常有两类问题,第一类是已知运动方程,求速度,加速度;第二类是已知加速度,求速度,运动方程。
即:
题2(第一类问题)
题目描述
质点的运动方程为和
,式中x,y的单位为m,t的单位为s.试求:(1)初速度的大小和方向;(2)加速度的大小和方向.
关于运动方程
运动方程可以写成这个形式,

对应题目中的和
题解
第一问求初速度的大小和方向,直接求导代入0即可,得到矢量式,既包含大小,也包含方向。符合题目要求。
第二问同理
题3(第二类问题)
题目描述
一气球以匀速率从地面上升,由于风的影响,它获得了一个水平速度
(b为常量,y为上升高度),以气球出发点为坐标系原点,向上为y轴正向,水平沿风向为x轴正向.求:(1)气球的运动方程;(2)气球的轨迹方程.
题解
第一问求的是运动方程,我们现在已知速度,可以直接通过速度来求得运动方程,注意积分过程中变量的转换就可以可以顺利求出来,具体过程如下:
先把y轴和x轴方向上的速度表示出来:
故而总体的速度表示为:
根据速度公式,可以得到运动方程:
转化成求标量的形式:
那么接下来的目标就是求x和y对于时间t的函数了:
由题目已知的关系:
首先对y整理一下:,两边同时积分:
,解得
.
再对x整理:,这样无法积分,所以根据
可以将它转化成:
,这个时候就可以两边同时积分啦:
,解得
.
最终,运动方程为:
第二问求轨迹方程,在这道题中,只有x和y轴,把二者的函数关系写出来、把时间t约掉即可。
,把t代进去,就可以约掉t了:
整理得到最终的轨迹方程为:
,应该为一条抛物线。
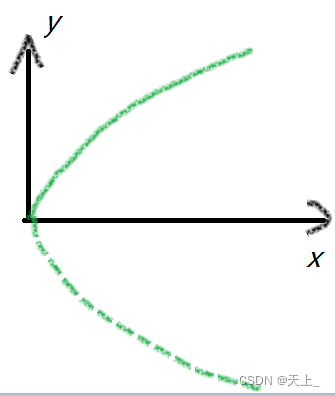
题4
题目描述
一质点沿x轴运动,其加速度a与位置坐标x的关系为,如果质点在原点处的速度为零,试求其在任意位置处的速度。(SI)为国际单位制
题解
将式子整理一下:,两边同时积分:
.
解得:,因为其在原点处的速度为0,且初始加速度大于0,所以速度一定是大于0的,故而可以得到:
圆周运动知识点
1.曲率
两条切线间的夹角为
,两点间的弧长为
2.曲率半径
3.角速度、角加速度
4.线量和角量的关系
推导出
5.平面曲线运动
切向
法向
题5
题目描述
一飞轮以速率转动,受到制动而做匀减速运动,经
后静止.求:(1)求角加速度
和从制动开始到静止飞轮的转数N;(2)求制动开始后
时飞轮的角速度
;(3)设飞轮的半径
,求
时飞轮边缘上任一点M的速度和加速度.
题解
第一问,初角速度
时
,代入
求得
从开始制动到静止飞轮的角位移及转数分别为:
第二问,时飞轮的角速度为:
第三问,时飞轮边缘上M点的速度为:
相应的切向加速度和向心加速度为:
相对运动知识点
速度变换定理:
绝对速度:
相对速度:
牵连速度:
加速度变换也是类似的
当两个坐标之间的相对速度(牵连速度)不是常量时,就有一个牵连加速度
则绝对加速度=相对加速度+牵连加速度,即
题6
题目描述
一电梯以的加速度下降,其中一乘客在电梯开始下降后0.5s时用手在离电梯底板1.5m高处释放一小球.求:(1)小球落到底板上所需的时间;(2)它对地面下落的距离.
题解
第一问,以电梯为参照,小球的初速度
设球相对于地的加速度为,即绝对加速度;球相对于电梯的加速度为
,即相对加速度;电梯相对于地的加速度为
,即牵连加速度。
故而有:(取竖直向下为正方向)
现在要求小球落到底板上所需的时间,所以显然需要知道小球相对于电梯的加速度,这里设为,时间设为
,
为小球初始位置到电梯底板的高度1.5m,
代入数据可求得
第二问,相对于地来说,小球的初速度应该用电梯对地的加速度来进行计算,即
所以相对于地面下落的距离就可以求了:
题7
题目描述
一个人骑车以的速率自东向西行进时,看见雨点垂直下落,当他的速率增至
时看见雨点与他前进的方向成120度角下落,求雨点对地的速度。
题解
设雨点相对于地面的速度为,雨点相对于人的速度为
,人相对于地面的速度为
.
由速度变换定理,有:
第一种情况,

第二种情况,
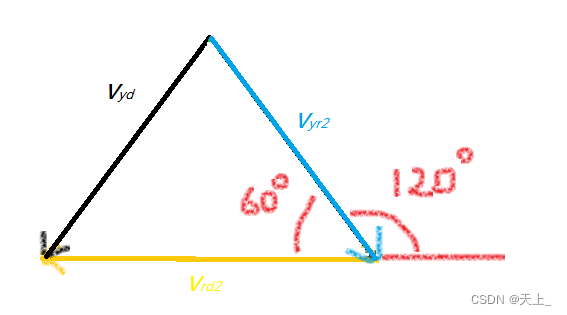
由几何关系可知,
最后也又几何关系:
得:
即最终雨点对地的速度为36km/h。
end








 文章详细阐述了物理中的运动学概念,包括位置矢量、运动方程、加速度的计算,以及圆周运动和相对运动的相关知识。通过多个例题解析了如何根据运动方程求解速度、加速度和轨迹方程,展示了从运动方程到实际物理现象的推导过程。
文章详细阐述了物理中的运动学概念,包括位置矢量、运动方程、加速度的计算,以及圆周运动和相对运动的相关知识。通过多个例题解析了如何根据运动方程求解速度、加速度和轨迹方程,展示了从运动方程到实际物理现象的推导过程。
















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








