- 简单线性回归模型举例:
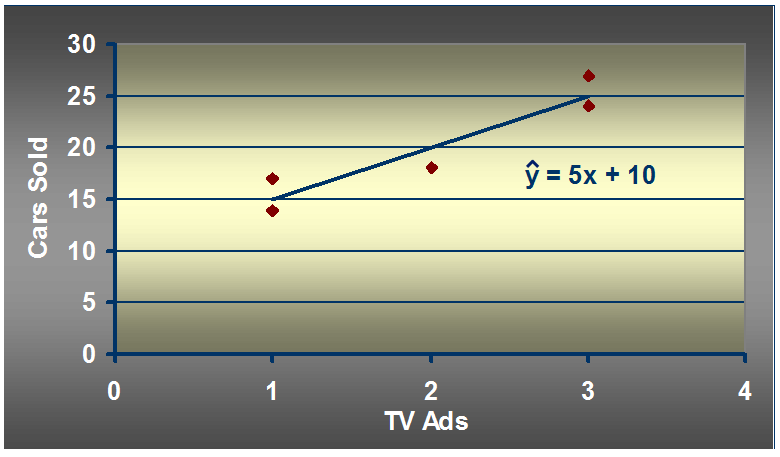
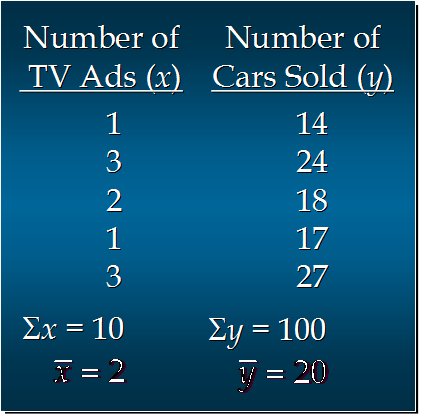
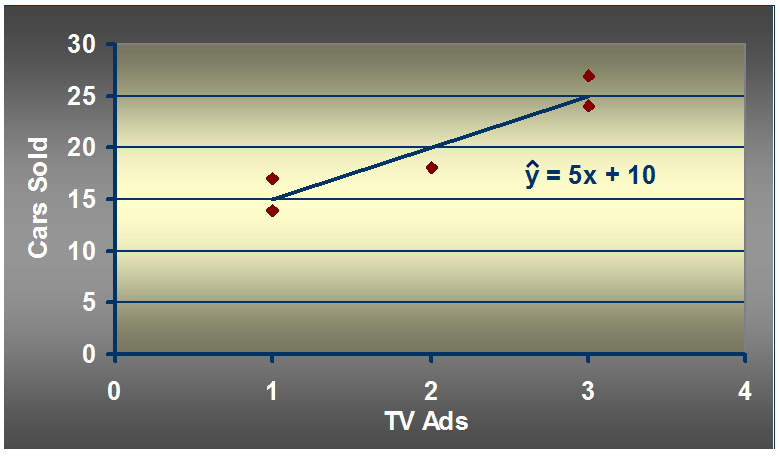
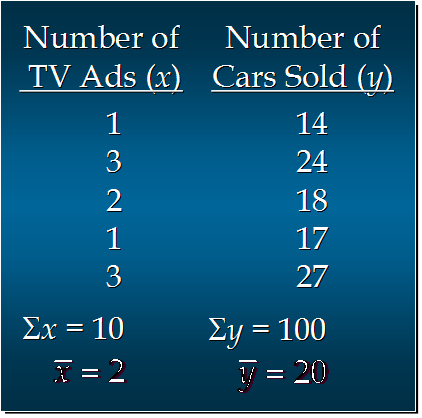
汽车卖家做电视广告数量与卖出的汽车数量:
1.1 如何练处适合简单线性回归模型的最佳回归线?
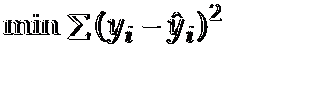
使sum of squares最小
1.1.2 计算
分子 = (1-2)(14-20)+(3-2)(24-20)+(2-2)(18-20)+(1-2)(17-20)+(3-2)(27-20)
= 6 + 4 + 0 + 3 + 7
= 20
分母 = (1-2)^2 + (3-2)^2 + (2-2)^2 + (1-2)^2 + (3-2)^2
= 1 + 1 + 0 + 1 + 1
4
b1 = 20/4 =5
b0 = 20 - 5*2 = 20 - 10 = 10
1.2 预测:
假设有一周广告数量为6,预测的汽车销售量是多少?
x_given = 6
Y_hat = 5*6 + 10 = 40
1.3 Python实现:
# -*- encoding=utf-8 -*-
#简单现行回归:只有一个自变量 y=k*x+b 预测使 (y-y*)^2 最小
import numpy as np
def fitSLR(x,y):
dinominator,numerator=0,0
for i in range(len(x)):
numerator+=(x[i]-np.mean(x))*(y[i]-np.mean(y))
dinominator+=(x[i]-np.mean(x))**2
print("numerator:" + str(numerator))
print("dinominator:" + str(dinominator))
b1=numerator/float(dinominator)
b0=np.mean(y)-b1*(np.mean(x))
return b0,b1
def predict(x,b0,b1):
return b0+b1*x
x=[1,3,2,1,3]
y=[14,24,18,17,27]
b0,b1=fitSLR(x, y)
y_predict=predict(10, b0, b1);
print("y_prediect:"+str(y_predict))








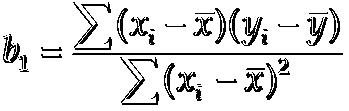
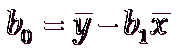
















 1159
1159

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








