class CV_EXPORTS_W KalmanFilter
{
public:
//! the default constructor
CV_WRAP KalmanFilter();
//! the full constructor taking the dimensionality of the state, of the measurement and of the control vector
CV_WRAP KalmanFilter(int dynamParams, int measureParams, int controlParams=0, int type=CV_32F);
//! re-initializes Kalman filter. The previous content is destroyed.
void init(int dynamParams, int measureParams, int controlParams=0, int type=CV_32F);
//! computes predicted state
CV_WRAP const Mat& predict(const Mat& control=Mat());
//! updates the predicted state from the measurement
CV_WRAP const Mat& correct(const Mat& measurement);
Mat statePre; //!< predicted state (x'(k)): x(k)=A*x(k-1)+B*u(k)
Mat statePost; //!< corrected state (x(k)): x(k)=x'(k)+K(k)*(z(k)-H*x'(k))
Mat transitionMatrix; //!< state transition matrix (A)
Mat controlMatrix; //!< control matrix (B) (not used if there is no control)
Mat measurementMatrix; //!< measurement matrix (H)
Mat processNoiseCov; //!< process noise covariance matrix (Q)
Mat measurementNoiseCov;//!< measurement noise covariance matrix (R)
Mat errorCovPre; //!< priori error estimate covariance matrix (P'(k)): P'(k)=A*P(k-1)*At + Q)*/
Mat gain; //!< Kalman gain matrix (K(k)): K(k)=P'(k)*Ht*inv(H*P'(k)*Ht+R)
Mat errorCovPost; //!< posteriori error estimate covariance matrix (P(k)): P(k)=(I-K(k)*H)*P'(k)
// temporary matrices
Mat temp1;
Mat temp2;
Mat temp3;
Mat temp4;
Mat temp5;
};// KalmanFilter.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include "opencv2/video/tracking.hpp"
#include "opencv2/highgui/highgui.hpp"
#include <stdio.h>
using namespace cv;
static inline Point calcPoint(Point2f center, double R, double angle)
{
return center + Point2f((float)cos(angle), (float)-sin(angle))*(float)R;
}
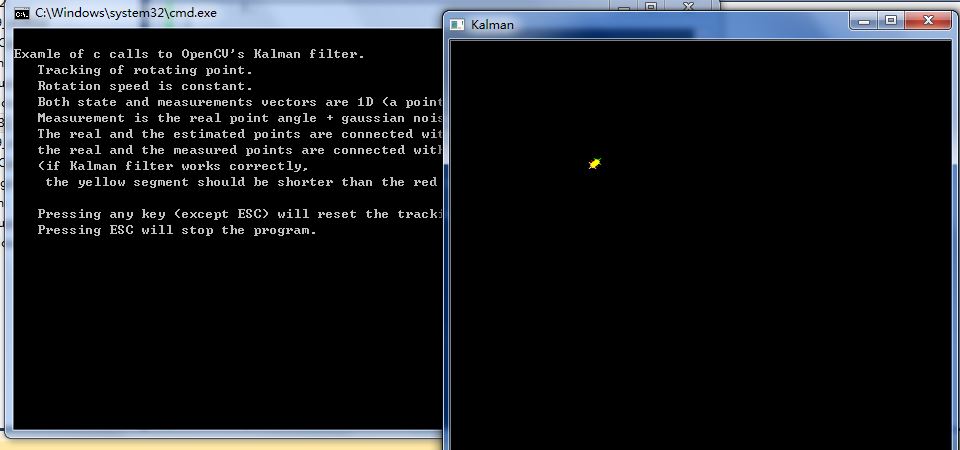
static void help()
{
printf( "\nExamle of c calls to OpenCV's Kalman filter.\n"
" Tracking of rotating point.\n"
" Rotation speed is constant.\n"
" Both state and measurements vectors are 1D (a point angle),\n"
" Measurement is the real point angle + gaussian noise.\n"
" The real and the estimated points are connected with yellow line segment,\n"
" the real and the measured points are connected with red line segment.\n"
" (if Kalman filter works correctly,\n"
" the yellow segment should be shorter than the red one).\n"
"\n"
" Pressing any key (except ESC) will reset the tracking with a different speed.\n"
" Pressing ESC will stop the program.\n"
);
}
int main(int, char**)
{
help();
Mat img(500, 500, CV_8UC3);
KalmanFilter KF(2, 1, 0);
Mat state(2, 1, CV_32F); /* (phi, delta_phi) */
Mat processNoise(2, 1, CV_32F);
Mat measurement = Mat::zeros(1, 1, CV_32F);
char code = (char)-1;
for(;;)
{
randn( state, Scalar::all(0), Scalar::all(0.1) );
KF.transitionMatrix = *(Mat_<float>(2, 2) << 1, 1, 0, 1);
setIdentity(KF.measurementMatrix);
setIdentity(KF.processNoiseCov, Scalar::all(1e-5));
setIdentity(KF.measurementNoiseCov, Scalar::all(1e-1));
setIdentity(KF.errorCovPost, Scalar::all(1));
randn(KF.statePost, Scalar::all(0), Scalar::all(0.1));
for(;;)
{
Point2f center(img.cols*0.5f, img.rows*0.5f);
float R = img.cols/3.f;
double stateAngle = state.at<float>(0);
Point statePt = calcPoint(center, R, stateAngle);
Mat prediction = KF.predict();
double predictAngle = prediction.at<float>(0);
Point predictPt = calcPoint(center, R, predictAngle);
randn( measurement, Scalar::all(0), Scalar::all(KF.measurementNoiseCov.at<float>(0)));
// generate measurement
measurement += KF.measurementMatrix*state;
double measAngle = measurement.at<float>(0);
Point measPt = calcPoint(center, R, measAngle);
// plot points
#define drawCross( center, color, d ) \
line( img, Point( center.x - d, center.y - d ), \
Point( center.x + d, center.y + d ), color, 1, CV_AA, 0); \
line( img, Point( center.x + d, center.y - d ), \
Point( center.x - d, center.y + d ), color, 1, CV_AA, 0 )
img = Scalar::all(0);
drawCross( statePt, Scalar(255,255,255), 3 );
drawCross( measPt, Scalar(0,0,255), 3 );
drawCross( predictPt, Scalar(0,255,0), 3 );
line( img, statePt, measPt, Scalar(0,0,255), 3, CV_AA, 0 );
line( img, statePt, predictPt, Scalar(0,255,255), 3, CV_AA, 0 );
if(theRNG().uniform(0,4) != 0)
KF.correct(measurement);
randn( processNoise, Scalar(0), Scalar::all(sqrt(KF.processNoiseCov.at<float>(0, 0))));
state = KF.transitionMatrix*state + processNoise;
imshow( "Kalman", img );
code = (char)waitKey(100);
if( code > 0 )
break;
}
if( code == 27 || code == 'q' || code == 'Q' )
break;
}
return 0;
}
下面的内容是转载:
原文:https://blog.csdn.net/onezeros/article/details/6318944
在机器视觉中追踪时常会用到预测算法,kalman是你一定知道的。它可以用来预测各种状态,比如说位置,速度等。关于它的理论有很多很好的文献可以参考。opencv给出了kalman filter的一个实现,而且有范例,但估计不少人对它的使用并不清楚,因为我也是其中一个。本文的应用是对二维坐标进行预测和平滑
使用方法:
1、初始化
const int stateNum=4;//状态数,包括(x,y,dx,dy)坐标及速度(每次移动的距离)
const int measureNum=2;//观测量,能看到的是坐标值,当然也可以自己计算速度,但没必要
Kalman* kalman = cvCreateKalman( stateNum, measureNum, 0 );//state(x,y,detaX,detaY)
转移矩阵或者说增益矩阵的值好像有点莫名其妙
- float A[stateNum][stateNum] ={ //transition matrix
- 1,0,1,0,
- 0,1,0,1,
- 0,0,1,0,
- 0,0,0,1
- };
看下图就清楚了
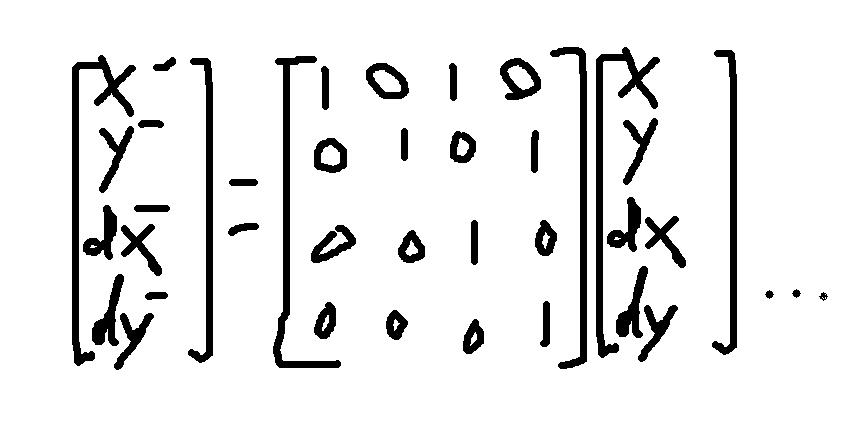
X1=X+dx,依次类推
所以这个矩阵还是很容易却确定的,可以根据自己的实际情况定制转移矩阵
同样的方法,三维坐标的转移矩阵可以如下





 本文介绍了如何在机器视觉中使用Kalman滤波器进行运动跟踪。通过初始化、预测、更新观测矩阵和更新Kalman滤波器,实现二维坐标预测和平滑。文章提供了一个简单的C++代码示例,展示如何应用Kalman滤波器预测鼠标移动轨迹。
本文介绍了如何在机器视觉中使用Kalman滤波器进行运动跟踪。通过初始化、预测、更新观测矩阵和更新Kalman滤波器,实现二维坐标预测和平滑。文章提供了一个简单的C++代码示例,展示如何应用Kalman滤波器预测鼠标移动轨迹。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








