一、 概述 Overview
1946年由Schoenberg提出了B样条理论,给出了B样条的差分表达式;1972年de Boor和Cox分别独立给出了关于B样条的标准算法。Gordon和Riesenfeld又把B样条理论用于形状描述,最终提出了B样条方法。用B样条基替代了Bernstein基,构造出B样条曲线,这种方法继承了Bezier方法的一切优点,克服了Bezier方法存在的缺点,较成功地解决了局部控制问题,又轻而易举地在参数连续性基础上解决了连接问题,从而使自由曲线曲面形状的描述问题得到较好解决。
p次B样条曲线的定义为:
其中:
Pi是控制顶点(control point);
Ni,p(u)是定义在非周期节点矢量上的p次B样条基函数;
有很多方法可以用来定义B样条基函数以及证明它的一些重要性质。例如,可以采用截尾幂函数的差商定义,开花定义,以及由de Boor和Cox等人提出的递推公式等来定义。我们这里采用的是递推定义方法,因为这种方法在计算机实现中是最有效的。
令U={u0,u1,…,um}是一个单调不减的实数序列,即ui<=ui+1,i=0,1,…,m-1。其中,ui称为节点,U称为节点矢量,用Ni,p(u)表示第i个p次B样条基函数,其定义为:
B样条基有如下性质:
a) 递推性;
b) 局部支承性;
c) 规范性;
d) 可微性;
根据B样条曲线定义可知,给定控制顶点Pi(control points),曲线次数p(degree)及节点矢量U(knot vectors),B样曲线也就确定。对于有理B样条曲线,还需要参数权重(weights)。
二、 OCC中的B样条曲线库 BSplCLib in OCC
在Open Cascade中的工具箱(Toolkit)TKMath中的包(package)BSplCLib是B样条曲线库,为B样条曲线曲面的计算提供了支持。它提供了三方面的功能:
对节点矢量(knot vectors)及重复度(multiplicities)的管理;
对多维样条的支持,即B样条方法中控制顶点的维数可以是任意维数(dimension);
二维和三维样条曲线的方法;
Open Cascade中的B样条曲线由下列数据项定义:
| 定义
| 变量类型
| 变量名称
|
| 控制顶点control points
| TColgp_Array1OfPnt
| Poles
|
| 权重weights
| TColStd_Array1OfReal
| Weights
|
| 节点knots
| TColStd_Array1OfReal
| Knots
|
| 重数multiplicities
| TColStd_Array1OfInteger
| Mults
|
| 次数degree
| Standard_Integer
| Degree
|
| 周期性periodicity
| Standard_Boolean
| Periodic
|
B样条曲线库BSplCLib提供了一些基本几何算法:
B样条基函数及其导数的计算BSplCLib::EvalBsplineBasis();
节点插入BSplCLib::InsertKnot();
节点去除BSplCLib::RemoveKnot();
升阶BSplCLib::IncreaseDegree();
降阶;
结合《The NURBS Book》和Open Cascade中的BSplCLib的源程序,可以高效的学习NURBS。《The NURBS Book》中有详细的理论推导及算法描述,而Open Cascade中有可以用来实际使用的程序。理论联系实际,有助于快速理解NURBS的有关概念及其应用。
---
opencascade-7.4.0\src\BSplCLib\BSplCLib.cxx
opencascade-7.4.0\inc\BSplCLib.hxx
//! The 3d or 2d B-spline curve is defined with :
//!
//! . its control points : TColgp_Array1OfPnt(2d) Poles
//! . its weights : TColStd_Array1OfReal Weights
//! . its knots : TColStd_Array1OfReal Knots
//! . its multiplicities : TColStd_Array1OfInteger Mults
//! . its degree : Standard_Integer Degree
//! . its periodicity : Standard_Boolean Periodic
//!
//! Warnings :
//! The bounds of Poles and Weights should be the same.
//! The bounds of Knots and Mults should be the same.
//!
//! Note: weight and multiplicity arrays can be passed by pointer for
//! some functions so that NULL pointer is valid.
//! That means no weights/no multiplicities passed.
//!
//! No weights (BSplCLib::NoWeights()) means the curve is non rational.
//! No mults (BSplCLib::NoMults()) means the knots are "flat" knots.








 本文深入探讨了B样条理论的历史背景、基本定义及其在OpenCascade中的实现方式,介绍了B样条曲线的构造原理,以及如何通过B样条基函数实现局部控制和参数连续性,同时涵盖了OCC中BSplCLib提供的关键算法。
本文深入探讨了B样条理论的历史背景、基本定义及其在OpenCascade中的实现方式,介绍了B样条曲线的构造原理,以及如何通过B样条基函数实现局部控制和参数连续性,同时涵盖了OCC中BSplCLib提供的关键算法。
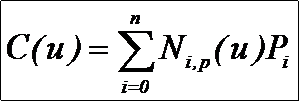

















 9230
9230

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








