目录
PQ(乘积量化)，说白了就是将向量分段量化，每一段分别聚类。一个向量由多个子段组合而成。上图：
PQ通过分段量化，也和SQ一样缩减了向量的存储成本。除此之外，PQ还有一些有别于SQ的独特优势，本文将展开介绍。
1. PQ类基本结构
struct ProductQuantizer {
size_t d; ///< size of the input vectors
size_t M; ///< number of subquantizers
size_t nbits; ///< number of bits per quantization index (jeven:no. of bits per segment)
// values derived from the above
size_t dsub; ///< dimensionality of each subvector = d/M
size_t code_size; ///< bytes per indexed vector = (nbits*M+7)/8 取整
size_t ksub; ///< number of centroids for each subquantizer = 1<<nbits
ClusteringParameters cp; ///< parameters used during clustering
/// Centroid table, size M * ksub * dsub (jeven:2维变1维，共M * ksub个中心点，每个中心点size维dsub)
std::vector<float> centroids;
}d: 向量总的维度
M: PQ分段数
nbits：每一个子段量化后的编码位数
后面三个变量都可以通过前面几个推导出来：
dsub: 每一个子段的维度，= d/M
code_size: 每一个向量编码所需的字节数，(nbits*M+7)/8
ksub: 每一个子段量化的中心数，=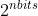
,也就是 1<<nbits
cp: 聚类的一些参数
centroids：存储每个子段的聚类中心的，多个子段，每个子段有多个中心，所以这里其实是二维数组，采用一维数组表示。总的中心数是M*ksub，每一段是ksub个。
2. 初始化
初始化其实就是根据d,M,nbits设置其他相关的参数：
ProductQuantizer::ProductQuantizer (size_t d, size_t M, size_t nbits):
d(d), M(M), nbits(nbits), assign_index(nullptr)
{
set_derived_values ();
}
void ProductQuantizer::set_derived_values () {
dsub = d / M;
code_size = (nbits * M + 7) / 8;
ksub = 1 << nbits;
centroids.resize (d * ksub);
verbose = false;
train_type = Train_default;
}3. 训练
训练，将各子段分别进行聚类，得到各子段的聚类中心。
float * xslice = new float[n * dsub];
for (int m = 0; m < M; m++) {
for (int j = 0; j < n; j++)
memcpy (xslice + j * dsub,
x + j * d + m * dsub, // jeven: subvector m of vector j
dsub * sizeof(float));
Clustering clus (dsub, ksub, cp);
IndexFlatL2 index (dsub);
clus.train (n, xslice, assign_index ? *assign_index : index);
// jeven: put clustering centeroids of m sgement into centeroids
set_params (clus.centroids.data(), m);
}以上是PQ.train的主体，两层循环，外层循环遍历每个子段，内层循环遍历并得到训练数据集的第j个子段。实例化一个聚类，然后训练，前面的文章我们聊过，训练其实就是聚类，找到各聚类的中心点。
所以这里就是我们找到每个子段的聚类中心，再通过set_params函数拷贝到PQ的成员变量centroids里：
// jeven: set the centroids of m-th segment
void ProductQuantizer::set_params (const float * centroids_, int m)
{
memcpy (get_centroids(m, 0), centroids_, ksub * dsub * sizeof (centroids_[0]));
}
/// return the centroids associated with subvector m
float * get_centroids (size_t m, size_t i) {
return ¢roids [(m * ksub + i) * dsub]; // jeven: return the ith centroid of m-th segment
}get_centroids(i, j)表示第i的子段的第j个聚类中心。
4. 搜索
假设我们要找向量x的近邻向量，PQ搜索的步骤为：首先将x也按照PQ规则分成M段，然后计算x的每一个子向量到该子段的ksub个聚类中心的距离，得到一个距离表，我们称之为码本。M段，所以码本的规模为M*ksub。当我们计算x与某一个向量y的距离时，首先得到x与y每个子段的距离，最后求和。如何计算子段的距离？因为y是数据集里面的，我们事先已经按照PQ的规则将其量化并得到了其各子段所属的聚类中心。所以这里可以分别查找y的各个子段所在聚类中心点，然后在对应的码本中找到x的某段子向量到y的子向量对应聚类中心的距离，视为x与y的该子段距离。
首先，如果没有分段，那么聚类中心的数量为1<<M*nbits=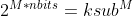
个，码本的规模也就是
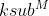个，而PQ所需的码本规模为M*ksub。
然后，对于距离的计算，我们用x到聚类中心的距离近似替代x到该中心下的向量的距离，将计算距离变成了查找距离。
下面一起看看faiss的具体实现。
/** perform a search (L2 distance)
* @param x query vectors, size nx * d
* @param nx nb of queries
* @param codes database codes, size ncodes * code_size
* @param ncodes nb of nb vectors
* @param res heap array to store results (nh == nx)
* @param init_finalize_heap initialize heap (input) and sort (output)?
*/
void search (const float * x,
size_t nx,
const uint8_t * codes,
const size_t ncodes,
float_maxheap_array_t *res,
bool init_finalize_heap = true) const
{
std::unique_ptr<float[]> dis_tables(new float [nx * ksub * M]);
compute_distance_tables (nx, x, dis_tables.get());
pq_knn_search_with_tables<CMax<float, int64_t>> (
*this, nbits, dis_tables.get(), codes, ncodes, res, init_finalize_heap);
}主要分两步：
1. 计算码本；
2. 从码本中查找距离。
4.1 计算码本
void ProductQuantizer::compute_distance_table (const float * x,
float * dis_table) const
{
size_t m;
// jeven: compute the dis between x_m and c_m,j
for (m = 0; m < M; m++) {
//jeven: in each loop, compute x_m and [c_m,0-c_m,k_sub]
fvec_L2sqr_ny (dis_table + m * ksub,
x + m * dsub,
get_centroids(m, 0),
dsub,
ksub);
}
}
void fvec_L2sqr_ny (float * dis, const float * x,
const float * y, size_t d, size_t ny) {
fvec_L2sqr_ny_ref (dis, x, y, d, ny);
}
void fvec_L2sqr_ny_ref (float * dis,
const float * x,
const float * y,
size_t d, size_t ny)
{
for (size_t i = 0; i < ny; i++) {
dis[i] = fvec_L2sqr (x, y, d);
y += d;
}
}compute_distance_table分别遍历每个子段，计算x的子向量到对应子段的ksub个中心的距离，并填入dis_table中。
在函数fvec_L2sqr_ny_ref中，分别计算x_m 到m子段的每个聚类中心的距离，存储在dis中。
4.2 从码本中查找距离
查找距离的函数为pq_knn_search_with_tables，利用堆从码本dis_table里面查找最近的向量。
template <class C>
static void pq_knn_search_with_tables (
const ProductQuantizer& pq,
size_t nbits,
const float *dis_tables,
const uint8_t * codes,
const size_t ncodes,
HeapArray<C> * res,
bool init_finalize_heap)
{
size_t k = res->k, nx = res->nh;
size_t ksub = pq.ksub, M = pq.M;
#pragma omp parallel for // jeven: 并行计算每个每个向量的近邻
for (int64_t i = 0; i < nx; i++) {
/* query preparation for asymmetric search: compute look-up tables */
const float* dis_table = dis_tables + i * ksub * M; // jeven: 获取第i个向量的码本
/* Compute distances and keep smallest values */
int64_t * __restrict heap_ids = res->ids + i * k;
float * __restrict heap_dis = res->val + i * k;
if (init_finalize_heap) {
heap_heapify<C> (k, heap_dis, heap_ids); //jeven: 堆初始化，heap_dis以距离来比较大小做堆的一些操作，heap_ids则为heap_dis中每个元素的对应id
}
switch (nbits) {
case 8:
pq_estimators_from_tables<uint8_t, C> (pq,
codes, ncodes,
dis_table,
k, heap_dis, heap_ids);
break;
case 16:
pq_estimators_from_tables<uint16_t, C> (pq,
(uint16_t*)codes, ncodes,
dis_table,
k, heap_dis, heap_ids);
break;
default:
pq_estimators_from_tables_generic<C> (pq,
nbits,
codes, ncodes,
dis_table,
k, heap_dis, heap_ids);
break;
}
if (init_finalize_heap) {
heap_reorder<C> (k, heap_dis, heap_ids);
}
}
}Faiss中查找距离表，根据nbits的大小分别选用了不同的函数去查找码本，原理都一样，分别遍历数据集中的每条数据的编码（其实是各子段所属中心id组合而成），查找各子段距离之和，再放入堆中，最后堆中剩下的那些元素就是搜索的结果。
5 总结
PQ的原理介绍完了，它的优化主要是三个方面：
1. 编码存储，空间成本的优化；
2. 码本规模的减小；
3. 将距离计算的复杂度由(n, 数据集的规模)变成了（M*ksub次计算的时间+查距离表的时间）。
扫一扫
3044
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
