tensorflow中的正则化解决过拟合问题

最新推荐文章于 2022-09-02 16:35:24 发布

lilong117194

最新推荐文章于 2022-09-02 16:35:24 发布

阅读量1.2w

点赞数 4

分类专栏： Tensorflow 文章标签： tensorflow 正则化范数

本文链接：https://blog.csdn.net/lilong117194/article/details/79130032

版权

Tensorflow 专栏收录该内容

22 篇文章 1 订阅

订阅专栏

1. 正则化

所谓的过拟合问题指的是当一个模型很复杂时，它可以很好的“记忆”每一个训练数据中的随机噪音的部分而忘记了要去“学习”训练数据中通用的趋势。

为了避免过拟合问题，一个非常常用的方法就是正则化。也就是在损失函数中加入刻画模型复杂程度的指标。假设用于损失函数的为 $J(\theta)$ ，那此时不直接优化 $J(\theta)$ ，而是优化 $J(\theta)+\lambda R(w)$ 。其中 $R(w)$ 刻画的是模型的复杂度，而 $\lambda$ 表示的是模型复杂损失在总损失中的比例。这里的 $\theta$ 表示的是一个神经网络中所有的参数，它包括边上的权重 $w$ 和偏置项 $b$ 。一般来说模型复杂度只由权重表示。常用的刻画模型复杂度的函数 $R(w)$ 有两种，一种是L1正则化，另一种是L2正则化。这两种都是通过限制权重的大小，使得模型不能任意拟合训练数据中的随机噪声。这两种正则化的区别是首先L1正则化会让参数变得稀疏（指会有更多参数变为0），而L2正则化则不会（因为参数的平方后会让小的参数变得更小，大的参数变得更大，同样起到了特征选取的功能，而不会让参数变为0）。其次是L1正则化计算不可导，而L2的正则化损失函数可导。

以上是一些简单的正则花基础，下面是神经网络的搭建：
当网络复杂的时候定义网络的结构部分和计算损失函数的部分可能不在一个函数中，这样通过简单的变量这种计算损失函数就不方便了。此时可以使用Tensorflow中提供的集合，它可以在一个计算图（tf.Graph）中保存一组实体（比如张量）。以下是通过集合计算一个5层的神经网络带L2正则化的损失函数的计算过程。

2. 基于tensorflow的代码实现

下面都是基于jupyter notebook 的代码：

生成模拟数据集。

import tensorflow as tf
import matplotlib.pyplot as plt 
import numpy as np

data = []
label = []
np.random.seed(0) # 设置随机数生成时所用算法开始的整数值

# 以原点为圆心，半径为1的圆把散点划分成红蓝两部分，并加入随机噪音。
for i in range(150):
    x1 = np.random.uniform(-1,1)  # 随机生成下一个实数，它在 [-1，1) 范围内。
    x2 = np.random.uniform(0,2)
    if x1**2 + x2**2 <= 1:
        data.append([np.random.normal(x1, 0.1),np.random.normal(x2,0.1)])
        label.append(0)
    else:
        data.append([np.random.normal(x1, 0.1), np.random.normal(x2, 0.1)])
        label.append(1)

data = np.hstack(data).reshape(-1,2) # 把数据转换成n行2列
label = np.hstack(label).reshape(-1, 1)  # 把数据转换为n行1列
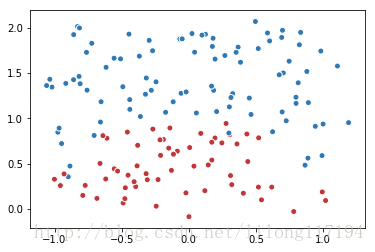
plt.scatter(data[:,0], data[:,1], c=label,cmap="RdBu", vmin=-.2, vmax=1.2, edgecolor="white")
plt.show()

结果：
这里写图片描述

#2. 定义一个获取权重，并自动加入正则项到损失的函数。
def get_weight(shape, lambda1):
    var = tf.Variable(tf.random_normal(shape), dtype=tf.float32) # 生成一个变量
    tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(lambda1)(var)) # add_to_collection()函数将新生成变量的L2正则化损失加入集合losses
    return var # 返回生成的变量

#3. 定义神经网络。
x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))
sample_size = len(data)

# 每层节点的个数
layer_dimension = [2,10,5,3,1]
# 神经网络的层数
n_layers = len(layer_dimension)
# 这个变量维护前向传播时最深层的节点，开始的时候就是输入层
cur_layer = x
# 当前层的节点个数
in_dimension = layer_dimension[0]

# 循环生成网络结构
for i in range(1, n_layers):
    out_dimension = layer_dimension[i] # layer_dimension[i]为下一层的节点个数
    # 生成当前层中权重的变量，并将这个变量的L2正则化损失加入计算图上的集合
    weight = get_weight([in_dimension, out_dimension], 0.003)
    bias = tf.Variable(tf.constant(0.1, shape=[out_dimension])) # 偏置
    cur_layer = tf.nn.relu(tf.matmul(cur_layer, weight) + bias) # 使用Relu激活函数
    in_dimension = layer_dimension[i]  # 进入下一层之前将下一层的节点个数更新为当前节点个数

y= cur_layer

# 在定义神经网络前向传播的同时已经将所有的L2正则化损失加入了图上的集合，这里是损失函数的定义。
mse_loss = tf.reduce_sum(tf.pow(y_ - y, 2)) / sample_size # 也可以写成：tf.reduce_mean(tf.square(y_ - y`))
tf.add_to_collection('losses', mse_loss) # 将均方误差损失函数加入损失集合
# get_collection()返回一个列表，这个列表是所有这个集合中的元素，在本样例中这些元素就是损失函数的不同部分，将他们加起来就是最终的损失函数
loss = tf.add_n(tf.get_collection('losses'))

# 4. 训练不带正则项的损失函数mse_loss。
# 定义训练的目标函数mse_loss，训练次数及训练模型
train_op = tf.train.AdamOptimizer(0.001).minimize(mse_loss)
TRAINING_STEPS = 40000

with tf.Session() as sess:
    tf.global_variables_initializer().run() # 初始化所有的变量
    for i in range(TRAINING_STEPS):
        sess.run(train_op, feed_dict={x: data, y_: label})
        if i % 2000 == 0:
            print("After %d steps, mse_loss: %f" % (i,sess.run(mse_loss, feed_dict={x: data, y_: label})))

    # 画出训练后的分割曲线       
    xx, yy = np.mgrid[-1.2:1.2:.01, -0.2:2.2:.01]
    grid = np.c_[xx.ravel(), yy.ravel()]
    probs = sess.run(y, feed_dict={x:grid})
    probs = probs.reshape(xx.shape)

plt.scatter(data[:,0], data[:,1], c=label, cmap="RdBu", vmin=-.2, vmax=1.2, edgecolor="white")
plt.contour(xx, yy, probs, levels=[.5], cmap="Greys", vmin=0, vmax=.1)
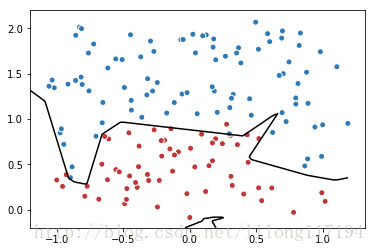
plt.show()

运行结果：

After 0 steps, mse_loss: 0.588501
After 2000 steps, mse_loss: 0.039796
After 4000 steps, mse_loss: 0.018524
After 6000 steps, mse_loss: 0.018494
After 8000 steps, mse_loss: 0.018374
After 10000 steps, mse_loss: 0.018358
After 12000 steps, mse_loss: 0.018356
After 14000 steps, mse_loss: 0.018355
After 16000 steps, mse_loss: 0.016440
After 18000 steps, mse_loss: 0.013988
After 20000 steps, mse_loss: 0.013142
After 22000 steps, mse_loss: 0.012886
After 24000 steps, mse_loss: 0.012700
After 26000 steps, mse_loss: 0.012550
After 28000 steps, mse_loss: 0.006441
After 30000 steps, mse_loss: 0.006439
After 32000 steps, mse_loss: 0.006438
After 34000 steps, mse_loss: 0.006438
After 36000 steps, mse_loss: 0.006445
After 38000 steps, mse_loss: 0.006438

这里写图片描述

#5. 训练带正则项的损失函数loss。
# 定义训练的目标函数loss，训练次数及训练模型
train_op = tf.train.AdamOptimizer(0.001).minimize(loss)
TRAINING_STEPS = 40000

with tf.Session() as sess:
    tf.global_variables_initializer().run()
    for i in range(TRAINING_STEPS):
        sess.run(train_op, feed_dict={x: data, y_: label})
        if i % 2000 == 0:
            print("After %d steps, loss: %f" % (i, sess.run(loss, feed_dict={x: data, y_: label})))

    # 画出训练后的分割曲线       
    xx, yy = np.mgrid[-1:1:.01, 0:2:.01]
    grid = np.c_[xx.ravel(), yy.ravel()]
    probs = sess.run(y, feed_dict={x:grid})
    probs = probs.reshape(xx.shape)

plt.scatter(data[:,0], data[:,1], c=label,cmap="RdBu", vmin=-.2, vmax=1.2, edgecolor="white")
plt.contour(xx, yy, probs, levels=[.5], cmap="Greys", vmin=0, vmax=.1)
plt.show()

运行结果：

After 0 steps, loss: 0.705000
After 2000 steps, loss: 0.056949
After 4000 steps, loss: 0.045995
After 6000 steps, loss: 0.041472
After 8000 steps, loss: 0.040165
After 10000 steps, loss: 0.039961
After 12000 steps, loss: 0.039916
After 14000 steps, loss: 0.039912
After 16000 steps, loss: 0.039912
After 18000 steps, loss: 0.038334
After 20000 steps, loss: 0.038128
After 22000 steps, loss: 0.037962
After 24000 steps, loss: 0.037932
After 26000 steps, loss: 0.037921
After 28000 steps, loss: 0.037918
After 30000 steps, loss: 0.037910
After 32000 steps, loss: 0.037908
After 34000 steps, loss: 0.037910
After 36000 steps, loss: 0.037907
After 38000 steps, loss: 0.037905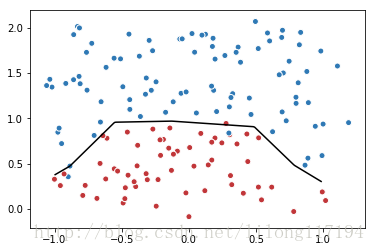

这里写图片描述
以上是代码的具体运行过程和运行结果。

3. 笔记

3.1 numpy.random.seed()的使用：

seed() 方法改变随机数生成器的种子，可以在调用其他随机模块函数之前调用此函数。
seed( ) 用于指定随机数生成时所用算法开始的整数值，如果使用相同的seed( )值，则每次生成的随即数都相同，如果不设置这个值，则系统根据时间来自己选择这个值，此时每次生成的随机数因时间差异而不同。

示例（1）：

from numpy import *
num=0
while(num<5):
    random.seed(5)
    print(random.random())
    num+=1

运行结果：

0.22199317108973948
0.22199317108973948
0.22199317108973948
0.22199317108973948
0.22199317108973948

示例（2）：

from numpy import *
num=0
random.seed(5)
while(num<5):
    print(random.random())
    num+=1

运行结果：

0.22199317108973948
0.8707323061773764
0.20671915533942642
0.9186109079379216
0.48841118879482914

示例（3）：

import numpy as np

np.random.seed(0) 
x1 = np.random.uniform(-1,1)
print 'x1:',x1
np.random.seed(0)  
num=0
while(num<5):
    print(np.random.uniform(-1,1))
    num+=1

运行结果：

x1: 0.0976270078546
0.0976270078546
0.430378732745
0.205526752143
0.0897663659938
-0.152690401322

这里要注意的是设置的seed()值仅一次有效，从前两行的运行结果和以后的运行结果可以看出来。

3.2 Python uniform() 函数

uniform()是不能直接访问的，需要导入 random 模块，然后通过 random 静态对象调用该方法。

import random
random.uniform(x, y)

uniform() 方法将随机生成下一个实数，它在 [x, y) 范围内。

x – 随机数的最小值，包含该值。
y – 随机数的最大值，不包含该值。
返回一个浮点数。

注：
还有一种写法：numpy.random.uniform(low,high,size)
从一个均匀分布[low,high)中随机采样，注意定义域是左闭右开，即包含low，不包含high。
参数介绍:

low: 采样下界，float类型，默认值为0；
high: 采样上界，float类型，默认值为1；
size: 输出样本数目，为int或元组(tuple)类型，例如，size=(m,n,k), 则输出m*n*k个样本，缺省时输出1个值。

3.3 tf.placeholder 与 tf.Variable

tf.Variable：主要在于一些可训练变量（trainable variables），比如模型的权重（weights，W）或者偏执值（bias）；

(1)声明时，必须提供初始值；
(2)名称的真实含义，在于变量，也即在真实训练时，其值是会改变的，自然事先需要指定初始值；
tf.placeholder：用于得到传递进来的真实的训练样本：

（1）不必指定初始值，可在运行时，通过 Session.run 的函数的 feed_dict 参数指定；
（2）这也是其命名的原因所在，仅仅作为一种占位符；

3.4 `ImportError: No module named matplotlib.pyplot`错误

这里给出具体的解决办法

参考：http://blog.csdn.net/lanchunhui/article/details/61712830
http://blog.csdn.net/linzch3/article/details/58220569
《tensorflow实战google深度学习框架》

lilong117194

关注

4
点赞
踩
34

收藏

觉得还不错? 一键收藏
3
评论
tensorflow中的正则化解决过拟合问题

1. 正则化所谓的过拟合问题指的是当一个模型很复杂时，它可以很好的“记忆”每一个训练数据中的随机噪音的部分而忘记了要去“学习”训练数据中通用的趋势。为了避免过拟合问题，一个非常常用的方法就是正则化。也就是在损失函数中加入刻画模型复杂程度的指标。假设用于损失函数的为J(θ)J(\theta)，那此时不直接优化J(θ)J(\theta)，而是优化J(θ)+λR(w)J(\theta)+\lam
复制链接

扫一扫