ReLU激活函数详解：原理、应用与实现

原创 已于 2025-11-15 11:18:53 修改 · 711 阅读 · 7 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#人工智能 #tensorflow #神经网络

于 2025-11-14 08:41:21 首次发布

目录

1. ReLU激活函数概述

1.1 什么是激活函数？

1.2 ReLU的诞生背景

2. ReLU原理详解

2.1 基本数学定义

2.2 函数特性分析

2.2.1 输出范围

2.2.2 导数计算

2.3 可视化理解

3. ReLU的优势与局限性

3.1 主要优势

3.1.1 缓解梯度消失问题

3.1.2 计算效率极高

3.1.3 稀疏激活特性

3.2 主要局限性

3.2.1 死亡ReLU问题（Dying ReLU）

3.2.2 非零中心性

4. ReLU的变种改进

4.1 Leaky ReLU

4.2 主要变种对比

5. TensorFlow代码实现

5.1 基础ReLU实现

5.2 在神经网络中使用ReLU

5.3 完整训练示例

5.4 高级应用：自定义ReLU变种

6. ReLU应用场景

6.1 计算机视觉

6.2 自然语言处理

6.3 推荐系统

7. 实践建议与最佳实践

7.1 何时使用ReLU？

7.2 何时避免ReLU？

7.3 超参数调优建议

总结

1. ReLU激活函数概述

1.1 什么是激活函数？

激活函数是神经网络中的核心组件，它决定了神经元是否应该被"激活"，即是否将输入信号传递到下一层。激活函数为神经网络引入了非线性特性，使其能够学习复杂模式。

1.2 ReLU的诞生背景

在ReLU出现之前，神经网络主要使用Sigmoid和Tanh等激活函数。但这些函数存在梯度消失问题，限制了深层网络的训练效果。ReLU的提出彻底改变了这一局面。

2. ReLU原理详解

2.1 基本数学定义

ReLU（Rectified Linear Unit） 的数学表达式极其简单：

f(x) = max(0, x)

或者分段函数形式：

        { 0,  if x < 0
f(x) =  {
        { x,  if x ≥ 0

2.2 函数特性分析

2.2.1 输出范围

  • 输入为负：输出恒为0

  • 输入为非负：输出等于输入

  • 输出范围：[0, +∞)

2.2.2 导数计算

ReLU的导数同样简单：

        { 0,  if x < 0
f'(x) = {
        { 1,  if x > 0

在x=0处，导数理论上不存在，但在实际实现中通常将其定义为0或1。

2.3 可视化理解

import numpy as np
import matplotlib.pyplot as plt

def relu(x):
    return np.maximum(0, x)

def relu_derivative(x):
    return np.where(x > 0, 1, 0)

# 生成数据
x = np.linspace(-3, 3, 1000)
y_relu = relu(x)
y_derivative = relu_derivative(x)

# 绘制图形
plt.figure(figsize=(15, 5))

plt.subplot(1, 2, 1)
plt.plot(x, y_relu, 'b-', linewidth=2, label='ReLU')
plt.title('ReLU激活函数', fontsize=14)
plt.xlabel('x', fontsize=12)
plt.ylabel('f(x)', fontsize=12)
plt.grid(True, alpha=0.3)
plt.legend()

plt.subplot(1, 2, 2)
plt.plot(x, y_derivative, 'r-', linewidth=2, label='ReLU导数')
plt.title('ReLU导数', fontsize=14)
plt.xlabel('x', fontsize=12)
plt.ylabel("f'(x)", fontsize=12)
plt.grid(True, alpha=0.3)
plt.legend()

plt.tight_layout()
plt.show()

运行代码得到下图

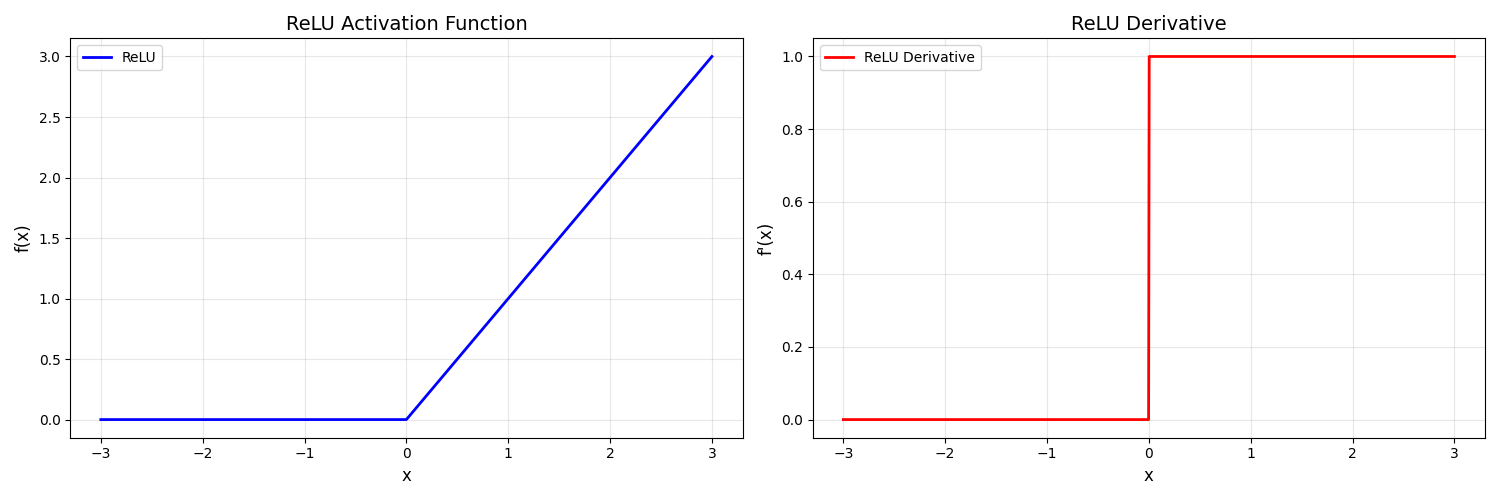
3. ReLU的优势与局限性

3.1 主要优势

3.1.1 缓解梯度消失问题
import numpy as np
import matplotlib.pyplot as plt

# ReLU函数定义
def relu(x):
    return np.maximum(0, x)

def relu_derivative_func(x):
    return np.where(x > 0, 1, 0)
 
# 对比不同激活函数的梯度
def compare_gradients():
    x = np.linspace(-5, 5, 1000)
    
    # Sigmoid及其导数
    sigmoid = 1 / (1 + np.exp(-x))
    sigmoid_derivative = sigmoid * (1 - sigmoid)
    
    # Tanh及其导数
    tanh_val = np.tanh(x)
    tanh_derivative = 1 - tanh_val**2
    
    # ReLU及其导数
    relu_val = relu(x)
    relu_derivative = relu_derivative_func(x)
    
    plt.figure(figsize=(12, 4))
    
    plt.subplot(1, 3, 1)
    plt.plot(x, sigmoid_derivative, 'r-', label='Sigmoid Derivative')
    plt.title('Sigmoid Derivative Range: (0, 0.25]')
    plt.grid(True, alpha=0.3)
    
    plt.subplot(1, 3, 2)
    plt.plot(x, tanh_derivative, 'g-', label='Tanh Derivative')
    plt.title('Tanh Derivative Range: (0, 1]')
    plt.grid(True, alpha=0.3)
    
    plt.subplot(1, 3, 3)
    plt.plot(x, relu_derivative, 'b-', label='ReLU Derivative')
    plt.title('ReLU Derivative Range: {0, 1}')
    plt.grid(True, alpha=0.3)
    plt.legend()
    
    plt.tight_layout()
    plt.show()

compare_gradients()

运行得到下图：

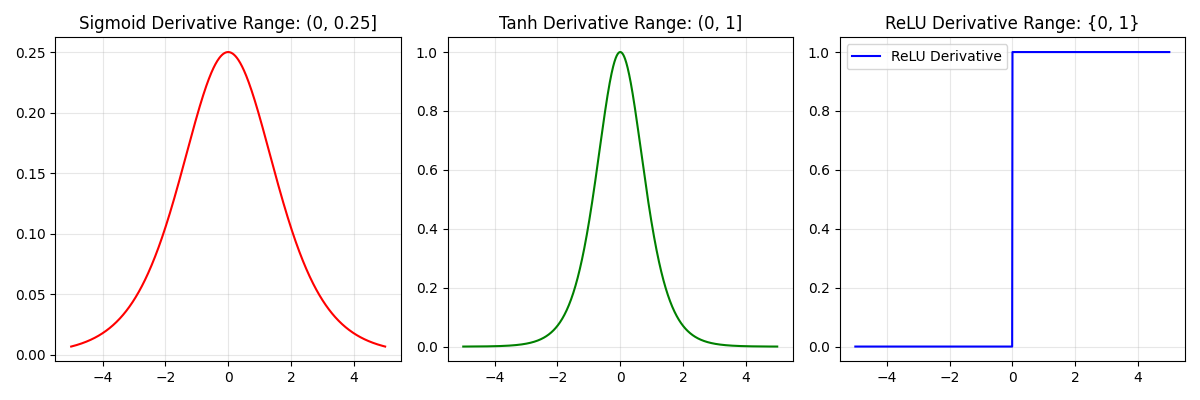
关键洞察：

  • Sigmoid导数最大为0.25，在深层网络中梯度会快速衰减

  • Tanh导数最大为1，但同样会衰减

  • ReLU在正区间的导数恒为1，彻底解决了梯度消失问题

3.1.2 计算效率极高

ReLU只涉及比较操作，没有指数、除法等复杂运算：

import time

def benchmark_activations():
    x = np.random.randn(1000000)
    
    # Sigmoid计算时间
    start = time.time()
    _ = 1 / (1 + np.exp(-x))
    sigmoid_time = time.time() - start
    
    # Tanh计算时间
    start = time.time()
    _ = np.tanh(x)
    tanh_time = time.time() - start
    
    # ReLU计算时间
    start = time.time()
    _ = np.maximum(0, x)
    relu_time = time.time() - start
    
    print(f"Sigmoid计算时间: {sigmoid_time:.6f}秒")
    print(f"Tanh计算时间: {tanh_time:.6f}秒")
    print(f"ReLU计算时间: {relu_time:.6f}秒")
    print(f"ReLU比Sigmoid快 {sigmoid_time/relu_time:.2f}倍")

benchmark_activations()
3.1.3 稀疏激活特性

ReLU的负半轴输出为0，使得网络具有稀疏性：

  • 只有约50%的神经元被激活

  • 减少参数间的相互依赖

  • 增强模型的泛化能力

3.2 主要局限性

3.2.1 死亡ReLU问题（Dying ReLU）
def demonstrate_dying_relu():
    """演示死亡ReLU问题"""
    # 模拟权重更新导致神经元永久死亡的情况
    weights = np.array([-2.0, -1.5, -0.5, 0.5, 1.0, 2.0])
    inputs = np.array([1.0, 0.5, -0.2, 0.3, -0.8, 0.1])
    
    # 前向传播
    outputs = np.maximum(0, weights * inputs)
    
    print("权重:", weights)
    print("输入:", inputs)
    print("加权和:", weights * inputs)
    print("ReLU输出:", outputs)
    print("死亡神经元数量:", np.sum(outputs == 0))

demonstrate_dying_relu()

死亡ReLU的原因：

  1. 学习率过大

  2. 权重初始化不当

  3. 较大的负偏置

3.2.2 非零中心性

ReLU的输出始终≥0，这可能导致：

  • 梯度更新方向单一

  • 训练过程可能震荡

  • 收敛速度受影响

4. ReLU的变种改进

4.1 Leaky ReLU

import numpy as np
import matplotlib.pyplot as plt

def relu(x):
    return np.maximum(0, x)

def leaky_relu(x, alpha=0.01):
    return np.where(x > 0, x, alpha * x)

def plot_relu_variants():
    x = np.linspace(-3, 3, 1000)
    
    plt.figure(figsize=(15, 10))
    
    # ReLU
    plt.subplot(2, 3, 1)
    plt.plot(x, relu(x), 'b-', linewidth=2)
    plt.title('Standard ReLU', fontsize=14)
    plt.grid(True, alpha=0.3)
    
    # Leaky ReLU
    plt.subplot(2, 3, 2)
    plt.plot(x, leaky_relu(x), 'g-', linewidth=2)
    plt.title('Leaky ReLU (α=0.01)', fontsize=14)
    plt.grid(True, alpha=0.3)
    
    # PReLU (可学习参数的Leaky ReLU)
    plt.subplot(2, 3, 3)
    for alpha in [0.1, 0.3, 0.5]:
        plt.plot(x, leaky_relu(x, alpha), label=f'α={alpha}')
    plt.title('PReLU (diffrent α)', fontsize=14)
    plt.legend()
    plt.grid(True, alpha=0.3)
    
    # ELU
    plt.subplot(2, 3, 4)
    elu = np.where(x > 0, x, 0.1 * (np.exp(x) - 1))
    plt.plot(x, elu, 'purple', linewidth=2)
    plt.title('ELU', fontsize=14)
    plt.grid(True, alpha=0.3)
    
    # SELU
    plt.subplot(2, 3, 5)
    lam = 1.0507
    alpha = 1.67326
    selu = np.where(x > 0, lam * x, lam * alpha * (np.exp(x) - 1))
    plt.plot(x, selu, 'orange', linewidth=2)
    plt.title('SELU', fontsize=14)
    plt.grid(True, alpha=0.3)
    
    # Swish
    plt.subplot(2, 3, 6)
    swish = x * (1 / (1 + np.exp(-x)))
    plt.plot(x, swish, 'red', linewidth=2)
    plt.title('Swish', fontsize=14)
    plt.grid(True, alpha=0.3)
    
    plt.tight_layout()
    plt.show()

plot_relu_variants()

运行得到下图：

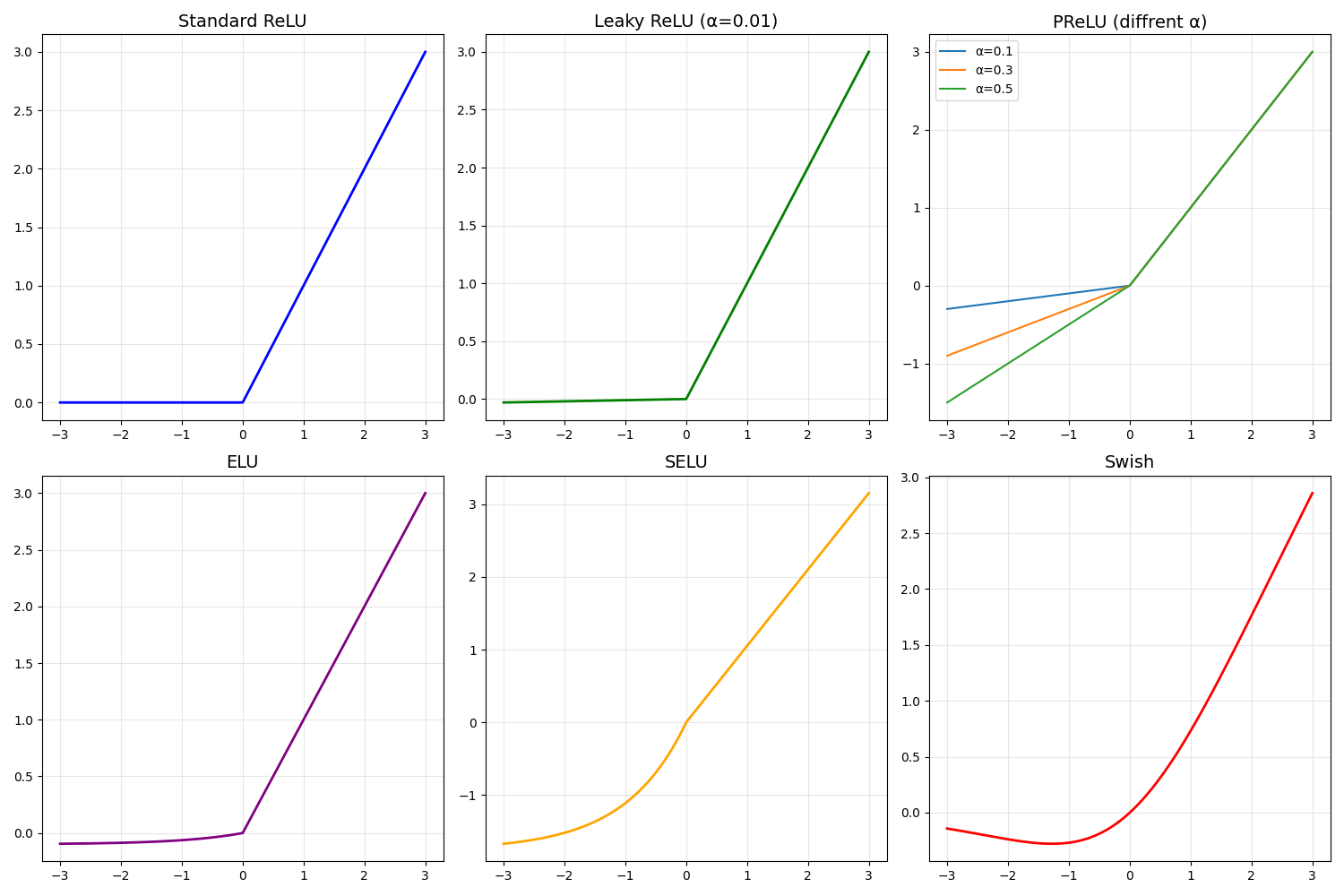
4.2 主要变种对比

变种名称

公式

优点

缺点

Leaky ReLU

max(αx, x)

解决死亡ReLU

需要调参

PReLU

max(αx, x)

α可学习

增加参数

ELU

x if x>0 else α(eˣ-1)

负区平滑

计算复杂

SELU

λ×ELU

自归一化

需要特定初始化

5. TensorFlow代码实现

5.1 基础ReLU实现

import tensorflow as tf
import numpy as np

class CustomReLU:
    """自定义ReLU实现"""
    
    @staticmethod
    def forward(x):
        """前向传播"""
        return tf.maximum(0.0, x)
    
    @staticmethod
    def backward(x, grad_output):
        """反向传播"""
        return tf.where(x > 0, grad_output, 0.0)

# 测试自定义ReLU
def test_custom_relu():
    # 创建测试数据
    x = tf.constant([-2.0, -1.0, 0.0, 1.0, 2.0])
    
    # 前向传播
    with tf.GradientTape() as tape:
        tape.watch(x)
        y = CustomReLU.forward(x)
    
    # 反向传播
    grad = tape.gradient(y, x)
    
    print("输入:", x.numpy())
    print("ReLU输出:", y.numpy())
    print("梯度:", grad.numpy())

test_custom_relu()

5.2 在神经网络中使用ReLU

def create_relu_network():
    """创建使用ReLU的神经网络"""
    
    # 方法1: 使用tf.nn.relu
    def create_with_tf_nn():
        model = tf.keras.Sequential([
            tf.keras.layers.Dense(128, input_shape=(784,)),
            tf.keras.layers.Lambda(lambda x: tf.nn.relu(x)),
            tf.keras.layers.Dense(64),
            tf.keras.layers.Lambda(lambda x: tf.nn.relu(x)),
            tf.keras.layers.Dense(10, activation='softmax')
        ])
        return model
    
    # 方法2: 直接在Dense层中指定activation
    def create_with_activation():
        model = tf.keras.Sequential([
            tf.keras.layers.Dense(128, activation='relu', input_shape=(784,)),
            tf.keras.layers.Dense(64, activation='relu'),
            tf.keras.layers.Dense(10, activation='softmax')
        ])
        return model
    
    # 方法3: 使用Leaky ReLU
    def create_with_leaky_relu():
        model = tf.keras.Sequential([
            tf.keras.layers.Dense(128, input_shape=(784,)),
            tf.keras.layers.LeakyReLU(alpha=0.01),
            tf.keras.layers.Dense(64),
            tf.keras.layers.LeakyReLU(alpha=0.01),
            tf.keras.layers.Dense(10, activation='softmax')
        ])
        return model
    
    # 方法4: 使用PReLU
    def create_with_prelu():
        model = tf.keras.Sequential([
            tf.keras.layers.Dense(128, input_shape=(784,)),
            tf.keras.layers.PReLU(),
            tf.keras.layers.Dense(64),
            tf.keras.layers.PReLU(),
            tf.keras.layers.Dense(10, activation='softmax')
        ])
        return model
    
    return {
        'tf_nn_relu': create_with_tf_nn(),
        'activation_relu': create_with_activation(),
        'leaky_relu': create_with_leaky_relu(),
        'prelu': create_with_prelu()
    }

# 创建并比较不同ReLU实现的网络
models = create_relu_network()
for name, model in models.items():
    print(f"{name}:")
    model.summary()
    print()

5.3 完整训练示例

import tensorflow as tf
import matplotlib.pyplot as plt

def train_with_relu_comparison():
    """比较不同ReLU变种的训练效果"""
    
    # 加载数据
    (x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
    
    # 数据预处理
    x_train = x_train.reshape(-1, 784).astype('float32') / 255.0
    x_test = x_test.reshape(-1, 784).astype('float32') / 255.0
    
    # 定义不同的激活函数
    activations = {
        'ReLU': 'relu',
        'LeakyReLU': tf.keras.layers.LeakyReLU(negative_slope=0.01),
        'PReLU': tf.keras.layers.PReLU(),
        'ELU': 'elu'
    }
    
    results = {}
    
    for name, activation in activations.items():
        print(f"\n训练使用 {name} 的模型...")
        
        # 创建模型
        model = tf.keras.Sequential()
        model.add(tf.keras.layers.Input(shape=(784,)))
        model.add(tf.keras.layers.Dense(128))
        
        # 处理激活函数 - 为PReLU创建独立实例
        if name == 'PReLU':
            model.add(tf.keras.layers.PReLU())
            model.add(tf.keras.layers.Dense(64))
            model.add(tf.keras.layers.PReLU())  # 新的独立实例
        else:
            # 其他激活函数的处理方式
            if isinstance(activation, str):
                model.add(tf.keras.layers.Activation(activation))
            else:
                model.add(activation)
            
            model.add(tf.keras.layers.Dense(64))
            
            # 再次添加激活函数
            if isinstance(activation, str):
                model.add(tf.keras.layers.Activation(activation))
            else:
                model.add(activation)
        
        model.add(tf.keras.layers.Dense(10, activation='softmax'))
        
        # 编译模型
        model.compile(
            optimizer='adam',
            loss='sparse_categorical_crossentropy',
            metrics=['accuracy']
        )
        
        # 训练模型
        history = model.fit(
            x_train, y_train,
            batch_size=128,
            epochs=10,
            validation_split=0.2,
            verbose=0
        )
        
        # 评估模型
        test_loss, test_accuracy = model.evaluate(x_test, y_test, verbose=0)
        
        results[name] = {
            'history': history,
            'test_accuracy': test_accuracy,
            'test_loss': test_loss
        }
        
        print(f"{name} - 测试准确率: {test_accuracy:.4f}")
    
    return results

def plot_comparison_results(results):
    """绘制比较结果"""
    plt.figure(figsize=(15, 5))
    
    # 训练准确率
    plt.subplot(1, 2, 1)
    for name, result in results.items():
        plt.plot(result['history'].history['accuracy'], 
                label=f'{name}', linewidth=2)
    plt.title('Training Accuracy Comparison')
    plt.xlabel('Epoch')
    plt.ylabel('Accuracy')
    plt.legend()
    plt.grid(True, alpha=0.3)
    
    # 测试准确率比较
    plt.subplot(1, 2, 2)
    names = list(results.keys())
    accuracies = [results[name]['test_accuracy'] for name in names]
    
    bars = plt.bar(names, accuracies, color=['blue', 'green', 'orange', 'red'])
    plt.title('Test Accuracy Comparison')
    plt.ylabel('Accuracy')
    
    # 在柱状图上显示数值
    for bar, accuracy in zip(bars, accuracies):
        plt.text(bar.get_x() + bar.get_width()/2, bar.get_height() + 0.001,
                f'{accuracy:.4f}', ha='center', va='bottom')
    
    plt.tight_layout()
    plt.show()

# 运行比较实验
results = train_with_relu_comparison()
plot_comparison_results(results)

运行结果如下：

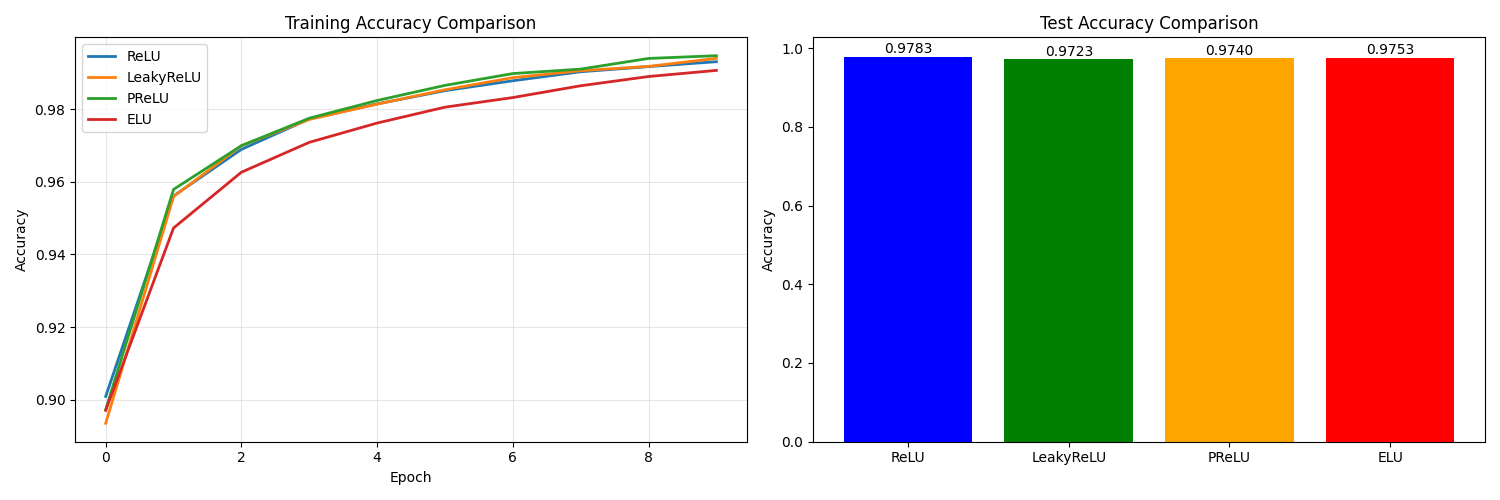
5.4 高级应用：自定义ReLU变种

class LearnableReLU(tf.keras.layers.Layer):
    """可学习参数的ReLU变种"""
    
    def __init__(self, initial_alpha=0.01, **kwargs):
        super(LearnableReLU, self).__init__(**kwargs)
        self.initial_alpha = initial_alpha
    
    def build(self, input_shape):
        self.alpha = self.add_weight(
            name='alpha',
            shape=(1,),
            initializer=tf.constant_initializer(self.initial_alpha),
            trainable=True
        )
        super(LearnableReLU, self).build(input_shape)
    
    def call(self, inputs):
        positive = tf.nn.relu(inputs)
        negative = self.alpha * (inputs - tf.abs(inputs)) * 0.5
        return positive + negative
    
    def get_config(self):
        config = super(LearnableReLU, self).get_config()
        config.update({'initial_alpha': self.initial_alpha})
        return config

# 使用自定义LearnableReLU
def create_advanced_network():
    model = tf.keras.Sequential([
        tf.keras.layers.Dense(128, input_shape=(784,)),
        LearnableReLU(initial_alpha=0.1),
        tf.keras.layers.Dense(64),
        LearnableReLU(initial_alpha=0.1),
        tf.keras.layers.Dense(10, activation='softmax')
    ])
    return model

# 测试自定义层
def test_learnable_relu():
    layer = LearnableReLU(initial_alpha=0.1)
    test_input = tf.constant([-2.0, -1.0, 0.0, 1.0, 2.0])
    output = layer(test_input)
    
    print("输入:", test_input.numpy())
    print("输出:", output.numpy())
    print("可学习参数alpha:", layer.alpha.numpy())

test_learnable_relu()

6. ReLU应用场景

6.1 计算机视觉

def relu_in_cnn():
    """CNN中的ReLU应用"""
    model = tf.keras.Sequential([
        # 卷积层 + ReLU
        tf.keras.layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)),
        tf.keras.layers.MaxPooling2D((2, 2)),
        
        tf.keras.layers.Conv2D(64, (3, 3), activation='relu'),
        tf.keras.layers.MaxPooling2D((2, 2)),
        
        tf.keras.layers.Conv2D(64, (3, 3), activation='relu'),
        tf.keras.layers.Flatten(),
        
        # 全连接层 + ReLU
        tf.keras.layers.Dense(64, activation='relu'),
        tf.keras.layers.Dense(10, activation='softmax')
    ])
    return model

6.2 自然语言处理

def relu_in_nlp():
    """NLP中的ReLU应用"""
    model = tf.keras.Sequential([
        tf.keras.layers.Embedding(10000, 128, input_length=100),
        tf.keras.layers.Flatten(),
        tf.keras.layers.Dense(256, activation='relu'),
        tf.keras.layers.Dropout(0.5),
        tf.keras.layers.Dense(128, activation='relu'),
        tf.keras.layers.Dropout(0.5),
        tf.keras.layers.Dense(1, activation='sigmoid')  # 二分类
    ])
    return model

6.3 推荐系统

def relu_in_recommendation():
    """推荐系统中的ReLU应用"""
    # 用户特征输入
    user_input = tf.keras.layers.Input(shape=(100,))
    user_features = tf.keras.layers.Dense(64, activation='relu')(user_input)
    
    # 物品特征输入
    item_input = tf.keras.layers.Input(shape=(50,))
    item_features = tf.keras.layers.Dense(64, activation='relu')(item_input)
    
    # 特征交互
    concatenated = tf.keras.layers.concatenate([user_features, item_features])
    hidden = tf.keras.layers.Dense(128, activation='relu')(concatenated)
    hidden = tf.keras.layers.Dense(64, activation='relu')(hidden)
    
    # 输出评分
    rating = tf.keras.layers.Dense(1, activation='linear')(hidden)
    
    model = tf.keras.Model(inputs=[user_input, item_input], outputs=rating)
    return model

7. 实践建议与最佳实践

7.1 何时使用ReLU？

  • 默认选择：大多数前馈神经网络的隐藏层

  • CNN：卷积层之后的标准选择

  • 深度网络：缓解梯度消失问题

7.2 何时避免ReLU？

  • RNN：可能导致梯度爆炸

  • 输出层：根据任务选择适当的激活函数

  • 对死亡神经元敏感的任务：考虑使用Leaky ReLU变种

7.3 超参数调优建议

def relu_hyperparameter_tuning():
    """ReLU超参数调优示例"""
    
    # 学习率与ReLU的配合
    learning_rates = [0.1, 0.01, 0.001, 0.0001]
    
    # 权重初始化策略
    initializers = [
        'he_normal',  # ReLU专用初始化
        'he_uniform',
        'glorot_normal',
        'random_normal'
    ]
    
    # 批量归一化与ReLU的配合
    def create_model_with_bn(use_batch_norm=True, learning_rate=0.001):
        model = tf.keras.Sequential([
            tf.keras.layers.Dense(128, input_shape=(784,), 
                                kernel_initializer='he_normal'),
            tf.keras.layers.BatchNormalization() if use_batch_norm else tf.keras.layers.Lambda(lambda x: x),
            tf.keras.layers.ReLU(),
            tf.keras.layers.Dense(64, kernel_initializer='he_normal'),
            tf.keras.layers.BatchNormalization() if use_batch_norm else tf.keras.layers.Lambda(lambda x: x),
            tf.keras.layers.ReLU(),
            tf.keras.layers.Dense(10, activation='softmax')
        ])
        
        model.compile(
            optimizer=tf.keras.optimizers.Adam(learning_rate=learning_rate),
            loss='sparse_categorical_crossentropy',
            metrics=['accuracy']
        )
        return model
    
    return create_model_with_bn

总结

ReLU激活函数因其简单性、高效性和有效性，已经成为深度学习中最常用的激活函数之一。通过理解其数学原理、优势局限性和各种变种，我们可以在实际项目中更好地应用这一重要工具。

关键要点总结：

  1. 原理简单：f(x) = max(0, x)，计算高效

  2. 解决梯度消失：正区间导数为1，支持深层网络训练

  3. 稀疏激活：负半轴输出为0，增强模型泛化能力

  4. 注意死亡ReLU：合理设置学习率和初始化策略

  5. 灵活使用变种：根据任务需求选择合适的ReLU变体

ReLU的成功启发了更多优秀的激活函数设计，深刻影响了深度学习的发展方向。掌握ReLU及其变种，是构建高效神经网络的重要基础。

limenga102
关注
神经网络基础部件-激活函数详解
专注计算机视觉算法训练，算法优化部署以及SDK开发的知识分享。
01-10 812
本文分析了激活函数对于神经网络的必要性，同时讲解了几种常见的激活函数的原理，并给出相关公式、代码和示例图。从机器学习的角度来看，神经网络其实就是一个非线性模型，其基本组成单元为具有非线性激活函数的神经元，通过大量神经元之间的连接，使得多层神经网络成为一种高度非线性的模型。神经元之间的连接权重就是需要学习的参数，其可以在机器学习的框架下通过梯度下降方法来进行学习。
激活函数、Sigmoid激活函数、tanh激活函数、ReLU激活函数、Leaky ReLU激活函数、Parametric ReLU激活函数详细介绍及其原理详解
IronmanJay
01-05 9781
本文总结了关于激活函数、Sigmoid激活函数、tanh激活函数、ReLU激活函数、Leaky ReLU激活函数、Parametric ReLU激活函数的相关内容，详细介绍了其原理以及优缺点，本文的全部内容如下所示。
【PyTorch】PyTorch中的非线性激活函数详解：原理、优缺点与实战指南
loinleeai的博客
04-17 1375
ReLU族仍是隐藏层的首选，平衡速度与性能。GELU/Swish在复杂任务中表现优异，但需权衡计算成本。SELU在极深网络中潜力大，但依赖严格初始化。轻量型函数（如Hardswish）是移动端部署的关键。实际应用中，建议通过实验（如交叉验证）选择最佳激活函数，并结合模型结构、数据分布和硬件条件综合优化。
PyTorch 激活函数详解：从原理到最佳实践
敲代码别忘了喝上一杯凉白开。
12-20 1344
激活函数是神经网络中的核心组件，通过引入非线性特性使网络能够学习复杂的关系。本篇文章详细介绍了常见激活函数的数学原理、优缺点及其在实际应用中的选择策略。文章涵盖了 Sigmoid、Tanh、ReLU、Leaky ReLU、Softmax 和 Swish 等激活函数，分别对其输出范围、特点以及适用场景进行了对比分析，并提供了数学表达式和函数图像。此外，文章探讨了激活函数在不同任务中的具体应用，如分类、回归及深度学习模型中隐藏层的激活函数选择。
深入浅出TensorFlow激活函数实战：ReLU/Sigmoid/Softmax选择指南与完整代码实现
理论都是虚的，代码才是王道。
04-15 1123
作为神经网络的核心组件，激活函数直接决定了模型的非线性表达能力。在TensorFlow开发中，选择不当的激活函数可能导致梯度消失、训练速度缓慢等问题。举个生活化的例子：激活函数就像给咖啡加糖的过程，没有糖（激活函数）的咖啡（线性模型）虽然能解渴，但缺乏丰富的层次感。
【激活函数总结】Pytorch中的激活函数详解： ReLU、Leaky ReLU、Sigmoid、Tanh 以及 Softmax
阿旭的博客
09-07 2130
【激活函数总结】Pytorch中的激活函数详解： ReLU、Leaky ReLU、Sigmoid、Tanh 以及 Softmax
深度神经网络详解：原理、架构与应用
yuanxifan的博客
06-19 3425
深度神经网络作为现代机器学习的核心技术，已经在多个领域展示了其强大的能力。本文从基本原理、常见架构、实际应用和案例分析等方面，详细解析了深度神经网络的各种技术细节。通过合理利用深度神经网络，我们可以解决许多复杂的实际问题，推动技术进步和应用创新。希望本文能为你提供一个全面的深度神经网络入门指南，助力你的学习和研究。
卷积神经网络(CNN)详解：原理、核心组件与应用实践
嗨，欢迎来到我的 CSDN 博客小天地！一名深耕多年的技术发烧友。在这里，我将把日常工作中积累的宝贵经验，从复杂架构设计的精妙之处，到代码优化的实战技巧，毫无保留地分享给大家。
04-27 1643
卷积神经网络(CNN)详解：原理、核心组件与应用实践
transformer详解：原理和应用
A1233242的博客
06-28 1963
Transformer 模型是一种基于注意力机制的深度学习模型，Transformer 彻底改变了自然语言处理（NLP）领域，并逐渐扩展到计算机视觉（CV）等领域。Transformer 的核心思想是完全摒弃传统的循环神经网络（RNN）结构，仅依赖注意力机制来处理序列数据，从而实现更高的并行性和更快的训练速度。
激活函数详解：深度学习的基础与应用
每种激活函数都有其适用的场景和问题，因此在实际应用中，通常需要根据具体任务和网络结构去选择合适的激活函数。 对于初学者而言，理解激活函数的工作原理后，应该通过实验来掌握如何选择和调整激活函数。例如，...
人工智能基于神经网络的Matlab建模与应用：原理详解及代码实战
09-09
内容概要：本文系统介绍了神经网络的基本原理及其在Matlab中的实现方法，涵盖神经网络的起源与发展、核心结构（输入层、隐藏层、输出层）、神经元工作机制、激活函数（如Sigmoid、ReLU、Tanh）、前向传播与反向传播...
【激活函数与损失函数】：TensorFlow实现与应用详解
[【激活函数与损失函数】：TensorFlow实现与应用详解](https://img-blog.csdnimg.cn/20190106103701196.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0...
工业互联网中的AI与大数据：推动智能化决策的力量
最新发布
2509_93699011的博客
11-16 452
摘要： 工业互联网通过融合大数据、人工智能（AI）和物联网（IoT）技术，推动制造业智能化升级。大数据实时采集生产设备、质量及供应链数据，优化生产调度与能源管理；AI则通过机器学习实现预测性维护、智能决策和质量检测。二者协同驱动实时分析与自适应优化，应用于智能工厂、供应链及物流管理。未来，边缘计算和数据安全将成为发展重点，AI自学习能力将进一步提升自动化水平，助力制造业高效转型。
参赛项目实战：校园智能助手 Agent 开发全记录，从 0 到 1 打造高效校园生活解决方案
yzx991013的博客
11-16 408
《校园全能助手智能体开发全记录》摘要：本文详细介绍了基于ChatGLM-6B开发的校园智能助手项目，旨在通过AI技术解决学生校园生活中的痛点需求。该项目整合课程查询、学习辅助、生活服务等模块，采用LangChain框架实现自然语言交互和任务自动调度。开发过程中攻克了多模块协同、数据接口对接等难题，最终实现1.5秒快速响应和88%复杂任务执行成功率。测试阶段覆盖1000+学生，满意度达85分。项目具有场景适配性强、轻量化部署等优势，未来计划扩展多模态交互和跨校适配功能，打造更智能的校园服务体系。
人脸检测识别技术
m0_49367516的博客
11-13 1273
人脸识别
1.3 半监督学习黑科技：如何用少量标注数据提升模型性能，节省90%标注成本？
yonggeit的博客
11-12 1324
半监督学习：用少量标注数据提升模型性能 半监督学习是一种混合监督和无监督学习的方法，通过同时利用少量标注数据和大量未标注数据来训练模型，可显著降低标注成本。核心思想包括： 自训练：模型为高置信度未标注数据生成伪标签，迭代扩充训练集 协同训练：利用不同特征视图训练多个模型互相提供伪标签 一致性正则化：对数据增强样本强制输出一致性 实验表明，仅使用10%标注数据配合半监督学习，就能达到接近全监督学习的性能。这种方法特别适用于标注成本高的医疗影像、自然语言处理等领域，可节省90%以上标注成本。
物联网设备运维中的自适应数据流处理与动态资源分配优化
etower的博客
11-14 576
物联网运维正在经历从"数据搬运工"到"智能决策中枢"的范式革命。通过自适应数据流处理与动态资源分配的深度耦合，我们正在构建一个万物智联、能量自洽的生态系统。当边缘计算的算力触角延伸至每个传感器节点，当AI算法在毫秒级时延内完成决策闭环，我们将见证真正意义上的数字文明崛起。
【DINOv3】（5）例程 2：特征提取与图像匹配例程
youcans的博客
11-16 839
DINOv3模型在图像特征提取与匹配任务中表现出色。本文基于DINOv3官方例程dense_sparse_matching.ipynb，改写为本地可运行的Python程序，实现两种特征匹配方式：(1)密集匹配：生成全图匹配热力图，验证特征语义一致性；(2)稀疏匹配：精确定位关键patch对应关系。程序包含完整流程：环境配置、模型加载、图像预处理、特征提取、相似度计算和可视化。通过PCA降维和高维特征匹配，展示DINOv3在跨视角、光照变化下的鲁棒性。
Product Hunt 每日热榜 | 2025-11-12
LaughingZhu的博客
11-12 2174
Product Hunt 每日热榜 | 2025-11-12 Talo 提供实时语音翻译，适用于视频通话、现场活动、离线演示和播放直播等场景。你可以使用机器人或桌面应用来翻译会议，也可以通过我们的 API 进行集成。让每一次对话都能在全球范围内无障碍交流。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值