469. Convex Polygon

469. Convex Polygon

Given a list of points that form a polygon when joined sequentially, find if this polygon is convex (Convex polygon definition).

Note:

1. There are at least 3 and at most 10,000 points.
2. Coordinates are in the range -10,000 to 10,000.
3. You may assume the polygon formed by given points is always a simple polygon (Simple polygon definition). In other words, we ensure that exactly two edges intersect at each vertex, and that edges otherwise don't intersect each other。

1. Example 1:

2. [[0,0],[0,1],[1,1],[1,0]]
   
   Answer: True
   
   Explanation:
   

   Example 2:

   [[0,0],[0,10],[10,10],[10,0],[5,5]]
   
   Answer: False
   
   Explanation:

分析：

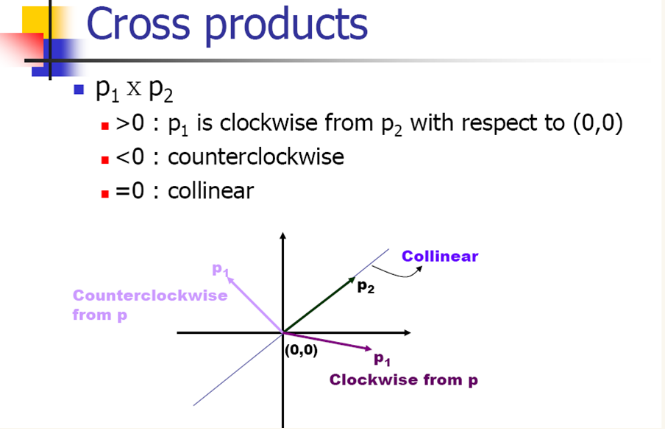
只需按逆时针一次判断一边和一点的关系，若叉积>0，则表示存在大于180的内角，即为凹多边形。

对于任意两点组成的直线，第3点相对于这条直线都有3种关系，在线上，在线的左边，在线的右边。如果一个多边形是凸的，则对于多边形的任意一条边，其他的n-2个点必定都在边的同一侧。

假设有两点A(a[0],a[1])，B(b[0],b[1])，则直线AB的表示：(y-a[1])/(x-a[0])=(b[1]-a[1])/(b[0]-a[0])。对于任意点C(c[0],c[1]),要判断点C相对于直线AB的关系，将x=c[0]带入，y=(b[1]-a[1])/(b[0]-a[0])*(c[0]-a[0])+a[1]；则y-c[1]=(b[1]-a[1])/(b[0]-a[0])*(c[0]-a[0])+a[1]-c[1]；化简，判断符号。如果为正，说明，点C在直线AB的上边，为负在直线的下边，=0表示在直线上。

class Solution {
    int judge_side(vector<int>& a,vector<int> & b,vector<int> & c)//判断点与线的相对位置
    {
        int ans = (a[1]-b[1])*c[0]-c[1]*(a[0]-b[0])+a[0]*b[1]-a[1]*b[0];
        return ans==0?0:ans<0?-1:1;
    }
public:
    bool isConvex(vector<vector<int>>& points) {
      int n=points.size(); 
      int i;
      int turn=0,next=0;
      for(i=0;i<n;i++)
      {
          next=judge_side(points[i],points[(i+1)%n],points[(i+2)%n]);
          if(turn&&next&&next!=turn) return 0;
          turn=next;
      }
      return 1;
    }
};

更新:因为增加了新的测试用例:针对上一次的角度恰好是180度的情形.

class Solution {  
    int judge_side(vector<int>& a,vector<int> & b,vector<int> & c)//判断点与线的相对位置  
    {  
        int ans = (a[1]-b[1])*c[0]-c[1]*(a[0]-b[0])+a[0]*b[1]-a[1]*b[0];  
        return ans==0?0:ans<0?-1:1;  
    }  
public:  
    bool isConvex(vector<vector<int>>& points) {  
      int n=points.size();   
      int i,j;  
      int turn=0,next=0;  
      for(i=0;i<n;i++)  
      { 
          next=judge_side(points[i],points[(i+1)%n],points[(i+2)%n]);  
          if(next)
          {
              if(turn*next<0) return 0;
              turn=next;
          }
      }  
      return 1;  
    }  
};  

 for example [[0,0],[0,1],[1,1],[2,1],[2,2],[2,3],[3,3],[3,0]]: