RFID数据完整传输

在读写器与电子标签的无线通信中，存在许多干扰因素，最主要的干扰因素是信道噪声和多卡操作。在RFID系统中，为防止各种干扰和电子标签之间数据的碰撞，经常采用差错控制和防碰撞算法来分别解决这两个问题。

1）标签冲突：   

         a. 随机性解决方案  一般采用ALOHA算法；
         b. 确定性解决方案  一般采用树型搜索算法。
 
2）读写器冲突：

         a. 多个读写器在相同频段上运行引起的频率干扰；  
         b. 多个相邻的读写器试图与一个标签进行通信而引起的标签干扰。
         解决的方法：对相邻的读写器分配在不同的频率或时隙。
 

         差错控制是一种保证接收数据完整、准确的方法。在数字通信中，差错控制利用编码方法对传输中产生的差错进行控制，以提高数字消息传输的准确性。

1. 差错的分类
    （1）随机错误
    （2）突发错误
2. 差错的衡量指标
    误码率（Bit Error Ratio，BER）是衡量在规定时间内数据传输精确性的指标。

3.差错控制的基本方式
    差错控制编码可以分为检错码和纠错码。检错码能自动发现差错的编码； 纠错码不仅能发现差错，而且能自动纠正差错的编码。
    （1）反馈纠错（ARQ）
    （2）前向纠错（FEC）
    （3）混合纠错
（1） 信息码元与监督码元
    信息码元又称为信息序列或信息位，这是发端由信源编码得到的被传送的信息数据比特，通常以k表示。监督码元又称为监督位或附加数据比特，这是为了检纠错码而在信道编码时加入的判断数据位，监督码元通常以 r 表示。


（2）许用码组与禁用码组
（3）编码的效率
    编码效率越高，信道中用来传送信息码元的有效利用率就越高。编码效率的计算公式为


    （4）码重与码距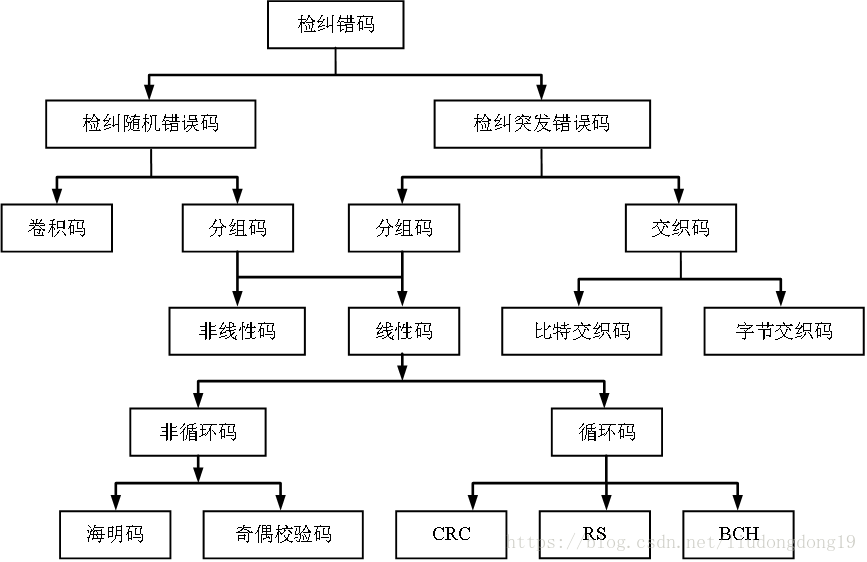

例题：

多路存取法

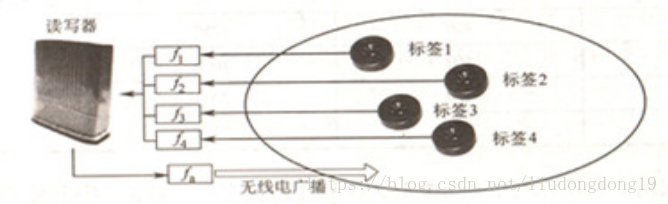
   “无线广播”式
           从读写器到多个电子标签的工作方式，读写器发送的信号同时被多个标签接收。
多路存取通信
              读写器的工作范围同时有多个电子标签，多个电子标签同时将数据传送给读写器

 

方法：

空分多路法（Space Division Multiple  Access，SDMA）

频分多路法（Frequency Division Multiple Access，FDMA）

时分多路法（Time Division Multiple Access，FDMA）
码分多路法（Code Division Multiple Access，CDMA）

防碰撞算法：

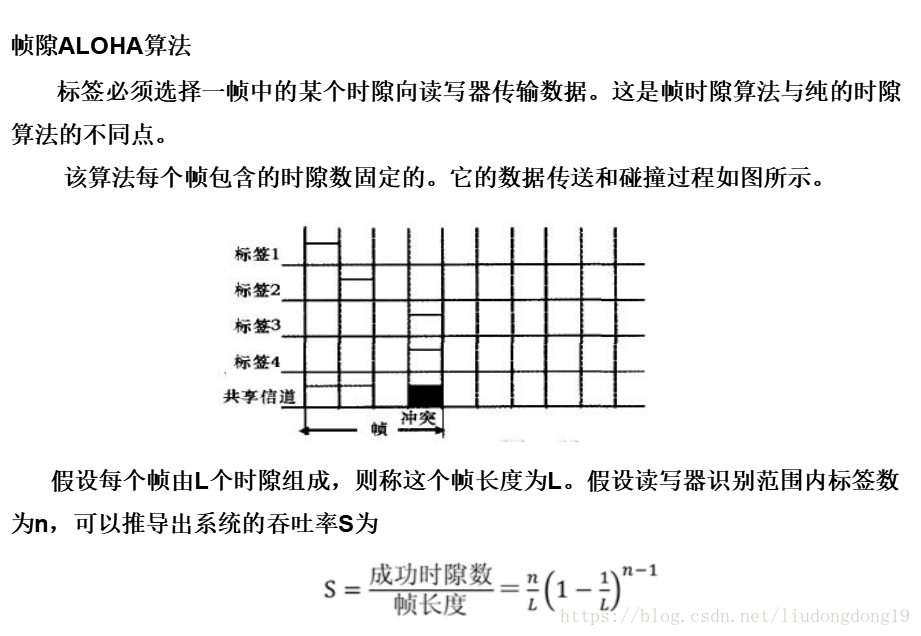
通道的平均吞吐率S为     

2）时隙ALOHA算法

      它是将信道分成许多时隙 (slot) ，每个时隙正好传送一个分组。时隙的长度由系统时钟决定，各控制单元必须与此时钟同步
     算法过程主要通过3个命令实现：
      （1）REQUEST(请求），使读写器作用范围内的所有标签同步，并促使标签在下一个时隙里将它的序列号传输给读写器；
      （2）SELECT（选择序列号），将一个事先确定的序列号作为参数发送给标签；
      （3）READ-DATA（读出数据），被选中的标签对此命令进行响应。

动态时隙ALOHA算法：

帧长度调整方法有两种：
           a. 根据前一帧通信攻取到的空闲时隙数、碰撞时隙数和成功时隙数来估计标签的数量，由估计量来调整下一帧的长度；
           b. 用REQUEST命令传送可供标签使用的时隙数时，如果有较多的标签在两个发生碰撞，就用下一个REQUEST命令增加可供使用的时隙数量（如2、4、8、16、32……），直至能够发现一个唯一的标签为止。