牛顿迭代法

1. #include <iostream.h>
2. #include <math.h>
3. #define Precision 0.000001      //控制精度要求
4. #define MaxIterative 60         //最大允许迭代次数
5. void function(double &x,double &y0,double &y1)
6. {
7.     y0=x*x*x-3*x-1.0;//原函数
8.     y1=3.0*x*x-3;  //函数导数
9. }
10. double NewtonIterative (double &x,void f(double &x,double &y0,double &y1))
11. {
12.     int MI;
13.     double y0,y1,PCS,x0,x1,PCSy;//MI均来计算迭代的次数，PCS表示x0与x1的差，PCSy表示x1对应的y的绝对值
14.     MI=MaxIterative;
15.     x0=x;
16.     f(x0,y0,y1);    //先运行一次，计算出y0,y1
17.     PCS=Precision+1.0;
18.     while ((PCS>=Precision)&&(MI!=0))//结束迭代过程的条件,x,y
19.     {
20.         if (fabs(y1+1.0==1.0))//判断导数是否为0
21.         {
22.             
23.             cout<<"wrong";
24.             return -1;
25.         }
26.             
27.         x1=x0-y0/y1;  //迭代计算x1=x0-f(x0)/f'(x0);
28.         f(x1,y0,y1);
29.         PCS=fabs(x1-x0);
30.         PCSy=fabs(y0);
31.         if(PCSy>PCS)
32.             PCS=PCSy;
33.         x0=x1;
34.         MI=MI-1;
35.     }
36.     x=x1;               //把最后求出的结果付给x
37.     return MaxIterative-MI;//迭代的次数
38. }
40. main()
41. {
42.     int k;
43.     double x;
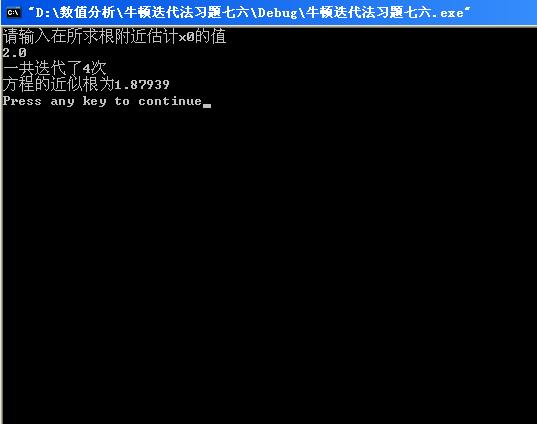
44.     cout<<"请输入在所求根附近估计x0的值"<<endl;
45.     cin>>x;
46.     k=NewtonIterative (x,function);
47.     if (k>=0)
48.     {
49.         cout<<"一共迭代了"<<k<<"次"<<endl;
50.         cout<<"方程的近似根为"<<x<<endl;
51.     }
52.     return 0;
53. }

牛顿迭代法