关于一元方程求根中牛顿迭代法的分析

观止study

已于 2024-06-13 10:13:28 修改

阅读量759

点赞数 11

分类专栏：项目开发文章标签：算法 python 牛顿迭代法

于 2024-06-13 09:24:28 首次发布

本文链接：https://blog.csdn.net/m0_66570338/article/details/139641690

版权

项目开发专栏收录该内容

5 篇文章 18 订阅

订阅专栏

文末含有程序源代码以及可执行exe文件，文中部分内容参考网上博客以及GPT协助，希望能对你有所帮助~

一、理论知识简述

牛顿迭代法（Newton’s Method），也称为牛顿-拉弗森方法（Newton-Raphson Method），是一种用于寻找函数零点或者说方程的根的迭代数值方法。它是一种非常有效的数值分析技术，具有收敛速度快的特点，通常用于求解实数域上的非线性方程，特别是在科学和工程领域中经常遇到的问题。

牛顿迭代法的基本思想是通过不断地逼近函数零点来求解方程。其迭代过程如下：

初始值选择：选择一个初始猜测值 ( x₀ ) 作为函数的根的近似值。
迭代公式：根据函数的导数和当前的猜测值，使用牛顿迭代公式进行迭代计算： $x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$
迭代更新：重复步骤2，实际中 $x_{n+1}=x_n$ 可能永远达不到，可根据给定的条件进行判断，迭代到满足停止迭代的条件，如达到指定的精度要求 $x_{n+1}-x_n|<△$ 或达到最大迭代次数，此时的 $x_{n+1}$ 即为所求。

迭代公式简单推导：

假设 f(x) 是关于x的函数，求出 f(x) 的一阶导，即斜率：

$f'(x_n) = \frac{△y}{△x} = \frac{f(x_n) - 0}{x_n - x_{n+1}} = \frac{0 - f(x_n)}{(x_{n+1}-x_n)}$

简化等式即可得到迭代公式：

$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$

然后便可以利用得到的最终式进行迭代运算直到求到一个比较精确的值
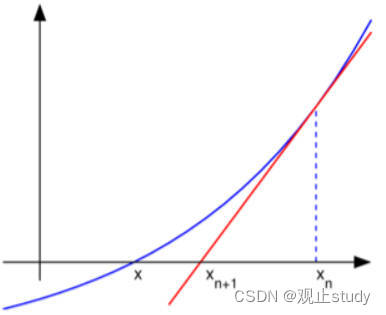
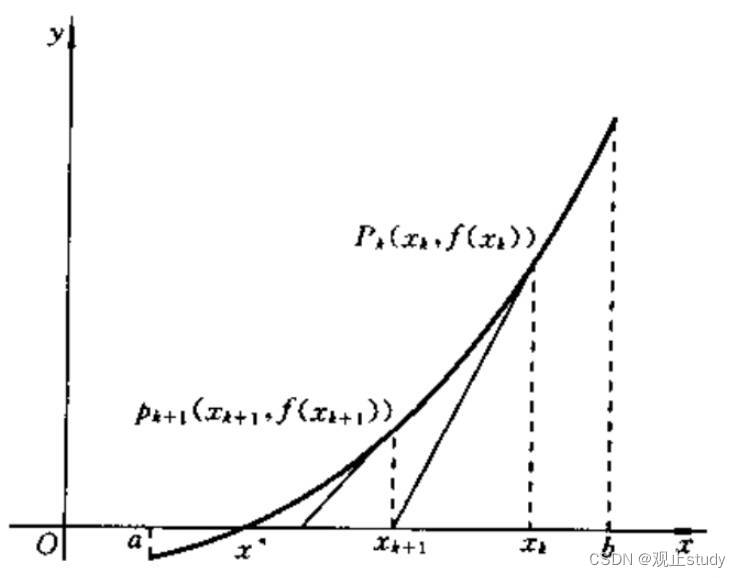
在这里插入图片描述

Newton迭代法的几何解释：

方程 f(x) = 0 的根 $x^*$ 为 y = f(x) 和 y = 0 (即x轴)的交点，设 $x_k$ 为 $x^*$ 的某个初始近似值，过 $P_k$ 点 ( $x_k$ , $f(x_k)$ ) 作 y = f(x) 的切线交 x 轴于 $x_{k+1}$ ，即为所求得的近似值。继续过 $P_{k+1}$ 点 ( $x_{k+1}$ ， $f(x_{k+1})$ ) , $P_{k+2}$ 点 ( $x_{k+2}$ ， $f(x_{k+2})$ )，···，作 y = f(x) 的切线，即可逐步逼近精确的根 $x^*$ 。因此，Newton法也叫切线法，因为它是沿着曲线 y = f (x) 上某一点作切线逐步外推逼近的。从 $P_K$ 点作切线与x轴的交点 $x_{k+1}$ ，由于 y = f(x) 不是直线，所以 $f (x_{k+1})$ 就不可能为零。因此必须以 $x_{k+1}$ 作为新的起点，从与之对应的 $P_{k+1}$ 点继续作切线，重复上述步骤，直至 $f(x_{k+1})$ 充分小，逼近零时为止。
在这里插入图片描述

牛顿迭代法具有如下特点：

收敛性：在满足一定条件下，牛顿迭代法通常具有二阶收敛性，即每次迭代后，误差的平方将减小为原来的四分之一。
初值敏感性：牛顿迭代法对初始猜测值 ( x₀ ) 的选择十分敏感，不同的初始值可能会导致不同的迭代结果，甚至可能出现发散的情况。
局部收敛：牛顿迭代法只能保证在初始猜测值附近的某个范围内收敛到函数的一个根，如果初始猜测值距离根较远，可能导致迭代过程不收敛或收敛到错误的根。

二、实现算法介绍

牛顿迭代法核心算法实现逻辑：

from sympy import *
# 定义变量
x = Symbol('x')
# 解析输入的函数函数
self.f_expr = eval(self.function_entry.get())
# 使函数可调用
self.f = lambdify(x, self.f_expr)
# 求函数的一阶导数
self.df_expr = diff(self.f_expr, x)
# 使函数可调用
self.df = lambdify(x, self.df_expr)

# 牛顿法(输入三个参数，初始猜值、误差、最大迭代次数)
def Newton(self, x0, E, max_count=100):
    # 存放迭代过程中的所有解
    ans_list = [x0] 
    # 最大迭代次数，避免死循环
    for i in range(max_count):  
        # 迭代公式
        ans_list.append(ans_list[i] - self.f(ans_list[i]) / self.df(ans_list[i]))  
        # 判断是否满足误差要求，达到直接中止迭代
        if abs(ans_list[i + 1] - ans_list[i]) <= E:
            break
    # 返回最终迭代结果，迭代次数，迭代过程全解
    return ans_list[i + 1], i + 1, ans_list

核心代码讲解：

from sympy import * 将 SymPy 中所有的功能都导入到当前命名空间中，包括常用的数学函数、符号、表达式、方程、矩阵等。这样一来，你可以直接使用这些功能而不用再使用 sympy. 这样的前缀。
x = sp.Symbol('x')：定义一个符号变量 x，用于表示函数中的自变量。
self.f_expr = eval(self.function_entry.get())：从用户输入的字符串中解析函数表达式。假设用户在界面上输入了一个函数表达式，通过 self.function_entry.get() 获取用户输入的字符串，然后通过 eval() 函数将其解析成可执行的Python代码，将结果存储在 self.f_expr 中。
self.f = sp.lambdify(x, self.f_expr)：使用 sp.lambdify() 函数将SymPy表达式 self.f_expr 转换为一个可调用的函数 self.f。这样做是为了将SymPy的符号表达式转换为可以在数值计算中使用的函数。
self.df_expr = sp.diff(self.f_expr, x)：求解函数 self.f_expr 对变量 x 的一阶导数。sp.diff() 函数用于对表达式求导。
self.df = sp.lambdify(x, self.df_expr)：将一阶导数 self.df_expr 转换为一个可调用的函数 self.df。
def Newton(self, x0, E, max_count=100):：定义一个名为 Newton 的方法，用于执行牛顿迭代法。
ans_list = [x0]：初始化一个列表 ans_list，用于存放迭代过程中的所有解，并将初始猜测值 x0 添加到列表中。
for i in range(max_count):：使用 for 循环迭代最多 max_count 次，避免死循环。
ans_list.append(ans_list[i] - self.f(ans_list[i]) / self.df(ans_list[i]))：根据牛顿迭代法的公式更新迭代解。迭代公式即为 $x_{k+1} = x_k - \frac{f(x_k)}{f'(x_k)}$ ，其中 self.f(ans_list[i]) 表示函数在点 ans_list[i] 处的函数值，self.df(ans_list[i]) 表示函数在点 ans_list[i] 处的导数值。
if abs(ans_list[i + 1] - ans_list[i]) <= E:：判断迭代结果与上一次迭代结果之间的差值是否小于等于给定的误差 E，如果满足条件则跳出循环，迭代结束。
return ans_list[i + 1], i + 1, ans_list：返回迭代过程中最终得到的近似根 ans_list[i + 1]、迭代次数 i + 1，以及整个迭代过程中的所有解 ans_list，用作与界面渲染数据源。

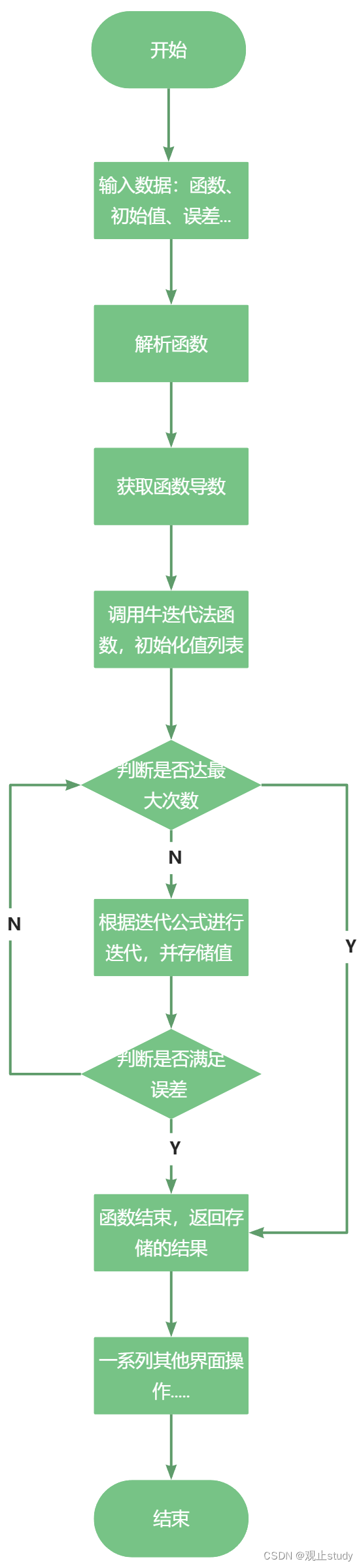
算法流程图：

在这里插入图片描述

三、作品实现展示

1）运行程序的两种方式：可以在Python环境下运行Newton.py源文件或者直接双击运行Newton.exe程序。

2）运行程序的效果如下：
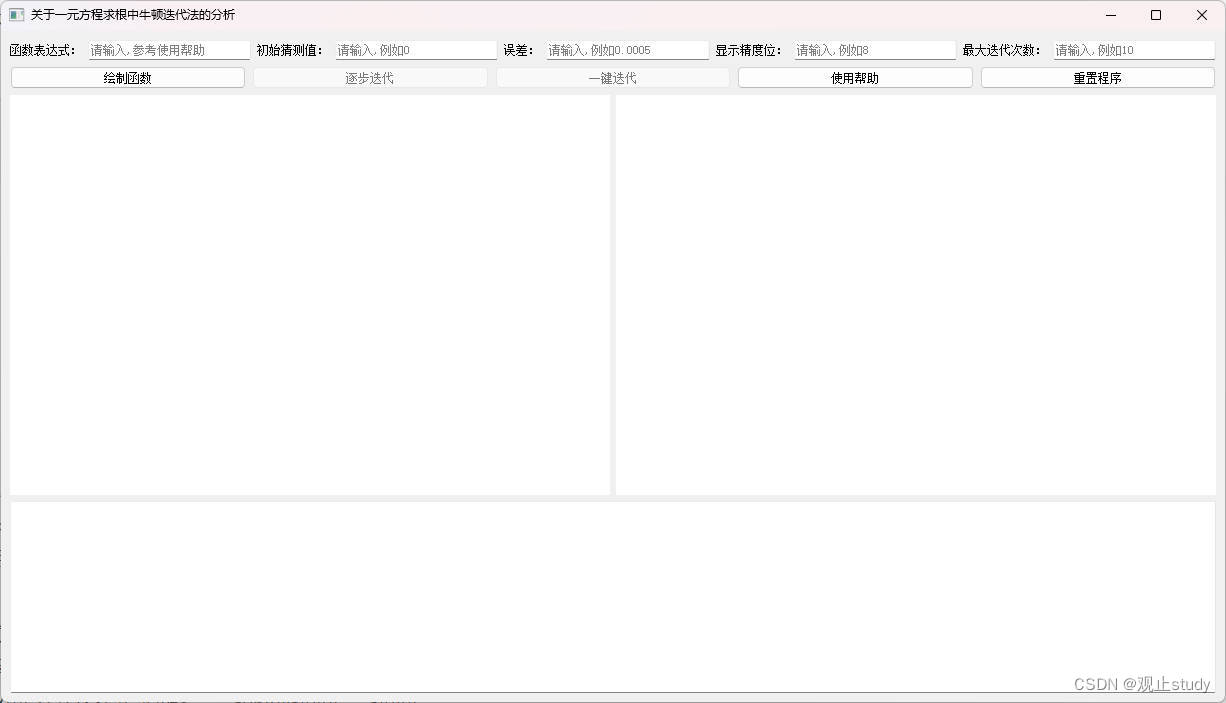
在这里插入图片描述

3）主体模块介绍：程序的第一行为相关数据输入框，第二行为相关操作按钮，第三行分别为函数图像、迭代值变化趋势图像，第四行为迭代值、迭代次数显示区。以下是每个输入框和按钮的作用以及输入函数的格式要求，可在程序中通过使用帮助查看：

函数表达式输入框：
请输入一个数学函数表达式，例如： $x * * 2 + 3 x - 5 、 s p . e x p (x) + 10 x - 2$ 。
表达式应当符合python语法，如加法(+), 减法(-), 乘法(*), 除法(/), 幂(**)。
特殊函数输入格式请参考SymPy官方文档，例如 $e^x$ => exp(x),sin(x) => sin(x)

SymPy官方文档：https://docs.sympy.org/latest/tutorials/intro-tutorial/index.html#intro-tutorial

Python语法学习：https://blog.csdn.net/m0_66570338/article/details/128714062
初始猜测值输入框：
输入一个初始猜测值，作为迭代计算的起始点。
可以输入整数或小数。
误差输入框：
输入一个用于判断迭代精度的误差值。
当迭代结果与上一次迭代结果的差值小于误差时，迭代停止。
显示精度位输入框：
设置迭代过程中结果的显示精度位数。
输入一个正整数，表示显示结果的小数位数。
最大迭代次数输入框：
设置最大迭代次数，以避免迭代无限循环。
输入一个正整数，表示最大的迭代次数。
绘制函数按钮：
根据输入的函数表达式，绘制函数图像。
逐步迭代按钮：
逐步展示迭代过程的图像，并显示每次迭代的结果。
一键迭代按钮：
一次性展示所有迭代过程的图像，并显示最终的迭代结果。
重置程序按钮：
重置所有的操作记录，清空输入框和图像区域，恢复到初始状态。

4）首先按照输入格式规范为每个输入框输入初始值：
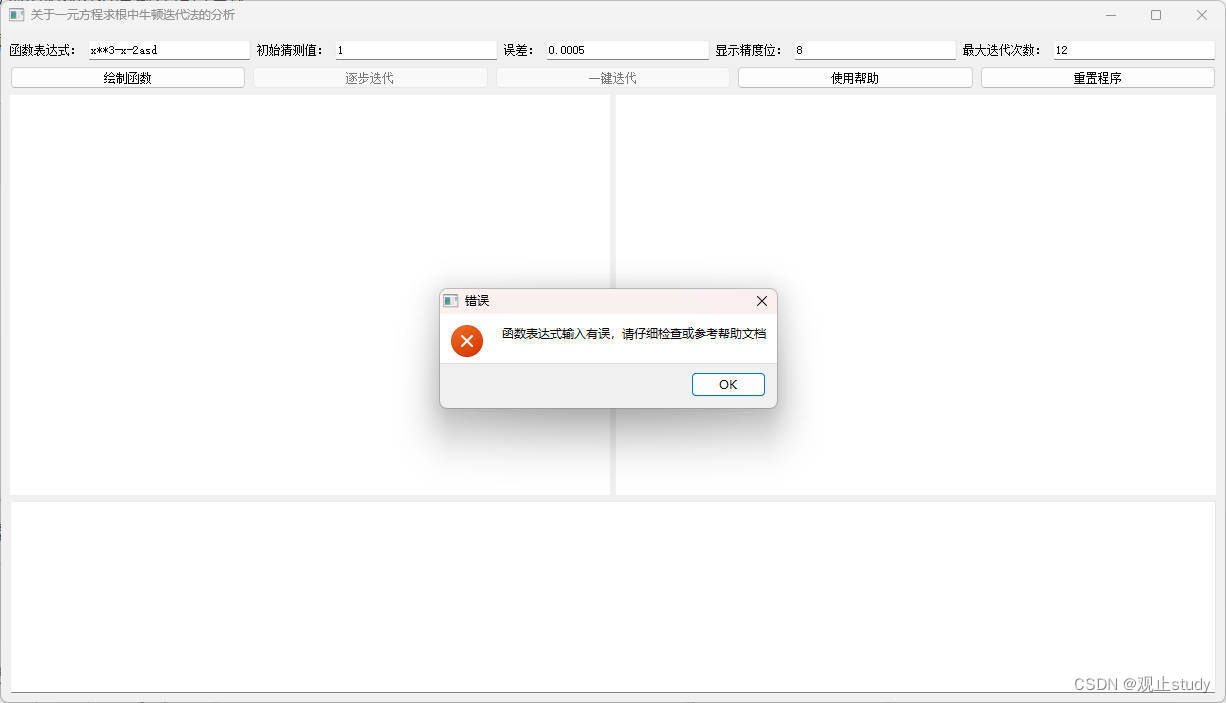
在这里插入图片描述

5）首先点击绘制函数按钮，程序将检测初始值输入是否有误：

如果输入有误程序将拦截后续操作：

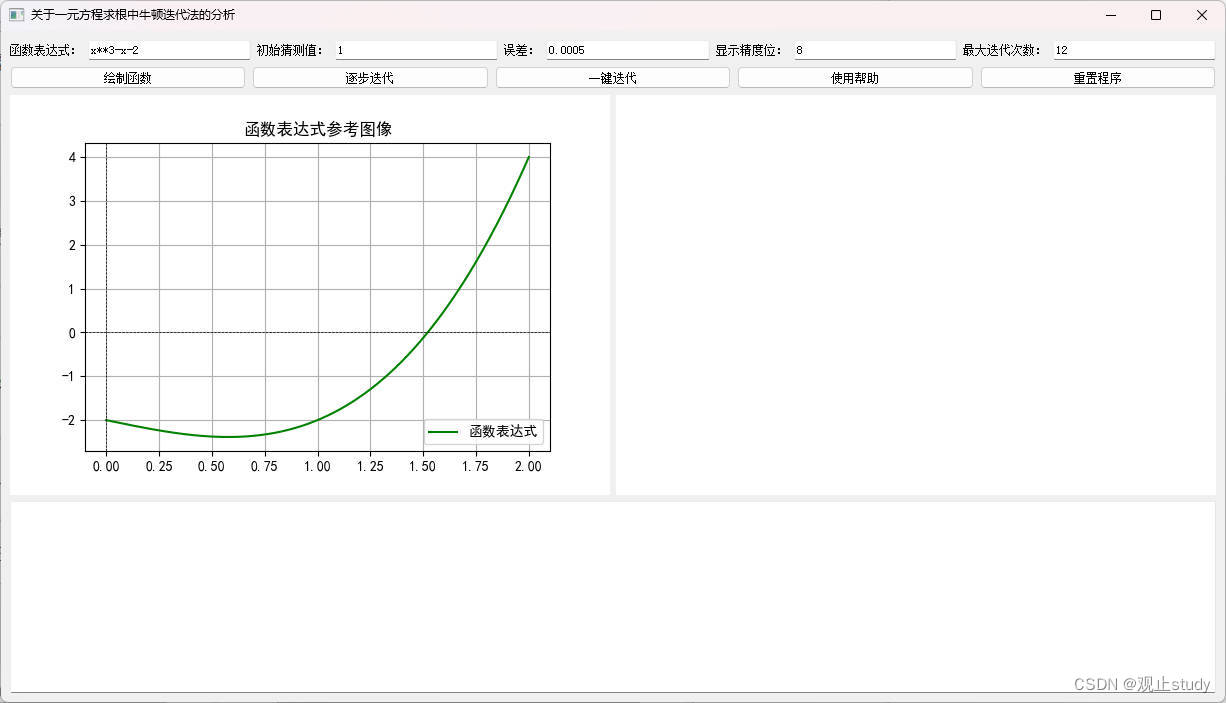
在这里插入图片描述

如果无误将绘制函数表达式图像，同时解锁逐步迭代、一键迭代操作按钮：

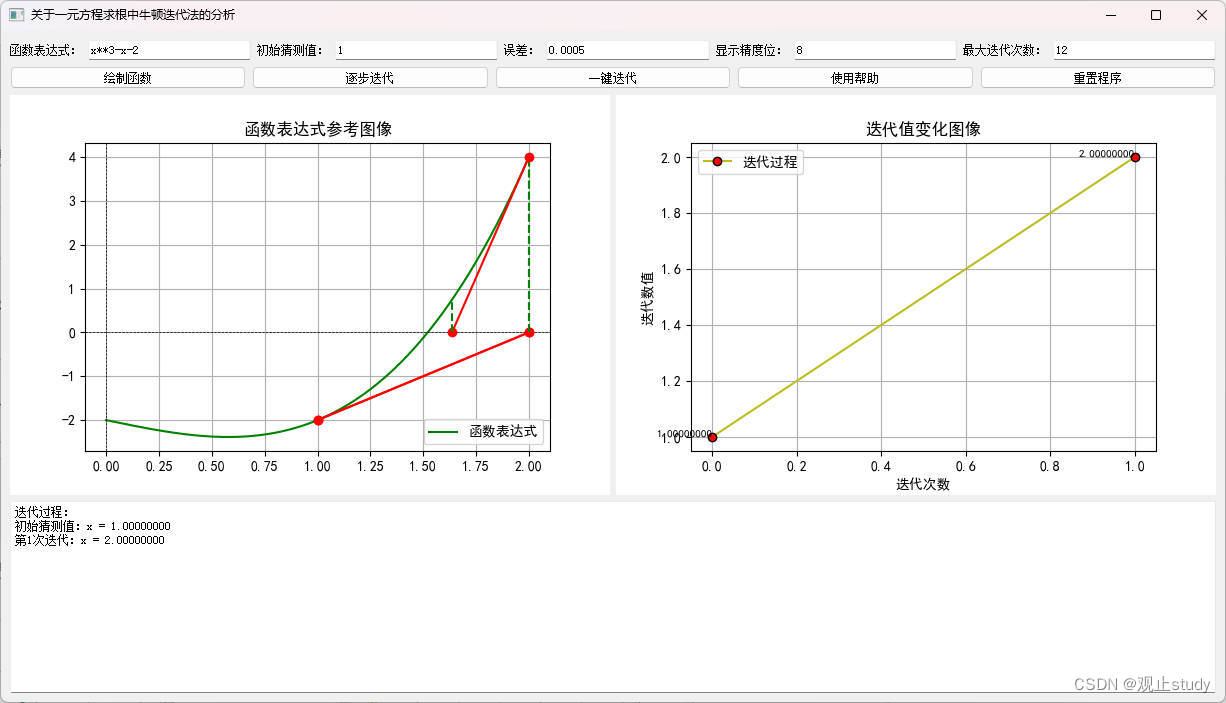
在这里插入图片描述

6）可以选择逐次点击逐步迭代按钮一步步查看迭代过程值变化情况：

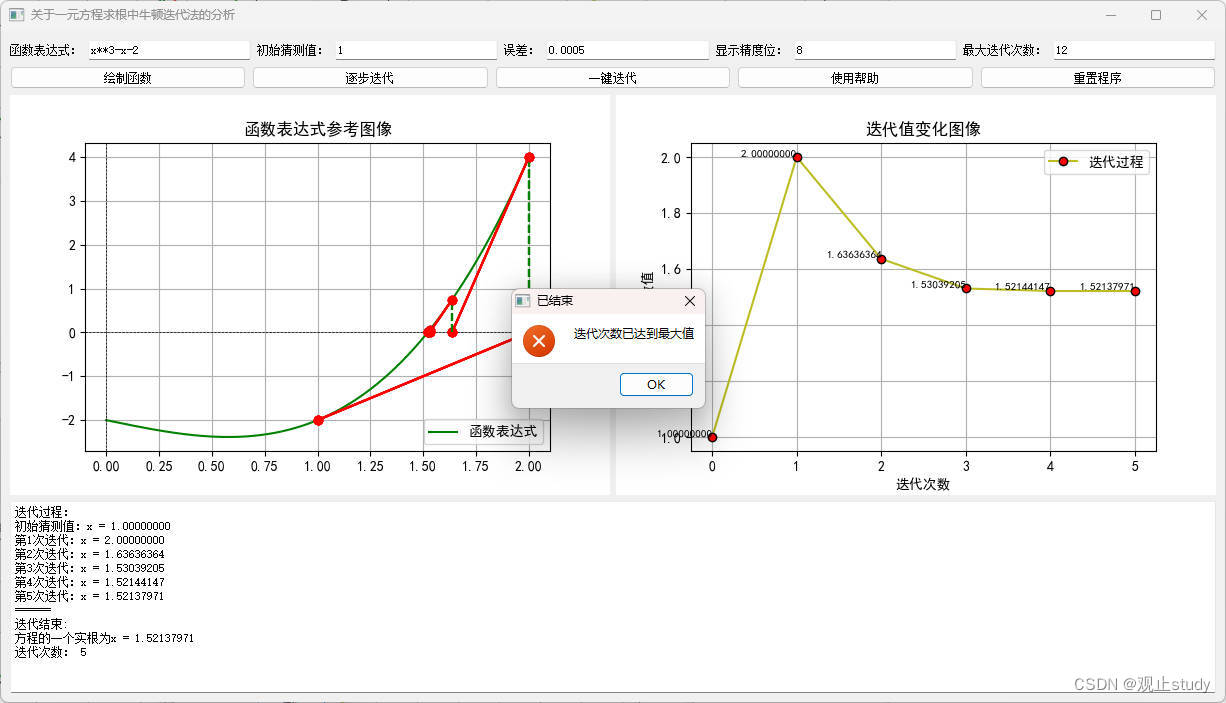
在这里插入图片描述

7）也可以点击一键迭代按钮，立即查看整个迭代过程和迭代结果：

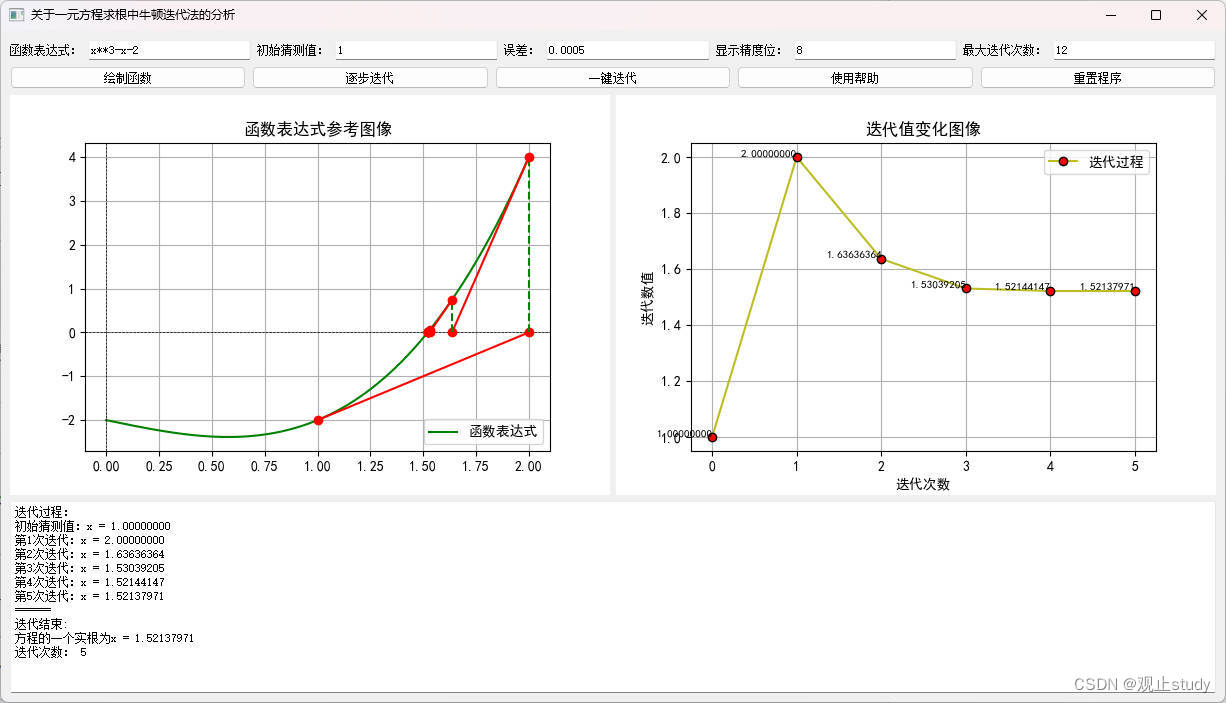
在这里插入图片描述

8）如果修改了任意输入框中的值函数图像和迭代结果都将清空，需要重新绘制函数，这是为了重复检查输入值正确性。

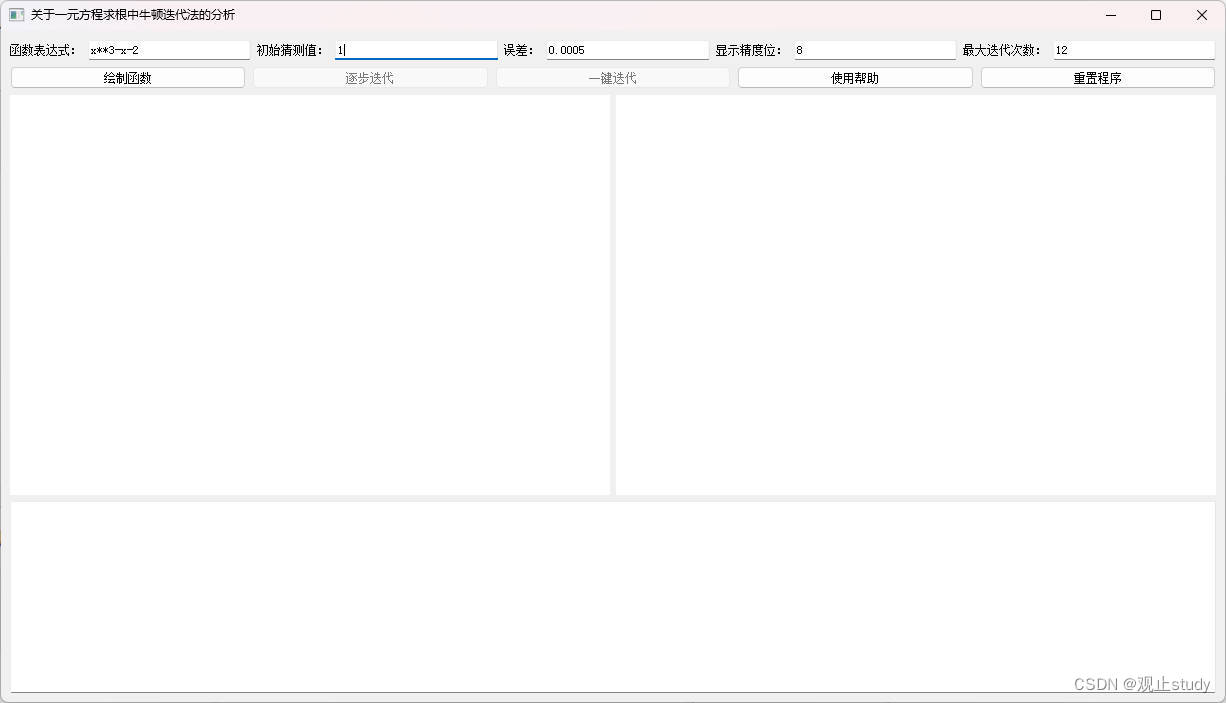
在这里插入图片描述

9）可以点击重置按钮，将清空所有值

在这里插入图片描述

10）可以点击使用帮助，可借此查看程序相关使用说明：

在这里插入图片描述

11）使用小技巧：由于迭代点、切线变化可能会比较散乱或者比较密集不便于查看，由此可以尝试长按鼠标拖动查看图像或者通过滚轮放大或缩小图像查看效果。

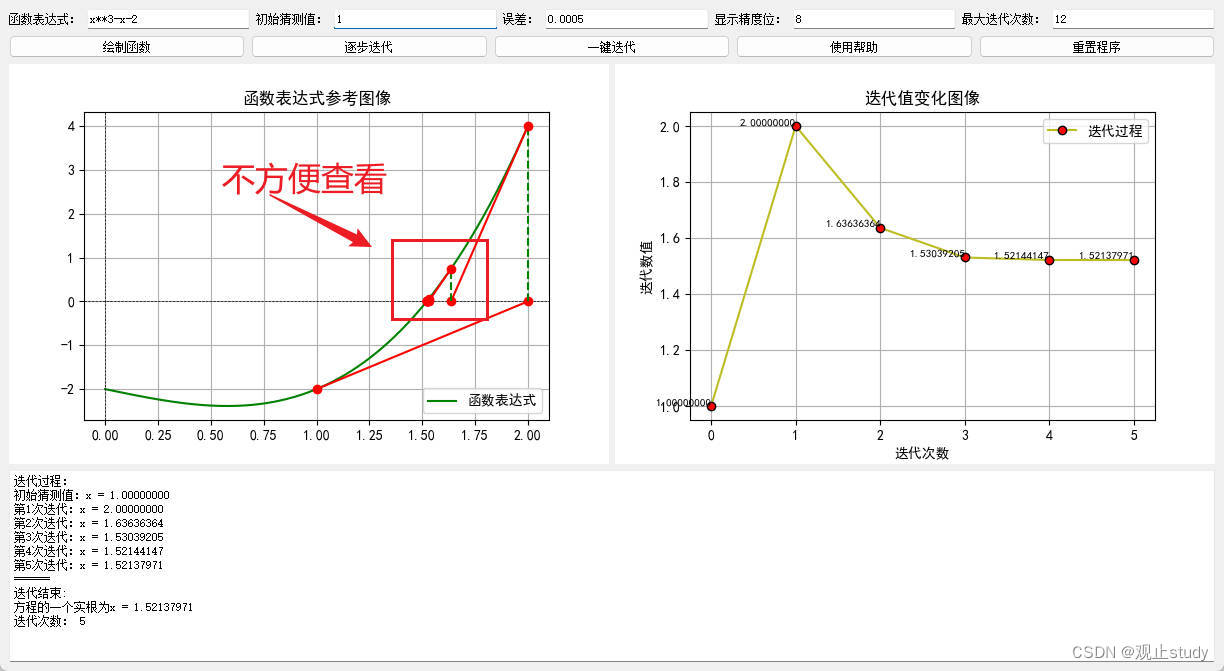
在这里插入图片描述

通过滚轮放大后查看效果：

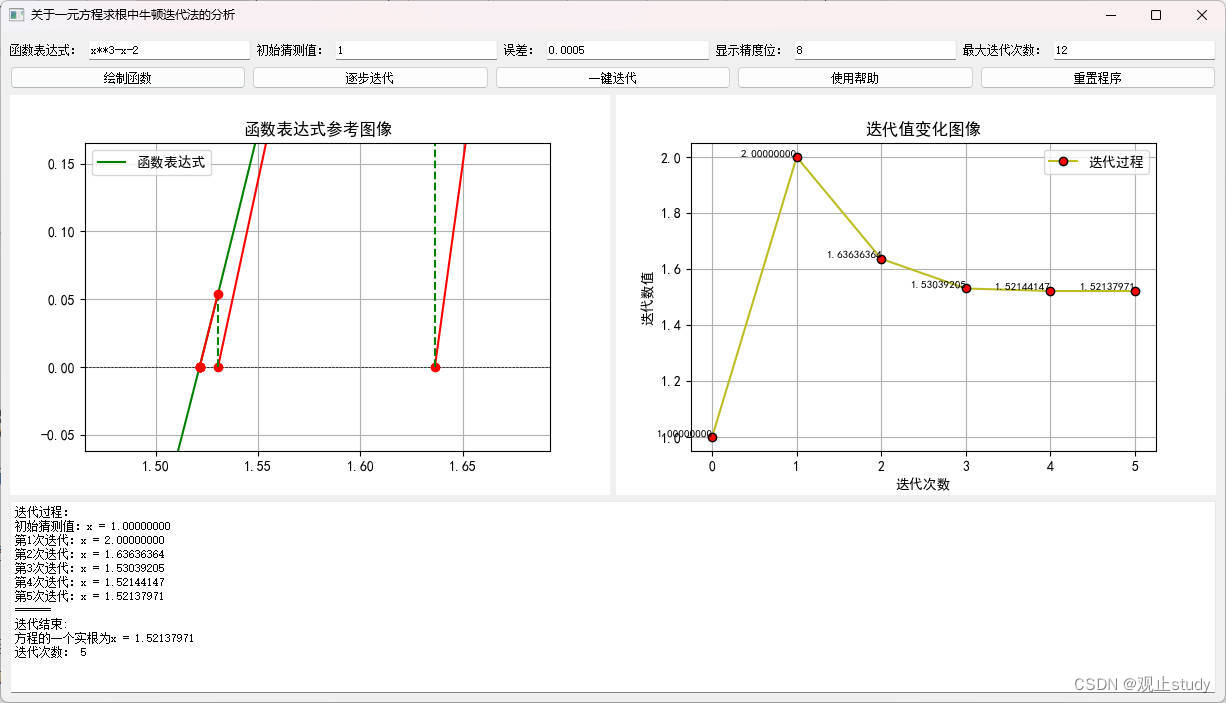
在这里插入图片描述

如此用起来便方便很多~

四、知识应用讨论

牛顿迭代法及其类似思路在实际工程问题中有着广泛的应用，特别是在需要解决非线性方程、优化问题或者求解数值逼近的情况下。以下是一些典型的应用领域：

电力系统分析：在电力系统工程中，牛顿迭代法被广泛应用于潮流计算。电力系统是一个复杂的网络，包含各种各样的电力设备，如发电机、变压器、线路等。潮流计算是电力系统分析中的核心问题之一，其主要目的是计算电力系统中各节点的电压和相角，以确定电力系统的稳态工作状态。由于电力系统的非线性特性，潮流计算问题可以建模为一个非线性方程组，其中包含了大量的功率平衡方程和节点电压方程。牛顿迭代法可以应用于求解这些非线性方程组，以实现电力系统的潮流计算。未来随着电力系统的智能化和高效化发展，牛顿迭代法在电力系统工程中的应用也将更加广泛，可能会涉及到电力系统的实时运行优化、智能调度等方面。
结构工程：在结构工程中，牛顿迭代法被广泛应用于结构分析和设计。结构工程涉及到建筑物、桥梁、飞机等各种结构的设计和分析，其中包含了大量的非线性问题，如弹性力学、塑性力学、非线性材料等。牛顿迭代法可以应用于求解这些非线性问题，以确定结构的受力状态、变形情况或者稳定性分析。未来随着结构工程的发展，牛顿迭代法可能会在更复杂的结构分析和设计中得到应用，比如在微观尺度下考虑材料的非线性行为、多物理场耦合等方面。
控制系统设计：在控制工程中，牛顿迭代法被应用于控制系统的设计和优化。控制工程涉及到控制系统的建模、分析和设计，其中包含了大量的非线性问题，如非线性控制、非线性系统等。牛顿迭代法可以应用于求解这些非线性问题，以确定控制系统的参数或者设计控制策略。未来随着控制工程的发展，牛顿迭代法可能会在自适应控制、模糊控制、深度学习控制等方面发挥更重要的作用。。
结构力学分析：在结构力学中，需要解决非线性的力学方程，如弹性力学、塑性力学等。牛顿迭代法可以用于求解这些非线性方程，以确定结构的受力状态、变形情况或者稳定性分析。
信号处理：在信号处理领域，有时需要求解非线性方程来实现信号的滤波、降噪或者分析。牛顿迭代法可以应用于这些问题的求解，以实现对信号的处理与分析。
数值优化：牛顿迭代法也可以用于求解优化问题，特别是在数值优化中，需要最小化或者最大化目标函数的情况下。通过求解目标函数的导数和二阶导数，可以利用牛顿迭代法来寻找最优解。

随着科学技术的不断进步和工程领域的不断发展，牛顿迭代法在实际工程问题中的应用前景是十分广阔的。未来我们可以期待牛顿迭代法在工程领域中的应用更加普遍和深入，可能会涉及到更多领域的问题求解和优化，比如在智能交通系统、智能制造系统、智能能源系统等方面的应用。同时，随着计算机硬件和软件技术的不断发展，牛顿迭代法的计算效率和稳定性也会得到进一步提高，为工程领域的应用提供更加可靠和高效的解决方案。因此，牛顿迭代法作为一种强大的数值方法，将继续在工程领域中发挥重要作用，推动工程技术的进步和发展。

五.可执行文件和源代码

源代码Gitee仓库地址：牛顿迭代法演示程序源代码-Gitee仓库地址
代码：

"""
@author: 观止
@complete: 2024-06-08
"""
import sys

import matplotlib.pyplot as plt
import numpy as np
from PyQt5.QtWidgets import (
    QApplication, QMainWindow, QWidget, QVBoxLayout, QHBoxLayout,
    QLabel, QLineEdit, QPushButton, QTextEdit, QMessageBox,
)
from matplotlib.backends.backend_qt5agg import FigureCanvasQTAgg as FigureCanvas
from sympy import *

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号


class FunctionPlotterApp(QMainWindow):
    function_placeholder = "请输入,参考使用帮助"
    initial_guess_placeholder = "请输入,例如0"
    error_placeholder = "请输入,例如0.0005"
    precision_placeholder = "请输入,例如8"
    max_placeholder = "请输入,例如10"

    def __init__(self):
        super().__init__()
        self.setWindowTitle("关于一元方程求根中牛顿迭代法的分析")

        central_widget = QWidget()
        self.setCentralWidget(central_widget)
        layout = QVBoxLayout(central_widget)

        # 输入框布局
        input_layout = QHBoxLayout()
        layout.addLayout(input_layout)

        # 函数输入框
        self.function_entry = QLineEdit(self)
        self.function_entry.setPlaceholderText(self.function_placeholder)
        self.function_entry.textChanged.connect(self.reset_button_and_image)
        input_layout.addWidget(QLabel("函数表达式："))
        input_layout.addWidget(self.function_entry)

        # 初始猜测值输入框
        self.initial_guess_entry = QLineEdit(self)
        self.initial_guess_entry.setPlaceholderText(self.initial_guess_placeholder)
        self.initial_guess_entry.textChanged.connect(self.reset_button_and_image)
        input_layout.addWidget(QLabel("初始猜测值："))
        input_layout.addWidget(self.initial_guess_entry)

        # 误差输入框
        self.error_entry = QLineEdit(self)
        self.error_entry.setPlaceholderText(self.error_placeholder)
        self.error_entry.textChanged.connect(self.reset_button_and_image)
        input_layout.addWidget(QLabel("误差："))
        input_layout.addWidget(self.error_entry)

        # 显示精度位输入框
        self.precision_entry = QLineEdit(self)
        self.precision_entry.setPlaceholderText(self.precision_placeholder)
        self.precision_entry.textChanged.connect(self.reset_button_and_image)
        input_layout.addWidget(QLabel("显示精度位："))
        input_layout.addWidget(self.precision_entry)

        # 最大迭代次数输入框
        self.max_entry = QLineEdit(self)
        self.max_entry.setPlaceholderText(self.max_placeholder)
        self.max_entry.textChanged.connect(self.reset_button_and_image)
        input_layout.addWidget(QLabel("最大迭代次数："))
        input_layout.addWidget(self.max_entry)

        # 按钮布局
        button_layout = QHBoxLayout()
        layout.addLayout(button_layout)

        # 绘制函数按钮
        self.start_button = QPushButton("绘制函数")
        self.start_button.clicked.connect(self.start_plot_function)
        button_layout.addWidget(self.start_button)

        # 逐步迭代按钮
        self.iterate_button = QPushButton("逐步迭代")
        self.iterate_button.clicked.connect(lambda: self.plot_iteration(False))
        self.iterate_button.setEnabled(False)
        button_layout.addWidget(self.iterate_button)

        # 一键迭代按钮
        self.show_result_button = QPushButton("一键迭代")
        self.show_result_button.clicked.connect(lambda: self.plot_iteration(True))
        self.show_result_button.setEnabled(False)
        button_layout.addWidget(self.show_result_button)

        # 使用帮助按钮
        self.help_button = QPushButton("使用帮助")
        self.help_button.clicked.connect(self.show_help)
        button_layout.addWidget(self.help_button)

        # 重置程序按钮
        self.reset_button = QPushButton("重置程序")
        self.reset_button.clicked.connect(self.reset_option)
        button_layout.addWidget(self.reset_button)

        # 图形显示布局
        graph_layout = QHBoxLayout()
        layout.addLayout(graph_layout)

        # 第一个绘图区域
        self.figure1 = plt.figure(figsize=(6, 4))
        self.canvas1 = FigureCanvas(self.figure1)
        graph_layout.addWidget(self.canvas1)
        layout.setStretchFactor(self.canvas1, 10)  # 设置画布在布局中的拉伸因子
        # 连接画布的事件到相应的方法
        self.canvas1.mpl_connect("scroll_event", self.zoom)
        self.canvas1.mpl_connect("button_press_event", self.on_press)
        self.canvas1.mpl_connect("button_release_event", self.on_release)
        self.canvas1.mpl_connect("motion_notify_event", self.on_motion)
        self.dragging = False  # 设置拖动标志
        self.last_mouse_pos = None  # 初始化上一个鼠标位置

        # 第二个绘图区域
        self.figure2 = plt.figure(figsize=(6, 4))
        self.canvas2 = FigureCanvas(self.figure2)
        graph_layout.addWidget(self.canvas2)

        # 迭代结果显示框
        self.iteration_result_text = QTextEdit()
        layout.addWidget(self.iteration_result_text)

    def adjust_axes(self):  # 定义调整坐标轴范围的方法
        xlim = self.ax1.get_xlim()  # 获取 x 轴范围
        ylim = self.ax1.get_ylim()  # 获取 y 轴范围
        x_range = xlim[1] - xlim[0]  # 计算 x 轴范围
        y_range = ylim[1] - ylim[0]  # 计算 y 轴范围
        if x_range > y_range:  # 若 x 轴范围大于 y 轴范围
            y_center = (ylim[1] + ylim[0]) / 2  # 计算 y 轴中心
            new_y_range = x_range  # 新的 y 轴范围为 x 轴范围
            self.ax1.set_ylim(y_center - new_y_range / 2, y_center + new_y_range / 2)  # 设置新的 y 轴范围
        else:  # 若 y 轴范围大于等于 x 轴范围
            x_center = (xlim[1] + xlim[0]) / 2  # 计算 x 轴中心
            new_x_range = y_range  # 新的 x 轴范围为 y 轴范围
            self.ax1.set_xlim(x_center - new_x_range / 2, x_center + new_x_range / 2)  # 设置新的 x 轴范围

    def zoom(self, event):  # 定义缩放方法
        base_scale = 1.1  # 缩放基础比例
        scale_factor = 1 / base_scale if event.button == 'up' else base_scale  # 计算缩放因子

        xdata = event.xdata  # 获取事件的 x 数据
        ydata = event.ydata  # 获取事件的 y 数据
        if xdata is None or ydata is None:  # 若数据为空，则返回
            return

        xlim = self.ax1.get_xlim()  # 获取 x 轴范围
        ylim = self.ax1.get_ylim()  # 获取 y 轴范围
        x_range = (xlim[1] - xlim[0]) * scale_factor  # 计算新的 x 轴范围
        y_range = (ylim[1] - ylim[0]) * scale_factor  # 计算新的 y 轴范围

        x_center = (xlim[0] + xlim[1]) / 2  # 计算 x 轴中心
        y_center = (ylim[0] + ylim[1]) / 2  # 计算 y 轴中心

        # 设置新的 x 和 y 轴范围
        self.ax1.set_xlim([x_center - x_range / 2, x_center + x_range / 2])
        self.ax1.set_ylim([y_center - y_range / 2, y_center + y_range / 2])
        self.adjust_axes()  # 调整坐标轴范围
        self.canvas1.draw_idle()  # 重新绘制图表

    def on_press(self, event):  # 定义鼠标按下事件处理方法
        if event.button == 1:  # 若为左键按下
            self.dragging = True  # 设置拖动标志为 True
            self.last_mouse_pos = (event.x, event.y)  # 记录当前鼠标位置

    def on_release(self, event):  # 定义鼠标释放事件处理方法
        if event.button == 1:  # 若为左键释放
            self.dragging = False  # 设置拖动标志为 False
            self.last_mouse_pos = None  # 清空鼠标位置

    def on_motion(self, event):  # 定义鼠标移动事件处理方法
        if self.dragging and event.xdata is not None and event.ydata is not None:  # 若正在拖动且鼠标位置有效
            dx = event.x - self.last_mouse_pos[0]  # 计算 x 方向位移
            dy = event.y - self.last_mouse_pos[1]  # 计算 y 方向位移

            xlim = self.ax1.get_xlim()  # 获取 x 轴范围
            ylim = self.ax1.get_ylim()  # 获取 y 轴范围
            width, height = self.canvas1.get_width_height()  # 获取画布宽度和高度
            dx_data = dx * (xlim[1] - xlim[0]) / width  # 计算 x 方向的数据位移
            dy_data = dy * (ylim[1] - ylim[0]) / height  # 计算 y 方向的数据位移

            # 更新 x 和 y 轴范围
            self.ax1.set_xlim(xlim[0] - dx_data, xlim[1] - dx_data)
            self.ax1.set_ylim(ylim[0] - dy_data, ylim[1] - dy_data)
            self.last_mouse_pos = (event.x, event.y)  # 更新鼠标位置
            self.adjust_axes()  # 调整坐标轴范围
            self.canvas1.draw_idle()  # 重新绘制图表

    # 输入值变化重置按钮状态和图像
    def reset_button_and_image(self):
        # 禁用按钮
        self.iterate_button.setEnabled(False)
        self.show_result_button.setEnabled(False)
        # 重置界面
        self.figure1.clear()
        self.canvas1.draw()
        self.figure2.clear()
        self.canvas2.draw()
        # 清空结果显示框
        self.iteration_result_text.clear()
        # 重置迭代次数
        self.count = 1

    def start_plot_function(self):
        # 参数校验
        if not self.valid_param():
            return
        # 启用按钮
        self.iterate_button.setEnabled(True)
        self.show_result_button.setEnabled(True)
        # 定义变量
        x = Symbol('x')
        # 定义函数
        self.f_expr = eval(self.function_entry.text())
        self.f = lambdify(x, self.f_expr)
        # 求一阶导数
        self.df_expr = diff(self.f_expr, x)
        self.df = lambdify(x, self.df_expr)
        # 清除第一个绘图区域
        self.figure1.clear()
        self.ax1 = self.figure1.add_subplot(111)
        x_range_extension = 1  # 可以调整 x 轴范围
        X = np.linspace(float(self.initial_guess_entry.text()) - x_range_extension,
                        float(self.initial_guess_entry.text()) + x_range_extension, 1000000)
        self.ax1.set_title('函数表达式参考图像')  # 添加标题
        # 绘制函数图像
        self.ax1.plot(X, self.f(X), 'green', label="函数表达式")
        # 在图表上绘制函数图像和辅助线
        self.ax1.axhline(0, color='black', linestyle="--", linewidth=0.5)
        self.ax1.axvline(0, color='black', linestyle="--", linewidth=0.5)
        self.ax1.legend()
        self.ax1.grid(True)
        # 刷新第一个绘图区域
        self.canvas1.draw()
        self.result, self.num, self.All = self.Newton(float(self.initial_guess_entry.text()),
                                                      float(self.error_entry.text()), int(self.max_entry.text()))
        # 标明迭代次数
        self.count = 1

    def reset_option(self):
        # 重置所有输入框
        self.function_entry.clear()
        self.initial_guess_entry.clear()
        self.error_entry.clear()
        self.precision_entry.clear()
        self.max_entry.clear()
        # 禁用按钮
        self.iterate_button.setEnabled(False)
        self.show_result_button.setEnabled(False)
        # 清空图形区域
        self.figure1.clear()
        self.canvas1.draw()
        self.figure2.clear()
        self.canvas2.draw()
        # 清空结果显示框
        self.iteration_result_text.clear()
        # 重置迭代次数
        self.count = 1

    # 牛顿法(输入三个参数，初始猜值、误差、最大迭代次数)
    def Newton(self, x0, E, max_count=100):
        ans_list = [x0]  # 存放迭代过程中的所有解
        for i in range(max_count):  # 最大迭代次数
            ans_list.append(ans_list[i] - self.f(ans_list[i]) / self.df(ans_list[i]))  # 迭代公式
            if abs(ans_list[i + 1] - ans_list[i]) <= E:
                break
        # 返回最终迭代结果，迭代次数，迭代过程全解
        return ans_list[i + 1], i + 1, ans_list

    def plot_iteration(self, show_all):
        # 判断类型
        if show_all:
            data = self.All
            self.count = 1
        else:
            if self.count == len(self.All) + 1:
                self.show_error("已结束", "迭代次数已达到最大值")
                return
            data = self.All[:self.count]
            self.count += 1
        # 清除第二个绘图区域
        self.figure2.clear()
        ax2 = self.figure2.add_subplot(111)
        ax2.set_title('迭代值变化图像')  # 添加标题
        # 绘制迭代过程图像
        self.update_result(data)
        ax2.plot(np.arange(0, len(data), 1), data, '#bcbd22', linestyle='-',
                 label="迭代过程", marker='o', markersize=6,
                 markeredgecolor='black', markerfacecolor='red')
        ax2.set_ylabel('迭代数值')
        ax2.set_xlabel('迭代次数')
        # 在每个点上添加数值
        for i, txt in enumerate(data):
            ax2.text(i, txt, f'{txt:.{self.precision_entry.text()}f}', fontsize=8, verticalalignment='bottom',
                     horizontalalignment='right')
        ax2.legend()
        ax2.grid(True)
        # 刷新第二个绘图区域
        self.canvas2.draw()

        # 绘制迭代过程图像
        for x_current in data:  # 进行迭代
            y_current = self.f(x_current)  # 计算当前点的函数值
            y_prime_current = self.df(x_current)  # 计算当前点的导数值
            x_next = x_current - y_current / y_prime_current  # 计算下一个点的位置
            # 在图表上绘制迭代过程中的点和连线
            self.ax1.plot([x_current, x_next], [y_current, 0], 'ro-')
            self.ax1.plot([x_next, x_next], [0, self.f(x_next)], 'g--')
        self.canvas1.draw()  # 重新绘制图表

    def update_result(self, temp):
        # 更新迭代结果文本框内容
        self.iteration_result_text.clear()
        self.iteration_result_text.append(f"迭代过程：")

        for i, val in enumerate(temp):
            if i == 0:
                self.iteration_result_text.append(f"初始猜测值：x = {val:.{self.precision_entry.text()}f}")
            else:
                self.iteration_result_text.append(f"第{i}次迭代：x = {val:.{self.precision_entry.text()}f}")
            if i == self.num:
                self.iteration_result_text.append(
                    f"======\n迭代结束:\n方程的一个实根为x = {val:.{self.precision_entry.text()}f} \n迭代次数： {self.num}")

    def show_help(self):
        help_message = (
            "欢迎使用一元方程求根中牛顿迭代法的分析程序！\n\n"
            "以下是每个输入框和按钮的作用以及输入函数的格式要求：\n\n"
            "- 函数表达式输入框：\n"
            "  请输入一个数学函数表达式，例如：x**2 + 3*x - 5、exp(x) + 10*x - 2。\n"
            "  表达式应当符合python语法，如加法(+), 减法(-), 乘法(*), 除法(/), 幂(**)。 \n"
            "  特殊函数输入格式请参考SymPy官方文档，例如e^x => exp(x)\n"
            "  SymPy官方文档：https://docs.sympy.org/latest/tutorials/intro-tutorial/index.html#intro-tutorial\n"
            "  Python语法学习：https://blog.csdn.net/m0_66570338/article/details/128714062\n\n"
            "- 初始猜测值输入框：\n"
            "  输入一个初始猜测值，作为迭代计算的起始点。\n"
            "  可以输入整数或小数。\n\n"
            "- 误差输入框：\n"
            "  输入一个用于判断迭代精度的误差值。\n"
            "  当迭代结果与上一次迭代结果的差值小于误差时，迭代停止。\n\n"
            "- 显示精度位输入框：\n"
            "  设置迭代过程中结果的显示精度位数。\n"
            "  输入一个正整数，表示显示结果的小数位数。\n\n"
            "- 最大迭代次数输入框：\n"
            "  设置最大迭代次数，以避免迭代无限循环。\n"
            "  输入一个正整数，表示最大的迭代次数。\n\n"
            "- 绘制函数按钮：\n"
            "  根据输入的函数表达式，绘制函数图像。\n\n"
            "- 逐步迭代按钮：\n"
            "  逐步展示迭代过程的图像，并显示每次迭代的结果。\n\n"
            "- 一键迭代按钮：\n"
            "  一次性展示所有迭代过程的图像，并显示最终的迭代结果。\n\n"
            "- 重置程序按钮：\n"
            "  重置所有的操作记录，清空输入框和图像区域，恢复到初始状态。\n"
        )
        QMessageBox.information(self, "使用帮助", help_message, QMessageBox.Ok)

    def valid_param(self):
        # # 参数校验
        function_entry = self.function_entry.text()
        initial_guess_entry = self.initial_guess_entry.text()
        error_entry = self.error_entry.text()
        precision_entry = self.precision_entry.text()
        max_entry = self.max_entry.text()
        # 检查函数表达式
        if not self.function_entry.text():
            self.show_error("错误", "函数表达式输入有误，请仔细检查或参考帮助文档")
            return False
        else:
            try:
                x = Symbol('x')
                lambdify(x, eval(function_entry))
            except Exception as e:
                self.show_error("错误", "函数表达式输入有误，请仔细检查或参考帮助文档")
                print(e)
                return False
        # 检查初始猜测值
        if not initial_guess_entry:
            self.show_error("错误", "初始猜测值输入有误，请仔细检查或参考帮助文档")
            return False
        elif not initial_guess_entry.replace('.', '', 1).isdigit():
            self.show_error("错误", "初始猜测值输入有误，必须为小数或整数")
            return False
        # 检查误差
        if not error_entry:
            self.show_error("错误", "误差输入有误，请仔细检查")
            return False
        elif not error_entry.replace('.', '', 1).isdigit():
            self.show_error("错误", "误差输入有误，必须为小数或整数")
            return False
        # 检查迭代精度
        if not precision_entry:
            self.show_error("错误", "显示精度位输入有误，请仔细检查")
            return False
        elif not precision_entry.isdigit():
            self.show_error("错误", "显示精度位输入有误，必须为整数")
            return False
        elif int(precision_entry) <= 0:
            self.show_error("错误", "显示精度位输入有误，必须大于0")
            return False
        # 检查最大迭代次数
        if not max_entry:
            self.show_error("错误", "最大迭代次数输入有误，请仔细检查")
            return False
        elif not max_entry.isdigit():
            self.show_error("错误", "最大迭代次数输入有误，必须为整数")
            return False
        elif int(max_entry) <= 0:
            self.show_error("错误", "迭代精度位输入有误，必须大于0")
            return False
        return True

    def show_error(self, title, message):
        QMessageBox.critical(self, title, message, QMessageBox.Ok)


if __name__ == '__main__':
    app = QApplication(sys.argv)
    window = FunctionPlotterApp()
    window.show()
    sys.exit(app.exec_())

观止study

关注

11
点赞
踩
16

收藏

觉得还不错? 一键收藏
打赏
0
评论
关于一元方程求根中牛顿迭代法的分析

【大三下数值分析课程设计】关于一元方程求根中牛顿迭代法的分析相关可执行Pyhon源代码~牛顿迭代法（Newton's Method），也称为牛顿-拉弗森方法（Newton-Raphson Method），是一种用于寻找函数零点或者说方程的根的迭代数值方法。它是一种非常有效的数值分析技术，具有收敛速度快的特点，通常用于求解实数域上的非线性方程，特别是在科学和工程领域中经常遇到的问题。
复制链接

扫一扫