最近在做对齐相关的工作,查资料时偶然查到了一个网站,感觉帮助很大,做个记录
1、一元多次多项式求根直接转化为 对伴随矩阵求特征值
2、里面有许多专题:傅里叶变换,奇异值分解,奇异值与特征值联系,KKT条件,马尔科夫等等,都值得一读
pageRank:PageRank
傅里叶变换:快速傅立葉轉換 傅里叶变换应该还有取模形式(精度),但是任意模数的实现资料有待查找
KKT条件:KKT条件
母函数:母函数
一个有趣的问题,矩阵乘链的计算顺序,看上去就是动态规划,粗想过去类似石子归并,是否有特殊性质更快方法,没接下去想:矩陣鏈乘積的最佳計算順序
循环矩阵:特殊矩陣七:循環矩陣
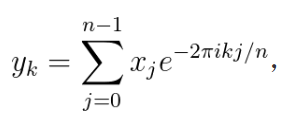



看了里面有篇FFT,然后就顺便复习了下,
对一个向量x做傅里叶变换得到向量y用矩阵表示就是,用一个傅里叶系数矩阵F乘向量x,即y=Fx,逆变换形式一样就是加了个共轭以及一个系数。
另,其跟循环矩阵有联系,循环矩阵的线性方程组不论是求逆还是矩阵乘向量,复杂度都是nlogn,这是因为循环矩阵比较特殊,可以分解为特征值特征向量形式,特征向量正交矩阵就是傅里叶变换系数矩阵乘个系数,特征值就是对矩阵第一行做个傅里叶变换。







 本文介绍了网站「線代啟示錄」中关于一元多项式求根、傅里叶变换、奇异值分解等专题内容,并探讨了傅里叶变换在矩阵运算中的应用,包括矩阵乘链的计算顺序问题和循环矩阵的特性。
本文介绍了网站「線代啟示錄」中关于一元多项式求根、傅里叶变换、奇异值分解等专题内容,并探讨了傅里叶变换在矩阵运算中的应用,包括矩阵乘链的计算顺序问题和循环矩阵的特性。
















 130
130

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








