查了一下,高维情形的证明应该涉及到 Random walk 的一些知识,维基百科里就写得还不错:Random_walk
当然,如果只是简单的一维情形的话,可以只用相关的推广意义下的卡特兰数的公式进行证明。
令推广的卡特兰数为
则,先从原点0出发,第一步无论向左还是向右先走一步。然后就是往该方向的卡特兰数了。
设又走了2n步,则有可能其中往回走了0-n步的推广的卡特兰数情形。
所以最后回不去原点的概率为

然后就是n趋向于无穷的情形了。(有新的问题可以想了,二项式系数的分布在趋向于无穷之后会是怎样的?其中二项式系数最大值与总和的比例是多少?)
总有印象曾经做出过高维情形的公式,但现在就是想不起来了,所以把自己的思考过程及时记录下来还是非常重要的!








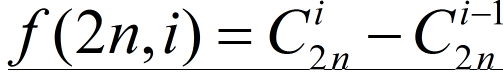















 4974
4974

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








