原文链接:
http://www.wildml.com/2015/11/understanding-convolutional-neural-networks-for-nlp/
原标题《Understanding convolutional neural networks for nlp》
当我们听到CNNs时,我们一般会想到计算机视觉(computer vision)。CNNs在图像分类中取得了重大突破,也是从Facebook的自动图像标注到自动驾驶等,当今计算机视觉系统的核心。
最近我们也开始尝试使用CNNs来解决NLP问题,并且取得了一些有趣的结果。在本贴中,我将会尝试着总结下CNNs是什么,并且它们是怎样被用到NLP中。计算机视觉的应用案例对CNNs有更加直观的理解,所以我会先从computer vision开始,一点点的延伸到NLP。
1.What is Convolution?
对我来说,最直观的理解一个convolution,是把它想象成一个应用在matrix的滑动窗口函数。这是一种口语化的表述,下面的示例图可以更加清晰明白:

上图中左边的矩阵表示的是一张黑白图像。每个方格代表了一个像素,0表示黑色,1表示白色(一般的灰度图像值是0到255之间,这里只是举个例子)。滑动窗口一般称为kernel,filter或者feature detector。这里我们使用的是一个3*3的filter,将它的值和与其对应的原图像矩阵进行相乘,然后再将它们相加。这样我们在整个原图矩阵上滑动filter来搜寻所有元素(像素)并得到一个完整的convolution。
例子:将一张图像中的每个像素值与其相邻的值做平均处理来得到一张模糊的图片:
2.What are Convolutional Neural Net Works?
现在你知道了convolution是什么,但CNNs呢?CNNs基本上是由几层convolutions做计算,再用一些类似ReLU和tanh的非线性激活函数应用在计算的结果上。在传统的前馈神经网络中,我们将每个输入神经元连接到下一层的每个输出神经元,这也称为全连接层或仿射层。在CNNs 中,我们并不这么做,我们使用convolutions来覆盖整个输入层并计算出输出。输入的每个局部区域会连接到输出中的的神经元,这样的连接属于局部连接。每层会使用不同的filters,如上面展示的filter会通常有成千上百个,并将这些filters的结果结合起来。也会有一些称为pooling(subsampling——二次抽样)的层,这些我后面会讲。在训练阶段,CNN会根据你提供的训练集自动学习这些filters的参数值。例如,在图像分类中,CNN在第一层可以从原始像素中检测到边缘,然后在第二层中使用边缘来发现一些简单的形状,然后在更高级层使用这些形状来发现一些类似脸部等这些高级别特征。最后一层是使用这些高级别特征做分类。

在计算中有两方面是值得关注的:位置不变性(Location Invariant)和组合性(Compositional)。假设你想判断一张图片中是否有一头大象,因为你正在整张图片上滑动你的filters,所以你并不在意这头大象会出现在图片的什么位置。在实践中,池化也会给你提供不变性的平移,旋转和缩放,但更多的是后者(即缩放)。第二个关键方面是(局部)组合性,每个filter会组成一个从低级特征到高级特征表示的局部patch。这也是为何CNNs在计算机视觉中如此强大的原因。你可以从直觉上理解,它是从像素到边缘,从边缘到形状,再从形状到更加复杂的对象。
3. So, How dose any of this apply to NLP ?
不同于图像的像素,大部分NLP任务的输入是句子或文档作为一个矩阵。矩阵的每一行表示一个token,一般是一个分词,但也可以是一个字,总之每行都是一个向量,代表一个word。一般这些向量会称为word embedding(low-dimensional representations),像word2vec 或 GloVe,当然了,它们也可以是one-hot向量。例如一个包含10个分词的sentence,每个分词使用一个100维的向量表示,那么我们就有一个10*100的矩阵作为我们的输入。这就是我们的“图”。
在视图中,我们的filters会在图像的局部滑动,但在NLP中,我们一般会使用filters在矩阵的整个行上滑动。所以我们filters的宽度通常是和输入矩阵的宽度是一致的。而高度(或称为区块尺寸(region size))是变化的,一般情况是每次的滑动窗口为2-5个words。将上面所有描述的总结起来,用于NLP的CNNs看起来是这样子的(花费几分钟来尝试着理解下图原理,并理解这些向量是怎么计算的。你现在可以先忽略pooling,我们在后面将会介绍):

该图描绘的是一个用于句子分类的CNNs架构。这里我们描绘了三个区块分别为2,3,4的filter,每类filter有两个,这样就有3*2 = 6个filter。每个filter都会从句子矩阵中做卷积并分别生成一个特征映射,然后在每个映射上执行1-max pooling,即记录下每个特征映射中的最明显特征。因此,从这六个映射中生成6个单变量特征向量,并将这6个单变量特征向量级联(concatenate)成一个特征向量作为倒数第二层。最后一层的soft max将生成的特征向量作为输入并用它来进行句子的分类。这里我们假设是二分类问题,因此描绘出两种可能的输出状态。Source: Zhang, Y., & Wallace, B. (2015). A Sensitivity Analysis of (and Practitioners’ Guide to) Convolutional Neural Networks for Sentence Classification.
我们对计算机视觉的直觉是什么?位置的不变性(Location Invariance)和局部的组合性(Local Compositionality)是对图像的直观感觉,但对NLP就不太是这样了。你可能会关心一个word出现在sentence的什么地方。相邻的像素之间会有语义的相关性(同一对象的一部分),但对于words来讲就不见得是这样。在一些语言中,部分短语可能会被words分割开。在组合性方面来看也不明显,虽然词语也存在这某些方面的构成,如形容词修饰名词,但在更高一层的表示上究竟是怎么工作的,实际上这里的思想不像在计算机视觉案例中那么明显。
根据以上描述,CNNs看起来在并不太适用于NLP任务。RNN相比起来会更加直观一些。RNN假设我们是按顺序从左到右处于语言的。但幸好,这并不能就意味这CNNs在NLP中没有成果。正如格言“ All models are wrong, but some are useful”,它也证明了CNNs在NLP的应用中也相当好。Bag of Words Model模型就是一个明显的例子,它使用错误的假设,过于简化,但尽管如此,它还是作为标准方法使用好多年,并取得了不错的效果。
CNNs的一个大争论是它们的计算是非常非常的快。因为convolutions是计算机图形计算的核心,并且在硬件上由GPUs实现。和类似n-grams这类东西相比,CNNs在表示方面也很有效。对于一个海量的词汇表,计算任何超过3-grams的东西都会变得非常昂贵,即使是谷歌也没有提供任何超过5-grams的东西。卷积filters可以自动学习好的表达,并且不需要表达出整个词汇表。在卷积中使用region size大于5的filters是完全合理的。我个人认为在第一层中的许多filters所捕获的特征与n-gram(但不限于n-gram)非常相似,但会以更加紧凑的方式表达它们。
4.CNN Hyperparameters
在解释CNNs是怎样应用到NLP任务中之前,让我们先看一下当你要构建CNN时所面临的选择。真心希望这会帮助你能更好的理解该领域的相关文献。
4.1 Narrow VS. Wide Convolution
当我在解释上面的卷积时,我忽略了一个细节:我们该如何申请一个filter。申请一个3*3的filter在矩阵的中心会工作的很好,但是在矩阵的边际会怎样呢?矩阵的第一个元素,其顶部和左边都没有相邻元素,你该如何将filter应用到这样的元素上?你可以使用zero-padding(0填充)所有落到矩阵以外的元素都将用0代替。这样你就可以将filter应用到你输入的任何矩阵中了,并且可以得到一个更大或等大的矩阵作为输出。添加zero-padding也被称为wide convolution,而不使用zero-padding的将称为narrow convolution。下图是一个1维的例子:

Narrow vs. Wide Convolution. Filter size 5, input size 7. Source: A Convolutional Neural Network for Modelling Sentences (2014)
当你的filter比输入的size还大时,你可以看到wide convolution是多么的有用,甚至说是必须的。如上所示,narrow convolution产出的尺寸是(7-5)+1=3,而wide convolution产出尺寸是(7+2*4-5)+1=11。通常,输出尺寸的规则表达式为:
4.2 Stride Size
另外一个convolution的超参数是Stride size,定义了你的filter在每步中滑动多少。上面提到的所有例子中都是默认为1,并且是连续重叠的应用filter。Stride size越大,filters的应用次数就会越少,输出的size就会越小。下图描述了Stride size分别为1和2,应用到1维的输入上:

Convolution Stride Size. Left: Stride size 1. Right: Stride size 2. Source: http://cs231n.github.io/convolutional-networks/
在上图我们可以看到一个典型的Stride Size为1的Convolution,而更大的Stride Size可以让你建立一个类似与RNN结构的模型,也就是看起来像一棵树。
4.3 Pooling Layers
Pooling layers 是CNNs的一个重要方面,一般会应用在convolutional layers之后。Pooling layers是对输入做二次抽样。最常见的方法是使用一个max操作对每个filter输出的结果进行池化。你没必要去池化整个矩阵,类似于convolutional layers中的filter,你也可以做一个窗口池,就像下图一样,做了一个最大池为2*2的窗口(但如上面视图所示,在NLP中,我们一般是完整的池化整个输出,对每个filter只产生一个单一的值)。

为什么要池化?有以下几个原因。
1.池化的一个重要性质就是它提供了一个固定的尺寸来输出矩阵,一般对分类来说,这是一个必须的要求。例如,你有1000个filters,然后你对每个filter都做最大化pooling,你就会得到1000维度的输出向量,这样就不用考虑你filter的size和你input的size。
2.池化的另一个性质是它可以减少输出的维度,并能够最大化的保持显著的信息。你可以认为每个filter都是用于检测一个特定的特征,假设一个filter是用来检测一条sentence中是否会出现“not amazing”这类否定词的,如果这个短语出现在了句子中的某一位置,应用该filter的结果是在这块儿区域会产生一个高值,而且其他区域会产生一个小值。通过最大化pooling后,你将会保存该特征是否出现在了sentence中的信息,但你也会失去它具体出现在什么地方的信息。那么位置信息就真的不重要吗?不是的!位置信息很重要!它有点类似于n-gram模型,在n-gram模型中,你虽然丢失了位置的全局信息,但你通过n-gram保存了局部信息,例如“not amazing”和“amazing not”的差别是很大的。
在图像识别中,pooling也提供了对图像平移和旋转的不变性。当你在池化图像的一个区域时,即使你将该图像平移或旋转了几个像素,输出也会是近似相同,因为最大化操作还是会在该区域输出一个相同的值。
4.4 Channels
最有一个我们需要理解的概念是Channels。Channels是你输入数据的不同“视角”。例如,在图像识别中,你一般会有RGB(红,绿,蓝)三个channels。你可以在不同的channels上应用具有不同或相同权重的卷积。在NLP中,你也可以想象有各种channels:你可以用不同的词嵌入channel(例如word2vec和GloVe);你可以对同一条sentence用不同的语言表示,或者将其用不同的方式进行分段。









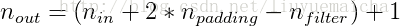














 7761
7761

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








