在lucene4以前,一直都是使用经典的向量空间模型作为其检索模型,这种方式虽然统一了评分算法,简化了计算,但是带来的问题是很难去调整,一旦向量空间模型不适合,也很难去替换一种更好的算法。
而lucene4则将检索模型与事实上的搜索做了解耦和抽象,并且加入了另外几种检索模型的实现,其中就有经典的BM25。
经典的向量空间模型的理论基础及其在lucene中的应用
向量空间模型是信息检索领域中一种成熟和基础的检索模型。这种方法以3维空间中的向量作为类比,维度就是做好索引的term,比如这里以3个主要的关键词奥巴马,叙利亚和战争为三个维度,通过文档在各个维度上的权重,每个文档以及查询都会在空间中有一个向量,直观的看起来,两个向量越相似,则他们的夹角越小,所以,用起反比的cos,则可以得到,cos值越大,则两个向量越相似。同理便可以将3维空间推广到多维空间去。
用向量空间模型,便将相关性转化为相似性,根据点积和模的定义,可以得到下式:
现在的问题就变成,如何求得每个维度上的term在文档中的权重,在向量空间模型中,特征权重的计算框架是TF*IDF框架,这里TF就是term在文档中的词频,TF值越大,说明该篇文档相对于这个term来说更加重要,因此,权重应该更高;而IDF则是term在整个文档集中占的比重,即n/N,其中n是含该term的文档数,N是总文档数,但是,实际使用中往往习惯用
即所包含的该term的文档数越少说明该term越重要。可以举个例子,有100篇文档,其中80篇都在说红楼梦,其中只有几篇讲到计算机,当你在这个文档集中搜索到计算机时,可以肯定这几篇讲计算机的比较重要,而搜索红楼梦时,则很难区分哪篇更加重要,换句话说,在这个文档集合中,计算机比红楼梦更有区分度,相对来说,计算机比红楼梦更有信息量,所以IDF就是评判所含信息量大小的一个值。
一般情况,使用TF*IDF作为这里的权重w,从而计算出dj,q的相似度sim(dj,q)。
那么,在lucene中,是如何应用这个模型的呢?根据向量空间模型的的数学推导(见参考文档3),可以看到,在lucene中实际上是将sim(dj,q)变形和调整后应用了如下一个打分公式
该公式各项参数解释如下,在DefaultSimilarity中都有每一项参数的基本定义:








 本文详细分析了Lucene 4.5中向量空间模型的评分算法,包括TF-IDF权重计算、协调因子、查询规范化等,探讨了这些因素如何影响文档的评分和排序。通过对源码的解读,揭示了Lucene如何组织和调整评分公式以适应不同的检索需求。
本文详细分析了Lucene 4.5中向量空间模型的评分算法,包括TF-IDF权重计算、协调因子、查询规范化等,探讨了这些因素如何影响文档的评分和排序。通过对源码的解读,揭示了Lucene如何组织和调整评分公式以适应不同的检索需求。
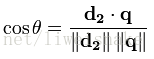
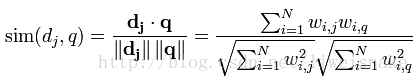

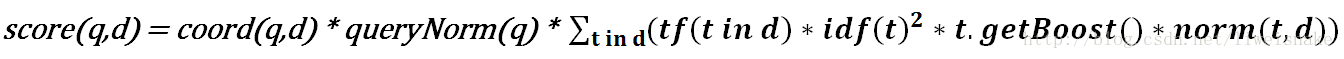
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 3024
3024

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








