1、傅里叶变换
将信号分解为多个不同频率的正弦波叠加,表示为:

每个正弦波的权值为
。
同理,可以表示为:
![]()
通过傅里叶变换与反变换可知,信号的频谱或功率谱只能用来表示某个频率上拥有的分量,因此可以分析平稳信号。然而,信号在某频率出现的时间也不能知晓,因此不适用于信号频率是时变函数的非平稳信号。
在跳频通信中,信号的载频以一定规律在一组频率集中不断“随机”跳动,是典型的非平稳信号。因此需要能够反映信号局部信息的变换。
时频变换构造”时间“-”频率“的二维平面,是分析非平稳信号的重要手段。
注:下面给出平稳信号、非平稳信号的简单理解:
平稳信号:信号的分布参数或者分布规律不随时间发生变化。例如,信号的频率不随着时间而变化。
非平稳信号:信号的分布参数或分布规律随时间发生变化。
2、短时傅里叶变换
(1)STFT的原理
连续信号的短时傅里叶变换表达式为:

上式可以看做信号x(τ) 被窗函数h*(τ) 截取后再进行傅里叶变换;即在该窗函数长度内,认为信号是x(t) 近似平稳的。接着平移窗函数,对x(t) 进行再一次的截取与傅里叶变换,最后将这些傅里叶变换进行累加便得到了STFT。
离散信号的短时傅里叶变换表达式为:
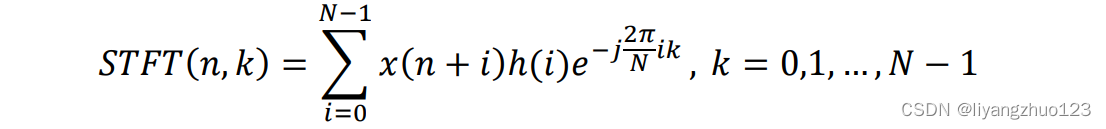
其中n 表示离散采样点,k表示离散频率点或者信道编号,h(i)表示窗函数,N表示窗函数长度,STFT(n,k)表示n 时刻、频率点k上的时频幅值强度。
如图7所示,在采样率为50KHz下,总共采样1024个点,每个跳周期内采样点数 N=256个,共截取了4跳信号。窗函数采Hamming(汉明)窗,窗长H=N/4+1=257,窗滑动步长为1。在上述参数设置下,得到的两个同步电台的短时傅里叶变换等高线图如下所示。
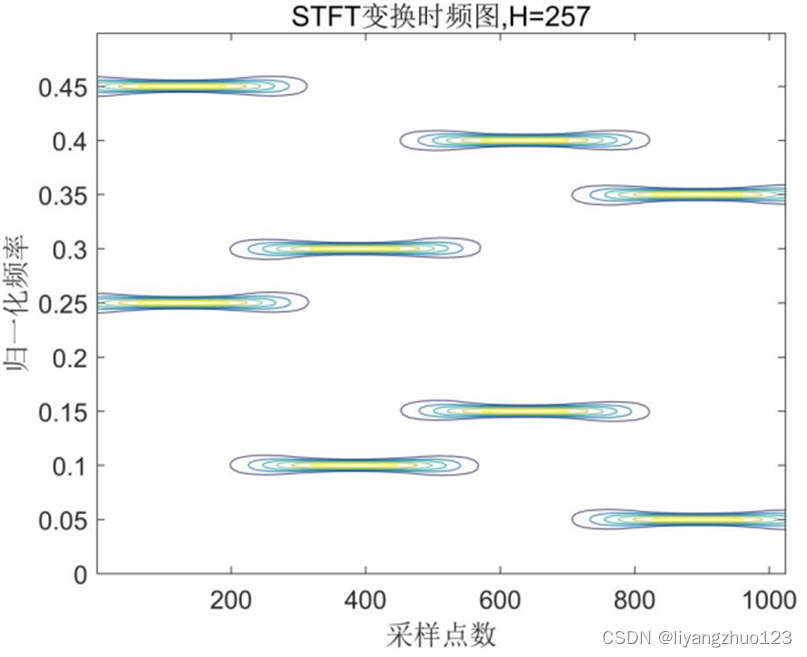
对于STFT来说,窗函数的长度的选择对于时域频域分辨性能有着极大的影响。
当选择较窄的窗长时,拥有很好的时间分辨率,但由于分析的点数很少,导致频率分辨率较低。反之,选择较宽的窗长时,分析的点数较多,频率分辨率提升,对应地时间分辨率则会下降。
对于上面这一段话,我的更深入的理解是:较窄的窗长意味着每次进行傅里叶变换时,只观察信号的一个较短的片段。这样,当信号中的事件(如频率变化、振幅变化等)在时间上相距较近时,使用较窄的窗长可以更容易地分辨这些事件。然而,较窄的窗长提高了时间分辨率,但可能会降低频率分辨率。因为较短的信号片段可能不包含足够的周期来准确估计频率成分。相反,较宽的窗长可以提高频率分辨率,但会降低时间分辨率。
对于STFT来说,时间分辨率和频率分辨率是难以做到两全其美的,在选择窗的长度时,应根据分析目标具体需求进行取舍。
对于快跳频信号与慢跳频信号,我们可以有如下两种不同的信号处理思路:
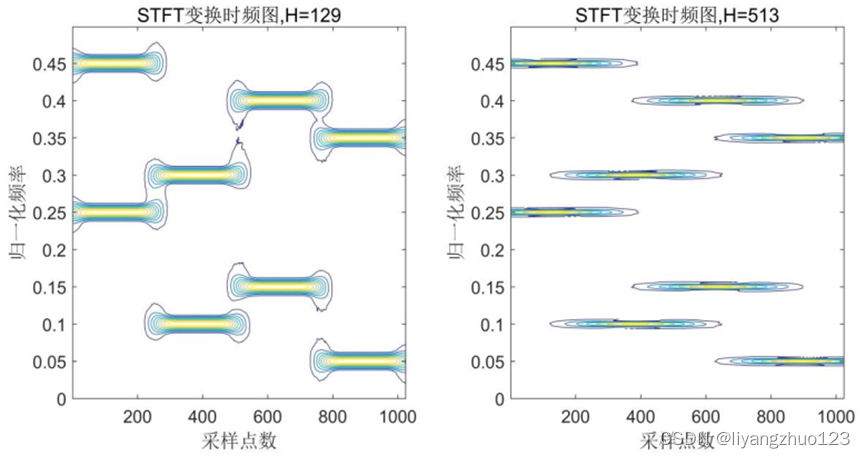
处理慢跳频信号:可以将窗长增加,这样虽然会使得时间分辨率下降,但频率分辨率会有所提升。如图8所示。
处理快跳频信号:要求时间分辨率较高,因此一般采用短窗进行处理。如图8所示。
(2)时间分辨率、频率分辨率
以下内容部分参考知乎的这篇文章:《信号的时间域分辨率和频率域分辨率 - 知乎》
时间分辨率:时域图横坐标上的最小时间间隔。其大小代表着对模拟信号采样后得到的离散信号中点的密集程度。数学公式为:。其数值越低,时间分辨率越高。提高时间域分辨率主要通过提高对信号的时间域采样率来实现。
频率分辨率:频谱图横坐标上的最小频率间隔。数学公式为:

提高频率分辨率的方法有几种,大致可以分为以下几种类型:

增加时域窗长来提高频率分辨率的效果,如下图所示:

最上面一幅图是函数为
y0=0.5*sin(2*pi*f1/fs*n)+0.5*sin(2*pi*f2/fs*n),
即2个频率分别为100Hz和150Hz单频音叠加的函数。理论上,FFT分析可以分辨出这两个频率,第二幅图是对这个信号频率能量谱的分析,其中窗长为50,可以看出,在频率80到180Hz形成了一个高大峰,未能区分出来这两个单频音峰;第三幅图为窗长提高到100点以后的信号频率能量谱,从该图可以看出,两个峰被分开了。
在实际应用中,可能无法提高时间域窗长,特别是对于持续时间比较短的信号。这种情况也可以直接增加频率域采样率。效果如下:

最上面一幅图是函数为
y0=0.5*sin(2*pi*f1/fs*n)+0.5*sin(2*pi*f2/fs*n),
即2个频率分别为100Hz和150Hz单频音叠加的函数。理论上,FFT分析可以分辨出这两个频率,第二幅图是对这个信号频率能量谱的分析,其中频率域采样点数为50点,可以看出,在频率80到180Hz形成了一个高大峰,未能区分出来这两个单频音峰;第三幅图为时间域采样点数不增加(时间域采样信号后补0以占位,实际上补1也可以,这不会对交流成分产生影响,但会对计算量产生影响),仅频率域采样点数提高到128点以后的信号频率能量谱,从该图可以看出,两个峰被分开了。
上述的两种方法都提高了频率域分辨率,这两种方法提高频率域分辨率的理论基础如下:离散傅里叶变换DFT实际上是对序列傅里叶变换在单周期的等间隔取样,在时间域采样满足奈奎斯特采样定理时,理论上频谱是没有混叠的,只要对序列傅里叶变换进行适当的采样就可以分辨出感兴趣的功率峰。由于序列的傅里叶变换是个连续周期谱,对该谱主值区间采样率越高,就能得到越精细的分辨率。如下图所示:

最上面一幅图是函数为
y0=0.5*sin(2*pi*f1/fs*n)+0.5*sin(2*pi*f2/fs*n),即2个频率分别为100Hz和150Hz单频音叠加的函数。第二幅图是序列傅里叶变换的主值区间,它是个连续谱,DTF是对该谱等间隔取样谱,其中图三按照50点对其进行取样,因为取样点过于“稀松”,故没有取到功率峰值点,也没有取到两个功率峰中间的谷值点,因此看起来这两个功率峰“叠”在一起;第四幅图按照128点取值,频率域采样率提高了约2倍,可以取到两个功率峰中的谷值(有偏差)点,每个功率峰也由原来的一个点增加到两个点,因此看起来两个功率峰被分开了。
那么,通过方法2(直接增加频率域采样率)和通过方法1(增加时间域窗长)看起来是等效的,因为他们实际上都增加了频率域采样率,他们区别又在哪里呢?结果见下图:

最上面一幅图是函数为
y0=0.5*sin(2*pi*f1/fs*n)+0.5*sin(2*pi*f2/fs*n),即2个频率分别为100Hz和150Hz单频音叠加的函数。第二幅图是在时间域采样点数不变的情况下,增加频率域采样点数的频谱图;图三是增加时间域窗长的频谱图。可见,图三的频谱更加“细腻”,在上图中未发现旁瓣和波纹,分辨效果较好。此外,图三的峰值幅度高于图二的峰值幅度。
这些现象的理论基础如下:时间域窗长不变时,序列傅里叶变换的频谱不变,由于矩形窗的存在的频率泄露效应,存在较大的旁瓣和主峰外波纹。图三实际上是提高了矩形窗窗长,因而减小了过渡带,降低了旁瓣和主峰外波纹(比例实际上未发生变化)。而对于峰值的影响,根据离散帕斯瓦尔定理,变换不会影响两个域的总能量,图二在时间域后补0,图三加大时间域窗长捕获的是实际信号,其能量要大于补0所获取的交流能量,因而其功率谱峰值比图二要高。
疑惑:图2在时间域后补0,具体是什么意思?
答:可以这么理解,图2是FFT点数为256的情况,倘若实际的时域数据点数不满足256(假设时域数据点数为200),为了使得做FFT的点数是256(一般让FFT的点数是2的整数次幂,这是为了傅里叶变换进行快速算法),因此需要在第201个点到第256个点补0,对补0后的时域数据段进行FFT。(为什么不是补1:为了降低计算量,补0的计算量比补1的计算量更小)
另外一种提高频率域分辨率的方法就是降低时间域采样率,效果如下图所示:

最上面一幅图是函数为:
y0=0.5*sin(2*pi*f1/fs*n)+0.5*sin(2*pi*f2/fs*n),即2个频率分别为100Hz和150Hz单频音叠加的函数。第二幅图是时间域采样率为2.5ksps时谱图,第三幅图是时间域采样率为0.5ksps时谱图。观察发现,降低时间域采样率后,可以明显看到100Hz功率谱峰和150Hz功率谱峰。
降低时间域采样率提高频率域分辨率的理论基础如下:在采样点数一定的情况下,采样频率越低,采出来的信号时间长度T0就越长,所以DFT的频率采样点间隔=1/T0也就越小。
我对上面这一段话的理解:降低时间分辨率,可以看作提高频域分辨率。
以上关于时间分辨率和频率分辨率的部分内容,介绍了信号的时间域分辨率和频率域分辨率关系及如何提高这些分辨率。提高时间域采样率可以提高时间域分辨率,但会降低频率域分辨率,这看起来很矛盾,但确实是这样。而如果既要提高时间域分辨率又要提高频率域分辨率则需要通过加大窗长来平衡这种需求,而加大窗长又会引起时间域采样时间的延长和更多的计算量。这也是为什么在使用频谱仪时,设置过小的频率分辨率和较高的采样率时,需要更多的获取时间才能刷新一帧图像。
3、谱图
谱图(Spectrogram, SP)可以看作STFT模的平方,也属于二次分布,表达式如下:
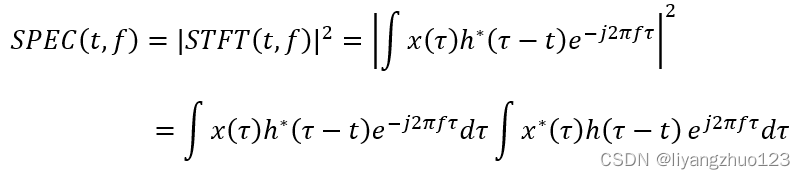
谱图作为非线性变换,拥有STFT变换算法简单,显示效果较好,硬件实现容易的特点。
针对多电台跳频信号,谱图是一种简单易行并且具有高可靠性的时频分析方式。
关于谱图的matlab实现,这里推荐自己根据公式画出时频矩阵,印象更加深刻,尽管matlab中已有现成的绘制谱图的函数spectrogram。







 文章探讨了傅里叶变换在信号处理中的应用,重点介绍了短时傅里叶变换如何分析非平稳信号,包括其原理、窗口函数的选择对时间分辨率和频率分辨率的影响,以及如何通过改变窗长来平衡两者。文中还提到谱图作为STFT的非线性变换在多电台跳频信号分析中的优势。
文章探讨了傅里叶变换在信号处理中的应用,重点介绍了短时傅里叶变换如何分析非平稳信号,包括其原理、窗口函数的选择对时间分辨率和频率分辨率的影响,以及如何通过改变窗长来平衡两者。文中还提到谱图作为STFT的非线性变换在多电台跳频信号分析中的优势。
















 4967
4967

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








