Robotics学习笔记基础---刚体转动

Robotics学习笔记基础—刚体转动（1）

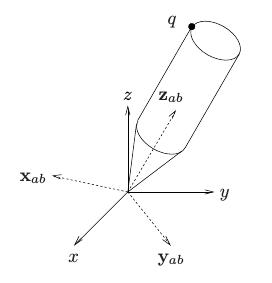
如图所示，$xyz$为参考坐标系（惯性系，记为A），$x_{ab}y_{ab}z_{ab}$为固连在刚体上的坐标系（即刚体的本体坐标系，记为B），本文所有的坐标系均为右手系，B相对于A的旋转矩阵用3x3的矩阵来描述，即：

$$R_{ab}=[x_{ab} y_{ab} z_{ab}]$$

旋转矩阵的性质：
旋转矩阵有两个重要的性质， $R\in\mathbb{R}^{3\times3}$为一旋转矩阵， $r_1,r_2,r_3\in\mathbb{R}^3$，为 $R$的列向量，列向量相互正交：
$$r_i^Tr_j=\{\begin{aligned}0, if i\neq j \\ 1, if i=j\end{aligned}$$
$R$为正交矩阵，$R^TR=RR^T=I$， $\det R=r_1^T(r_2\times r_3)=1$。
所有满足上述性质的 $3\times3$矩阵的集合记为 $SO(3)$， $SO$是special orthogonal的简写。
将 $\mathbb{R}^{n\times n}$中的旋转矩阵定义为：
$$SO(n)=\{R\in\mathbb{R}^{n\times n}: RR^T=I,\det R=+1\}$$ .
我们主要对 $n=3$的情况感兴趣。
$SO(3)\subset\mathbb{R}^{3\times3}$是矩阵相乘操作下的群，对于一个集合 $G$被称为群，如果定义在其元素之上的二值操作$\circ$满足以下条件：
1、运算封闭：若 $g_1,g_2\in G$，则 $g_1\circ g_2\in G$.
2、单位性：对于所有 $g\in G$，存在一个单位元素 $e$，使得$g\circ e=e\circ g$.
3、可逆性：对于任意 $g\in G$存在唯一一个逆 $g^{-1}\in G$，使得 $g\circ g^{-1}=g^{-1}\circ g=e$.
4、结合律：如果 $g_1,g_2,g_3\in G$，则 $(g_1\circ g_2)\circ g_3=g_1\circ(g_2\circ g_3)$
对于 $SO(3)$，注意到：
1、若 $R_1,R_2\in SO(3)$，则有 $R_1R_2\in SO(3)$，因为
$$R_1R_2(R_1R_2)^T=R_1R_2R_2^TR_1^T=I$$
$$\det(R_1R_2)=\det(R_1)\det(R_2)=+1$$
2、单位矩阵为其单位元素.
3、 $R$的逆$R^T\in SO(3)$.
4、矩阵相乘满足群操作的结合律，即 $(R_1R_2)R_3=R_1(R_2R_3)$.
因此， $SO(3)$为一个群，以单位阵为单位元素，矩阵相乘为群操作子，将 $SO(3)$作为 $\mathbb{R}^3$的旋转群。
任何一个绕固定坐标系旋转的刚体都有唯一一个 $R\in SO(3)$与之对应，旋转群 $SO(3)$为系统的配置空间，系统的轨迹为一曲线 $R(t)\in SO(3)， t\in [0,T]$，对于一个系统，如果所有元素 $x\in Q$均对应于一个有效的系统配置，而且系统的每一个配置可以用Q中的唯一元素表示，则称Q为系统的配置空间。
旋转矩阵 $R\in SO(3)$也可以用于坐标变换，将一个点的坐标从一个坐标系变换到另外一个坐标系。如图1中的点q，令 $q_b=[x_b,y_b,z_b]$为q在B下的坐标，相对于A的坐标可以通过下式计算：
$$q_a=x_{ab}x_b+y_{ab}y_b+z_{ab}z_b$$
即：
$q_a=R_{ab}q_b$
换而言之， $R_{ab}$可以看做是 $\mathbb{R}^3$到 $\mathbb{R}^3$的映射，将B中的点旋转至A。