悬挂的绳子,它的函数方程是什么样子的?
参考资料:
前言
一个偶然的机会,笔者记起来,当时的高中数学教材引入自然常数 e e e 的时候,似乎提到一句话,大体意思是说 e e e 在生活中随处可见,比如两段电线杆之间自然下垂的电线就藏着自然常数的身影。
本人虽然没有学过大学物理,但是名义上来说也是学过了《微积分》和《线性代数》,因此机缘巧合之下,就想要试试能不能尽力去推导一下,悬挂的绳子究竟对应着怎样的函数方程,是否有一些美妙的性质。
一开始,笔者尝试通过互联网检索关键词“悬挂的绳子”查找相关资料,果然找到了“悬链线方程”这一比较正式的说法,下面是笔者整理的过程。
定义和假设
这里我们考虑一根长度为 l l l 的绳,假设这根绳子是不可伸缩的,处处密度相等(假设线密度为 ρ \rho ρ )的,柔软的,左右两端点被固定在水平距离为 x x x 的两个端点上。
接下来,我们建立坐标系,设这个函数为
f
(
x
)
f(x)
f(x)(这里的纵坐标并未定义,我们先不做讨论)。根据问题的对称性,该函数图像应该是左右对称的,也就是说,这是一个偶函数,我们重点关注
x
>
0
x>0
x>0 的部分。
(图中只是给出函数的大体图像方便想象,请忽略具体值)
推导
根据假设,该函数的定义域是
x
∈
[
0
,
s
2
]
x \in [0, \frac s 2]
x∈[0,2s], 我们这里选取这样一段绳子,横坐标为
[
0
,
x
1
]
[0, x_1]
[0,x1](
x
1
x_1
x1可以取任意值)。
我们对这一部分绳子进行受力分析,这段绳子受到水平向左的拉力
F
0
F_0
F0,受到斜向右上的拉力
F
1
F_1
F1,设拉力方向与向右水平的夹角角度为
θ
\theta
θ,受到向下的重力
G
G
G。
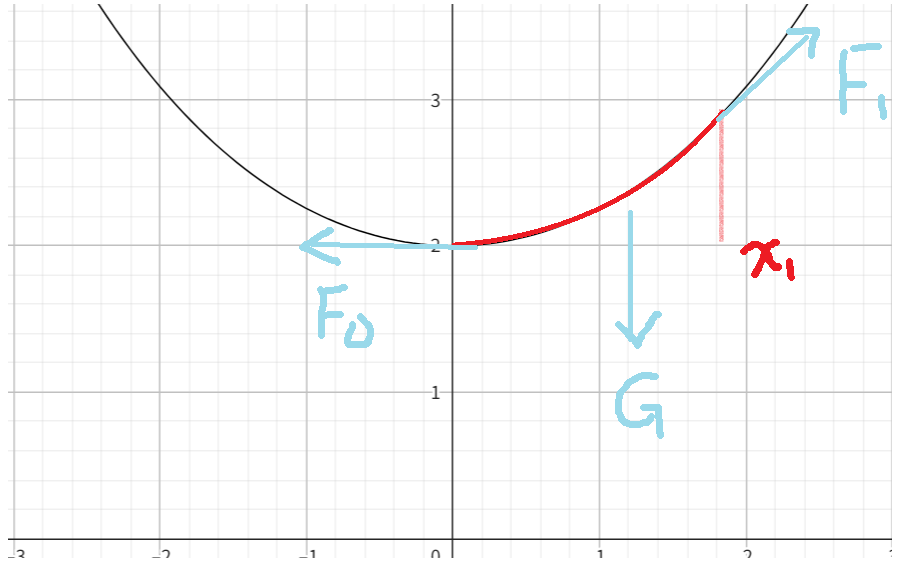
(首先,我们要确定,绳子内部某一点所受拉力的方向一定沿着此处绳子的切线方向):
针对
F
0
F_0
F0,水平的原因是
(
x
=
0
)
(x=0)
(x=0) 处的斜率为0(偶函数/最低点);
针对
F
1
F_1
F1,这里函数的斜率就是
f
′
(
x
1
)
f'(x_1)
f′(x1),力的大小暂时未知;
针对
G
G
G,我们可以用
f
(
x
)
f(x)
f(x) 表示出来这段绳子的长度,从而求出绳子的重力:
G
=
ρ
g
∫
0
x
1
1
+
f
′
2
(
x
)
d
x
G = \rho g \int_{0}^{x_1} \sqrt{1 + f'^2(x)} \,dx
G=ρg∫0x11+f′2(x)dx
下面,我们根据三个力的受力平衡,给出下面两个方程:
F
0
=
F
1
⋅
cos
θ
(
水平方向
)
G
=
F
1
⋅
sin
θ
(
竖直方向
)
F_0 = F_1 \cdot \cos \theta \qquad(水平方向) \\ G = F_1 \cdot \sin \theta \qquad (竖直方向) \\
F0=F1⋅cosθ(水平方向)G=F1⋅sinθ(竖直方向)
两个式子做差:
G
=
F
0
⋅
tan
θ
⇒
ρ
g
∫
0
x
1
1
+
f
′
2
(
x
)
d
x
=
F
0
f
′
(
x
)
(
tan
θ
=
k
=
f
′
(
x
)
)
⇒
ρ
g
F
0
1
+
f
′
2
(
x
)
=
f
′
′
(
x
)
(
两边同时求导消去积分
)
G = F_0 \cdot \tan \theta \\ \Rightarrow \rho g \int_{0}^{x_1} \sqrt{1 + f'^2(x)} \,dx = F_0 f'(x) \qquad(\tan\theta = k = f'(x)) \\ \Rightarrow \frac{\rho g}{F_0}\sqrt{1 + f'^2(x)} = f''(x) \qquad(两边同时求导消去积分)
G=F0⋅tanθ⇒ρg∫0x11+f′2(x)dx=F0f′(x)(tanθ=k=f′(x))⇒F0ρg1+f′2(x)=f′′(x)(两边同时求导消去积分)
为了方便表示,这里的系数是定值,不妨设为
a
a
a,于是有:
a
1
+
f
′
2
(
x
)
=
f
′
′
(
x
)
a \sqrt{1 + f'^2(x)} = f''(x)
a1+f′2(x)=f′′(x)
原本的问题就变成了对这样一个微分方程的求解。
求解微分方程
(过程有些繁琐但是用到的都是比较基础的微积分知识)
这里我直接求助了 deepseek,最后与视频给出的答案也是一致的,过程如下:
令
f
′
(
x
)
=
p
(
x
)
,
f
′
′
(
x
)
=
p
′
(
x
)
,原本的问题变为
p
′
(
x
)
=
p
2
(
x
)
+
1
⇒
d
p
p
2
(
x
)
+
1
=
a
d
x
⇒
d
(
ln
(
p
+
1
+
p
2
)
)
=
a
d
x
⇒
ln
(
p
+
1
+
p
2
)
=
a
x
+
C
这里带入
(
x
=
0
)
的情况,右侧为
C
,左侧因为
p
(
0
)
=
f
′
(
0
)
=
0
,因此
C
=
0
可以确定
于是现在只需要再去求
p
即可。
p
+
1
+
p
2
=
e
a
x
(
1
)
(
这里
(
2
)
的由来比较巧妙,可以理解为
(
1
)
取倒数之后的分子有理化
)
−
p
+
1
+
p
2
=
e
−
a
x
(
2
)
两者联立,就可以得到:
f
′
(
x
)
=
p
=
1
2
(
e
a
x
−
e
−
a
x
)
f
(
x
)
=
1
2
a
(
e
a
x
+
e
−
a
x
)
+
C
这里就回到我们一开始说的纵坐标问题,我们不妨让
C
=
0
,就可以得到一个非常优美的函数!!
f
(
x
)
=
1
2
a
(
e
a
x
+
e
−
a
x
)
令f'(x) = p(x), f''(x) = p'(x),原本的问题变为 \\ p'(x) = \sqrt {p^2(x) + 1} \\ \Rightarrow \frac {dp} {\sqrt {p^2(x) + 1}} = adx \\ \Rightarrow d(\ln (p + \sqrt{1+p^2})) = adx \\ \Rightarrow \ln (p + \sqrt{1+p^2}) = ax + C \\ 这里带入 (x=0)的情况,右侧为C,左侧因为 p(0) = f'(0) = 0,因此C=0可以确定 \\ 于是现在只需要再去求p即可。 \\ p + \sqrt{1+p^2} = e^{ax} \quad (1) \\ (这里(2)的由来比较巧妙,可以理解为(1)取倒数之后的分子有理化)\\ -p + \sqrt{1+p^2} = e^{-ax} \quad (2) \\ 两者联立,就可以得到: \\ f'(x) = p = \frac 1 {2} (e^{ax} - e^{-ax}) \\ f(x) = \frac{1}{2a} (e^{ax} + e^{-ax}) + C \\ 这里就回到我们一开始说的纵坐标问题,我们不妨让 C = 0,就可以得到一个非常优美的函数!!\\ f(x) = \frac{1}{2a} (e^{ax} + e^{-ax})
令f′(x)=p(x),f′′(x)=p′(x),原本的问题变为p′(x)=p2(x)+1⇒p2(x)+1dp=adx⇒d(ln(p+1+p2))=adx⇒ln(p+1+p2)=ax+C这里带入(x=0)的情况,右侧为C,左侧因为p(0)=f′(0)=0,因此C=0可以确定于是现在只需要再去求p即可。p+1+p2=eax(1)(这里(2)的由来比较巧妙,可以理解为(1)取倒数之后的分子有理化)−p+1+p2=e−ax(2)两者联立,就可以得到:f′(x)=p=21(eax−e−ax)f(x)=2a1(eax+e−ax)+C这里就回到我们一开始说的纵坐标问题,我们不妨让C=0,就可以得到一个非常优美的函数!!f(x)=2a1(eax+e−ax)
























 13
13

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








