前言
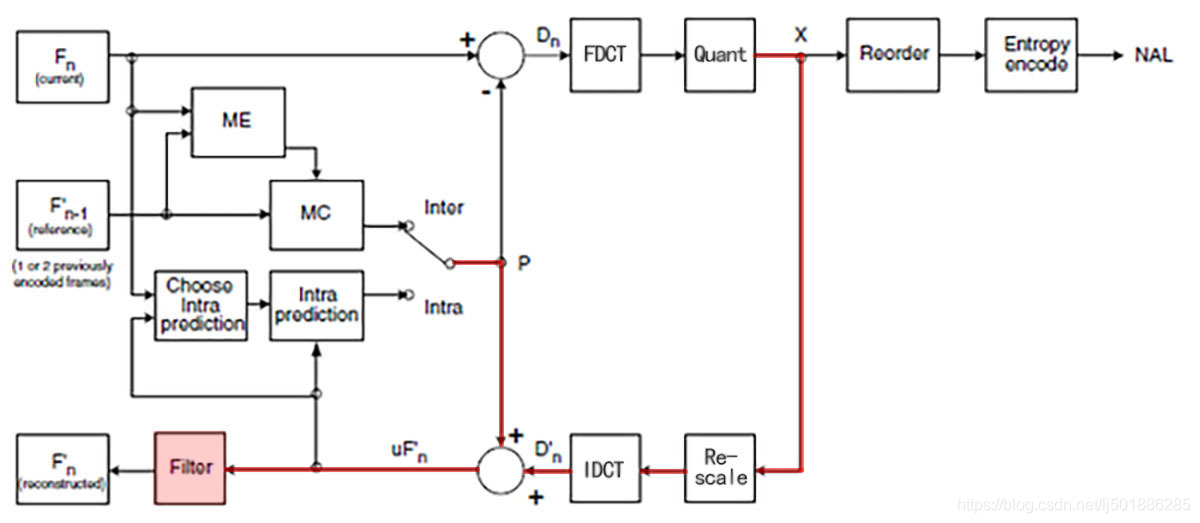
由于FDCT变换后的量化(Quant)过程是一个有损(lossy)过程,会照成信息损失。再经过反量化(Rescale)和IDCT后恢复的矩阵与原矩阵存在一定的误差,特别宏块的边界,会照常恢复的图像呈现方块化,而方块化的图片对于后面的图片预测存在极大的影响,所以我们需要通过环路滤波进行去方块化

真假边界

真边界
即原图像所存在的纹理细节。例如上图foreman的脸部边界
假边界
即原图像平坦区域由于量化操作而导致块边界失真,相邻块之间过度不平滑,呈现出来的边界。例如上图白色块之间的边界
判定
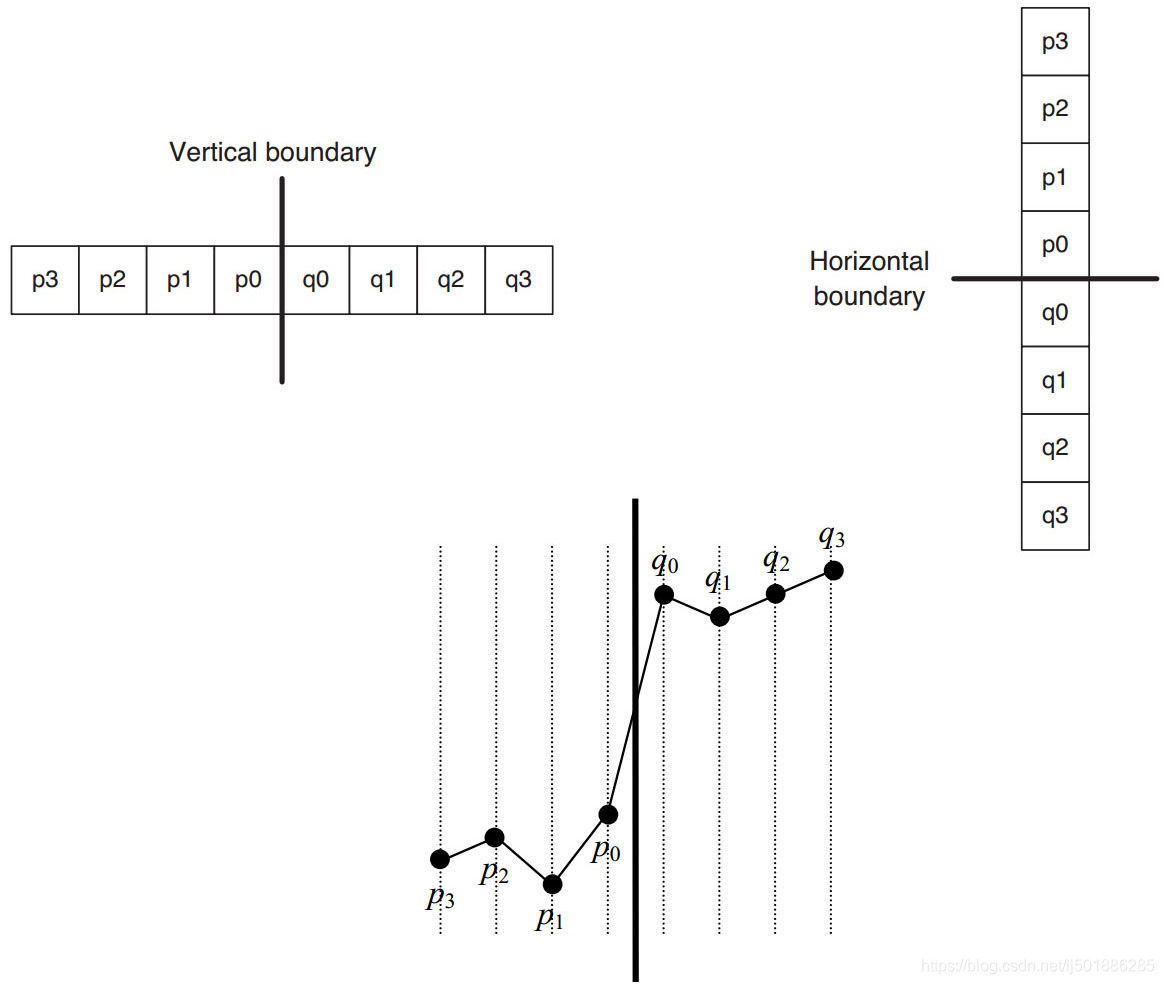
当且仅当以下三个条件满足时才进行滤波
- ∣ p 0 − q 0 ∣ < α ( i n d e x A ) |p_0-q_0|<\alpha(index_A) ∣p0−q0∣<α(indexA)
- ∣ p 1 − p 0 ∣ < β ( i n d e x B ) |p_1-p_0|<\beta(index_B) ∣p1−p0∣<β(indexB)
- ∣ q 1 − q 0 ∣ < β ( i n d e x B ) |q_1-q_0|<\beta(index_B) ∣q1−q0∣<β(indexB)
其中

QP为量化中的参数,范围[0,51],offset给编码器提供一个控制滤波器性能的偏移量,然后我们针对
α
(
i
n
d
e
x
A
)
\alpha(index_A)
α(indexA)和
β
(
i
n
d
e
x
B
)
\beta(index_B)
β(indexB)查表:
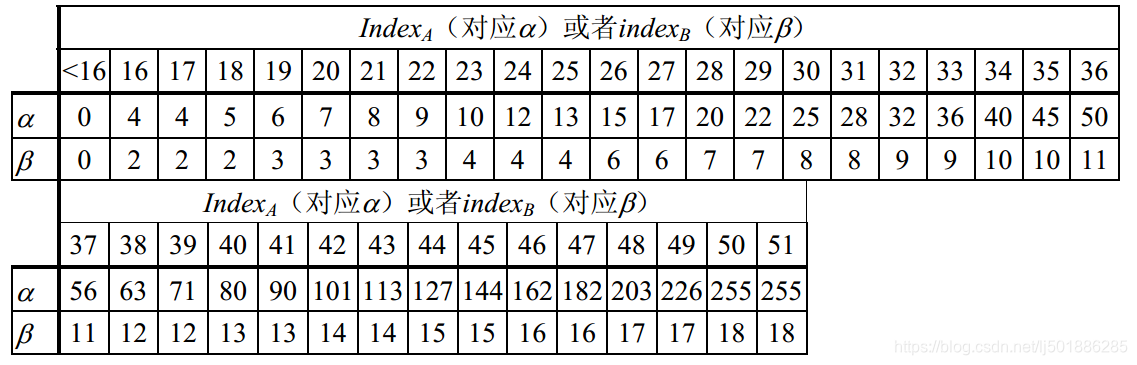
滤波过程
滤波强度Bs

Bs=4时,强度最大;Bs=0时,无需进行滤波。色度块的滤波强度同亮度块
我们所希望的是:
针对平坦区域(低频),使用较强的滤波强度
针对细节区域(高频),使用较弱的滤波强度
滤波顺序

依照从左至右,依上而下的顺序,即
- 16x16的亮度块:a b c d e f g h
- 8x8色度块:i j k l
当Bs = {1,2,3}时
- 更新
p
0
p_0
p0和
q
0
q_0
q0
Δ 0 = ( ( q 0 − p 0 ) < < 2 + ( p 1 − q 1 ) + 4 ) > > 3 p 0 ′ = p 0 + Δ 0 q 0 ′ = q 0 − Δ 0 \Delta_0=( (q_0-p_0) << 2 + (p_1 - q_1) + 4) >> 3\\ p_0'=p_0+\Delta_0\\ q_0'=q_0-\Delta_0 Δ0=((q0−p0)<<2+(p1−q1)+4)>>3p0′=p0+Δ0q0′=q0−Δ0 - 对
p
0
p_0
p0和
q
0
q_0
q0进行限幅
即将 p 0 p_0 p0和 q 0 q_0 q0限制在范围 [ − c 0 , c 0 ] [-c_0,c_0] [−c0,c0]内。 c 0 c_0 c0取值为 c 1 c_1 c1,若同时满足 ∣ p 2 − p 0 ∣ < β ( i n d e x B ) |p_2-p_0|<\beta(index_B) ∣p2−p0∣<β(indexB)和 ∣ q 2 − q 0 ∣ < β ( i n d e x B ) |q_2-q_0|<\beta(index_B) ∣q2−q0∣<β(indexB),则 c 0 = c 1 + 1 c_0=c_1+1 c0=c1+1
若满足 ∣ p 2 − p 0 ∣ < β ( i n d e x B ) |p_2-p_0|<\beta(index_B) ∣p2−p0∣<β(indexB),则
- 更新
p
1
p1
p1
Δ p 1 = ( p 2 + ( p 0 + q 0 + 1 ) > > 1 − 2 p 1 ) > > 1 p 1 ′ = p 1 + Δ p 1 \Delta_{p1}=( p_2 + (p_0+q_0+1)>>1-2p_1 ) >> 1\\ p_1'=p_1+\Delta_{p1}\\ Δp1=(p2+(p0+q0+1)>>1−2p1)>>1p1′=p1+Δp1 - 对
p
1
p1
p1限幅
将 p 1 p1 p1限定在范围 [ − c 1 , c 1 ] [-c_1,c_1] [−c1,c1],其中 c 1 c_1 c1的值查表所得
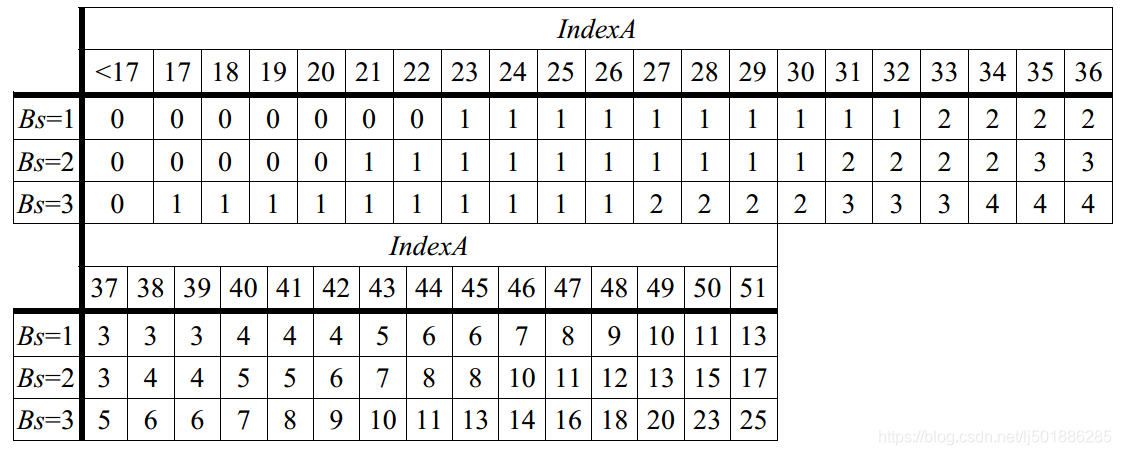
同样的,若满足 ∣ q 2 − q 0 ∣ < β ( i n d e x B ) |q_2-q_0|<\beta(index_B) ∣q2−q0∣<β(indexB),则
- 更新
q
1
q1
q1
Δ q 1 = ( q 2 + ( q 0 + p 0 + 1 ) > > 1 − 2 q 1 ) > > 1 q 1 ′ = q 1 + Δ q 1 \Delta_{q1}=( q_2 + (q_0+p_0+1)>>1-2q_1 ) >> 1\\ q_1'=q_1+\Delta_{q1}\\ Δq1=(q2+(q0+p0+1)>>1−2q1)>>1q1′=q1+Δq1 - 对
q
1
q1
q1限幅
限幅规则同 p 1 p1 p1
当Bs = 4时
- 更新
p
0
p_0
p0和
q
0
q_0
q0
· 若 ∣ p 0 − q 0 ∣ < α > > 2 + 2 |p_0-q_0|<\alpha>>2+2 ∣p0−q0∣<α>>2+2时
p 0 ′ = ( p 2 + 2 p 1 + 2 p 0 + 2 q 0 + q 1 + 4 ) > > 3 q 0 ′ = ( q 2 + 2 q 1 + 2 q 0 + 2 p 0 + p 1 + 4 ) > > 3 p_0'=(p_2+2p_1+2p_0+2q_0+q_1+4)>>3\\ q_0'=(q_2+2q_1+2q_0+2p_0+p_1+4)>>3 p0′=(p2+2p1+2p0+2q0+q1+4)>>3q0′=(q2+2q1+2q0+2p0+p1+4)>>3
· 否则
p 0 ′ = ( 2 p 1 + p 0 + q 1 + 2 ) > > 2 q 0 ′ = ( 2 q 1 + q 0 + p 1 + 2 ) > > 2 p_0'=(2p_1+p_0+q_1+2)>>2\\ q_0'=(2q_1+q_0+p_1+2)>>2 p0′=(2p1+p0+q1+2)>>2q0′=(2q1+q0+p1+2)>>2 - 若满足
∣
p
2
−
p
0
∣
<
β
(
i
n
d
e
x
B
)
|p_2-p_0|<\beta(index_B)
∣p2−p0∣<β(indexB),则更新
p
1
p_1
p1和
p
2
p_2
p2
p 1 ′ = ( p 2 + p 1 + p 0 + q 0 + 2 ) > > 2 p 2 ′ = ( 2 p 3 + 3 p 2 + p 1 + p 0 + q 0 + 4 ) > > 3 p_1'=(p_2+p_1+p_0+q_0+2)>>2\\ p_2'=(2p_3+3p_2+p_1+p_0+q_0+4)>>3 p1′=(p2+p1+p0+q0+2)>>2p2′=(2p3+3p2+p1+p0+q0+4)>>3 - 若满足
∣
q
2
−
q
0
∣
<
β
(
i
n
d
e
x
B
)
|q_2-q_0|<\beta(index_B)
∣q2−q0∣<β(indexB),则更新
q
1
q_1
q1和
q
2
q_2
q2
q 1 ′ = ( q 2 + q 1 + q 0 + q 0 + 2 ) > > 2 q 2 ′ = ( 2 q 3 + 3 q 2 + q 1 + q 0 + p 0 + 4 ) > > 3 q_1'=(q_2+q_1+q_0+q_0+2)>>2\\ q_2'=(2q_3+3q_2+q_1+q_0+p_0+4)>>3 q1′=(q2+q1+q0+q0+2)>>2q2′=(2q3+3q2+q1+q0+p0+4)>>3



























 1028
1028

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








