梯度下降之随机梯度下降，牛顿迭代，动量法

我不是阿呆啊

于 2024-04-08 10:52:29 发布

阅读量971

点赞数 14

分类专栏：机器学习文章标签： python numpy 机器学习线性回归

本文链接：https://blog.csdn.net/lml3040891085/article/details/137495756

版权

机器学习专栏收录该内容

1 篇文章 0 订阅

订阅专栏

本文详细介绍了经典梯度下降、随机梯度下降、牛顿迭代法和动量法等优化算法，通过代码示例展示了它们在求解线性回归问题上的应用，以及各自的优缺点。

摘要由CSDN通过智能技术生成

一.start

在这个充满数学魔法和编程魅力的时代，我怀着一颗充满好奇心的心情，来与大家分享一些我所研究的梯度下降算法。不过，在我开始之前，我必须要坦诚地承认，梯度下降听起来像是一场令人头痛的滑行之旅，但请放心，我会尽力让这趟旅程变得轻松愉快，就像在数学乐园中游玩一样。Ok,一起来看看吧。

二.main

1.经典梯度下降

首先，让我们来谈谈经典梯度下降算法。这就像是我们在寻找最佳路线时所采取的一种策略：一步一步地沿着山坡走，直到我们找到了山脚下的谷底。虽然有时候可能会遇到一些坑坑洼洼，但我们总能找到最佳的下降方向，来逐渐接近最优解。

优点：简单易懂，易于实现。在小规模问题上表现良好，收敛性较好。
局限性：可能会受到局部极值的困扰，在高维空间中收敛速度较慢。

import numpy as np
import matplotlib.pyplot as plt
def main(epoch=1000,w=(np.random.randint(0,1,(1,2))+0.1)[0],root='./data'):
    #数据的读取
    f = open(root, 'r')
    x = list(map(float, f.readline().split()))
    y = list(map(float, f.readline().split()))
    f.close()
    #归一化
    x=[(i-min(x))/(max(x)-min(x)) for i in x]
    y=[(i-min(y))/(max(y)-min(y)) for i in y]
    length = len(x)
    X=np.array(x)
    Y=np.array(y)
    print(w)#打印初始参数
    I=[1 for i in range(len(X))]#方便将y=ax+b的b一起进行矢量化编程
    steps=0.01#学习率
    def MSE(w):#损失函数
        MSE=np.dot((np.dot(w, np.array([X, I])) - np.array(Y)), (np.dot(w, np.array([X, I])) - np.array(Y)).T) / length#np.dot((np.dot(w,np.array([X,I]))-Y),(np.dot(w,np.array([X,I]))-Y).T)/len(x)
        return MSE
    def graint(w):#计算梯度
        g=np.dot(np.dot(w,np.array([X,I]))-Y,np.array([X,I]).T)*steps
        print(g)
        w-=g
        return w
    width_epch = 5  # 对于epoch的宽度
    width_MSE = 20  # 对于MSE的宽度，确保有足够的空间显示浮点数
    width_w = 20  # 对于w的宽度，根据w的长度和内容调整
    loss=[]
    for i in range(1,epoch+1):
        loss.append(MSE(w))
        #print(f"epoch={i}   MSE={MSE(w)}   w={w}")
        w_str = ', '.join(map(str, w))  # 将数组或列表转换为字符串，用逗号分隔
        print(f"epch={i:<{width_epch}}   MSE={MSE(w):<{width_MSE}}   w={w_str:<{width_w}}")
        w=graint(w)
    print(f"result: {w},loss={loss[-1]}")
    plt.subplot(1,2,1)
    plt.scatter(X,Y,color='g')
    plt.plot(X,np.dot(w,np.array([X,I])),'r')
    plt.subplot(1,2,2)
    plt.plot([i for i in range(epoch)],loss,color='r')
    plt.show()
    return loss
if __name__=="__main__":
    main(500)

2.随机梯度下降

接下来，让我们进入随机梯度下降算法的世界。这就像是在山脚下寻找宝藏的过程：我们可能会走得有些冒险，但每一步都可能带来意想不到的惊喜。有时候我们可能会踩到一些石头，但正是这些挑战，让我们变得更加灵活，更加适应各种情况。

优点：计算速度快，适用于大规模数据和高维空间。容易跳出局部极值点，有一定的随机性，有助于避免陷入局部最优解。
局限性：收敛性不稳定，可能会出现震荡现象。对数据的预处理要求较高，需要进行归一化或标准化处理。

import random

import numpy as np
import matplotlib.pyplot as plt

def main(times=100,w=np.random.randint(0,1,(1,2))+0.1,root='./data',batch_size):
    f=open(root,'r')
    data_x=list(map(float,f.readline().split()))#[1.1,2.7,3.5,3.6,4.7,5.1]
    data_y=list(map(float,f.readline().split()))#[1.9,2.3,3.4,2.9,3.4,4.3]
    #归一化
    data_x=[(i - min(data_x)) / (max(data_x)-min(data_x)) for i in data_x]
    data_y=[(i - min(data_y)) / (max(data_y)-min(data_y)) for i in data_y]
    X=np.array(data_x).reshape(-1,1)
    Y=np.array(data_y).reshape(-1,1)
    length=len(X)
    print(w)#打印初始化参数
    A=np.array([[1,0],[0,1]])

    steps=0.1#学习率
    LOSS=[]
    def loss(w):
        I = [1 for i in range(len(X))]
        loss = np.dot((np.dot(w, np.array([data_x, I])) - np.array(data_y)), (np.dot(w, np.array([data_x, I])) - np.array(data_y)).T) / length
        return loss
    def graint(w,x_batch,y_batch):
        I = [1 for i in range(len(x_batch))]
        return np.dot(np.dot(w, np.array([x_batch, I])) - y_batch, np.array([x_batch, I]).T) * steps
    for i in range(1,times+1):
        start=random.randint(0,length-batch_size+1)
        x_batch = X[start:start+batch_size)]
        y_batch = Y[start:start+batch_size]
        grad=graint(w,[i[0] for i in x_batch],[j[0] for j in y_batch])
        Loss=loss(w)
        LOSS.append(Loss[0][0])
        print(f"epoch={i}    loss={round(Loss[0][0],6)}   w={round(w[0][0],6),round(w[0][1],6)}")
        w-=np.array(grad).reshape(1,2)
    print(f"结果w={w},loss={Loss}")
    I=[1 for i in range(len(data_x))]
    y_pre=np.dot(w,np.array([data_x,I]))[0]
    plt.subplot(1,2,1)
    plt.scatter(data_x,data_y,color='g')
    plt.plot(data_x,y_pre,color='r')
    plt.subplot(1,2,2)
    plt.plot([i for i in range(times)],LOSS,color='r')
    plt.show()
    return LOSS
if __name__=="__main__":
    main(1000)

3.牛顿迭代法

然后，我们来谈谈牛顿迭代法。这就像是我们拥有了一辆超级跑车，可以以更快的速度穿越复杂的地形，直奔目的地。牛顿迭代法利用了更多的信息，以更快的速度收敛于最优解，但有时候也会需要更多的计算资源，就像是开超级跑车一样，得确保有足够的油料和维护保养。

优点：收敛速度较快，具有二阶收敛性，对于某些非凸函数也能有效收敛。对于高维问题也能表现良好。
局限性：需要计算目标函数的二阶导数（Hessian矩阵），计算复杂度较高，对于大规模问题不太实用。并且在某些情况下可能会出现矩阵奇异性导致无法收敛的问题。

import random

import numpy as np
import matplotlib.pyplot as plt

def main(times=100,w=np.random.randint(0,1,(1,2))+0.1,root='./data'):
    f=open(root,'r')
    data_x=list(map(float,f.readline().split()))
    data_y=list(map(float,f.readline().split()))
    #归一化
    data_x=[(i - min(data_x)) / (max(data_x)-min(data_x)) for i in data_x]
    data_y=[(i - min(data_y)) / (max(data_y)-min(data_y)) for i in data_y]
    X=np.array(data_x).reshape(-1,1)
    Y=np.array(data_y).reshape(-1,1)
    length=len(X)
    A=np.array([[1,0],[0,1]])
    def loss(w):
        I = [1 for i in range(len(X))]
        loss = np.dot((np.dot(w, np.array([data_x, I])) - np.array(data_y)), (np.dot(w, np.array([data_x, I])) - np.array(data_y)).T) / length
        return loss
    def graint(w,x_batch,y_batch):
        I = [1 for i in range(len(x_batch))]
        return np.dot(np.dot(w, np.array([x_batch, I])) - y_batch, np.array([x_batch, I]).T)
    def Hessian(w,x_batch):
        I = np.array([1 for i in range(len(x_batch))])
        return -2*np.dot(np.array([x_batch,I]),np.array([x_batch,I]).T)
    result=[w,loss(w)[0][0],0]
    LOSS = []
    for i in range(1,times+1):
        start=random.randint(0,length-49)
        x_batch = X[start:start+50]
        y_batch = Y[start:start+50]
        grad=graint(w,[i[0] for i in x_batch],[j[0] for j in y_batch])
        hess=Hessian(w,[i[0] for i in x_batch])
        Loss=loss(w)
        LOSS.append(Loss[0][0])
        print(f"epoch={i}    loss={round(Loss[0][0],6)}   w={round(w[0][0],6),round(w[0][1],6)}")
        steps=np.linalg.solve(hess, -grad.reshape(-1,1))
        w-=steps.reshape(1,2)
        if Loss[0][0]<result[1]:
            result=[w,Loss[0][0],i]
    print(f"结果w={result[0]},loss={result[1]},对应迭代次数{result[2]}")
    I=[1 for i in range(len(data_x))]
    y_pre=np.dot(result[0],np.array([data_x,I]))[0]
    plt.subplot(1,2,1)
    plt.scatter(data_x,data_y,color='g')
    plt.plot(data_x,y_pre,color='r')
    plt.subplot(1,2,2)
    plt.plot([i for i in range(times)],LOSS,color='r')
    plt.show()
    return LOSS
if __name__=="__main__":
    main(50)

4.动量法

最后，让我们来谈谈动量法。这就像是我们在滑雪时所经历的一种体验：我们利用动量来顺利地穿越起伏不平的地形，避免陷入平庸的谷底。动量法让我们能够更快地前进，同时也更加稳定，就像是在滑雪场上保持动态平衡一样。

优点：加入了动量项，有助于加速收敛速度，尤其是在沟壑较多的情况下。能够有效平滑优化路径，减少震荡，增强了算法的稳定性。
局限性：可能会因为动量项的设置不当而导致算法过度“惯性”，使得无法快速收敛。需要进行超参数的调节。

import numpy as np
from matplotlib import pyplot as plt
#丑陋的动量法
def main(epoch=1000,w=np.random.randint(0,1,(1,2))+0.1,root='./data'):
    f=open(root,'r')
    data_x=list(map(float,f.readline().split()))
    data_y=list(map(float,f.readline().split()))
    #归一化
    data_x = [(i - min(data_x)) / (max(data_x) - min(data_x)) for i in data_x]
    data_y = [(i - min(data_y)) / (max(data_y) - min(data_y)) for i in data_y]
    print(w.shape)
    #model=ax+b
    length=len(data_x)
    y=np.array(data_y).reshape(-1,1)
    x=np.array([[i,1.000000] for i in data_x]).reshape(-1,2)
    def get_loss(w):
        loss=np.dot((np.dot(w,x.T).T-y).T,np.dot(w,x.T).T-y)/length
        return loss
    def graint(w,x_batch,y_batch):
        grad=np.dot(x.T,(np.dot(w,x_batch.T).T-y_batch)).T
        return grad

    w=np.array([[0.0,0.0]]).reshape(1,2)
    learn_rate=0.01
    epoch=epoch
    LOSS=[]
    weight=np.array([[1.0,1.0]]).reshape(1,2)
    old_grad=graint(w,x,y)*np.array([[1.0,-1.0]]).reshape(1,2)
    B=0.3#先前累积动量的影响权重
    W=[w[0].tolist()]
    for i in range(1,epoch+1):
        loss=get_loss(w)
        LOSS.append(loss[0][0])
        print(f"epoch={i}    loss={round(loss[0][0],6)}   w={round(w[0][0],20),round(w[0][1],20)}")
        grad=graint(w,x,y)
        weight=(weight*B+(1-B)*np.array([5 if grad[0][i]*old_grad[0][i]>0 else 0.3 for i in range(len(grad[0]))]).reshape(1,2))
        print(weight,np.array([5 if grad[0][i]*old_grad[0][i]>0 else 0.3 for i in range(len(grad[0]))]).reshape(1,2))
        w-=grad*learn_rate*weight
        W.append(w[0].tolist())

    plt.figure('result',(16,6))
    plt.subplot(1,3,1)
    plt.xlabel("x")
    plt.ylabel('y')
    y_pre=np.dot(w,x.T)[0]
    plt.scatter(data_x,data_y,color='g',label='points')
    plt.plot(data_x,y_pre,color='r',label='pred')
    plt.legend()
    plt.subplot(1,3,2)
    plt.plot(range(1,len(LOSS)+1),LOSS,color='r')
    plt.xlabel('epoch')
    plt.ylabel('loss')
    plt.subplot(1,3,3)
    ax2 = plt.subplot2grid((1, 3), (0, 2))
    ax2.set_title("loss_denggaoxian")
    ax2.set_xlabel("a")
    ax2.set_ylabel("b")
    length = 100
    a = np.linspace(w[0][0] - 1, w[0][0] + 1, length)
    b = np.linspace(w[0][1] - 0.5, w[0][1] + 0.5, length)
    Loss = [[0 for i in range(length)] for j in range(length)]
    for i in range(length):
        for j in range(length):
            w = np.array([a[i], b[j]]).reshape(1, 2)
            Loss[i][j] = get_loss(w)[0][0]
    ax2.contourf(a, b, Loss, 20, alpha=0.6, cmap=plt.cm.hot)
    C = ax2.contour(a, b, Loss, 40, colors='black')
    lx = [float(W[j][0]) for j in range(len(W))]
    ly = [float(W[j][1]) for j in range(len(W))]
    plt.plot(lx, ly, color='b', marker='*', linewidth='1', markersize='5')
    plt.clabel(C, inline=True, fontsize=10)
    plt.show()
    return LOSS
if __name__=="__main__":
    main(100)

5.对比分析

import matplotlib.pyplot as plt
import GD
import SGD
import Newton
import Momentum
import numpy as np
epoch=100
w1=np.array([[0.0,0.0]])
loss1=GD.main(epoch,w1[0])
w2=np.array([[0.0,0.0]])
loss2=SGD.main(epoch,w2)
w3=np.array([[0.0,0.0]])
loss3=Newton.main(epoch,w3)
w4=np.array([[0.0,0.0]])
loss4=Momentum.main(epoch,w4)
plt.plot([i for i in range(epoch)],loss1,color='r',label='GD')
plt.plot([i for i in range(epoch)],loss2,color='g',label='SGD')
plt.plot([i for i in range(epoch)],loss3,color='b',label='Newton')
plt.plot([i for i in range(epoch)],loss4,color='orange',label='Momentum')
plt.title("loss change with epoch")
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend()
plt.show()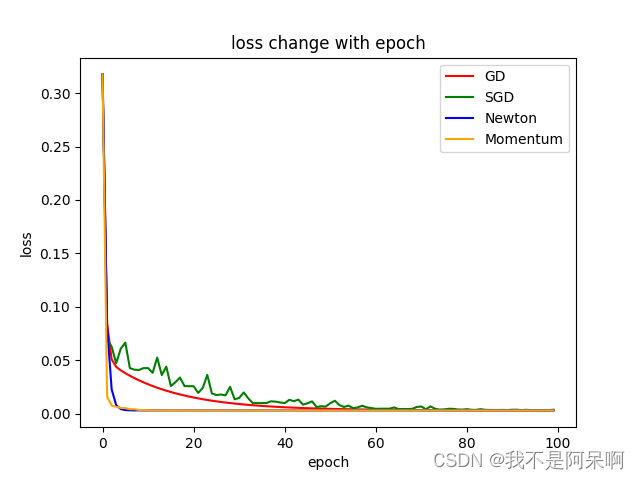

//注意文件路径

三.end

这次梯度下降算法之旅，是我在探索优化世界的过程中的第一次分享，也是我对知识的虚心求教之旅。每一种算法都有其独特的魅力和价值，我也深知自己在这个领域只是初学者，仍然需要不断学习和探索。因此，我诚挚地向各位请教，希望能够从大家的经验和智慧中汲取更多的营养，使自己能够在优化的道路上更进一步。

一为感觉讲的不错的博主

我不是阿呆啊

关注

14
点赞
踩
17

收藏

觉得还不错? 一键收藏
2
评论
梯度下降之随机梯度下降，牛顿迭代，动量法

这次梯度下降算法之旅，是我在探索优化世界的过程中的第一次分享，也是我对知识的虚心求教之旅。因此，我诚挚地向各位请教，希望能够从大家的经验和智慧中汲取更多的营养，使自己能够在优化的道路上更进一步。不过，在我开始之前，我必须要坦诚地承认，梯度下降听起来像是一场令人头痛的滑行之旅，但请放心，我会尽力让这趟旅程变得轻松愉快，就像在数学乐园中游玩一样。牛顿迭代法利用了更多的信息，以更快的速度收敛于最优解，但有时候也会需要更多的计算资源，就像是开超级跑车一样，得确保有足够的油料和维护保养。最后，让我们来谈谈动量法。
复制链接

扫一扫