概述
本篇是“练习项目”系列的第五篇,主要练习程序化生成各种多边形的例子。这一篇博客,主要都是一些数学知识,这里推荐一个软件:GeoGebra。这个软件可以很方便地画出各种函数的几何表示,对于问题的分析很有帮助。
实例
1、圆形
在UV坐标系中,根据给定的圆心和半径,判断当前片元的UV值到圆心的距离是否小于半径。
主要的代码如下:
float Circle(float2 center, float radius, float2 uv)
{
return 1 - step(radius, distance(uv, center));
}
这里对step方法不熟悉的话,可以查一下资料。
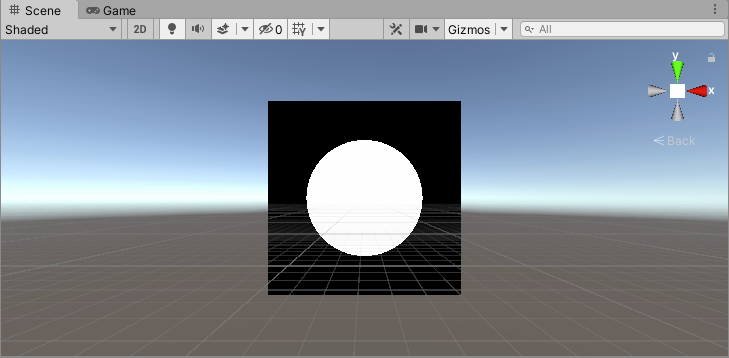
2、柔和的圆形
可以看到,上面白色区域与黑色区域的交界非常尖锐,下面会对边界做柔和操作。
主要的改变,就是不再使用step方法,而是使用smoothstep方法。这样,可以在边界处柔和混合两种颜色。
float SmoothCircle(float2 center, float radius, float smoothWidth, float2 uv)
{
return 1 - smoothstep(radius - smoothWidth, radius, distance(uv, center));
}
对smoothstep方法不熟悉的,可以查一下其它资料。
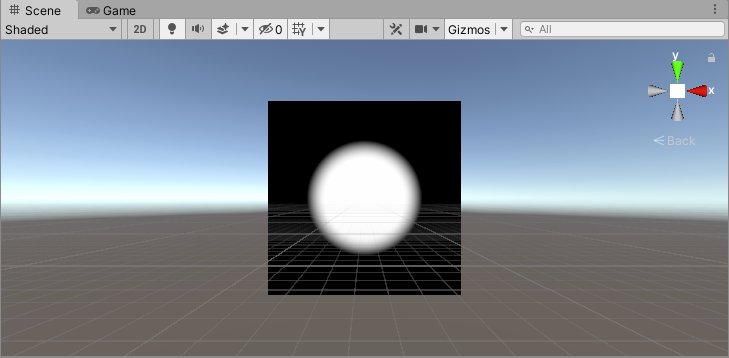
3、多边形
这里比较复杂,需要比较多的运算变换,下面一步步来介绍。注意,这里以三角形为例,其它多边形原理相同。
原始的UV坐标系,U和V的值域为 [ 0 , 1 ] [0,1] [0,1],如下图所示:
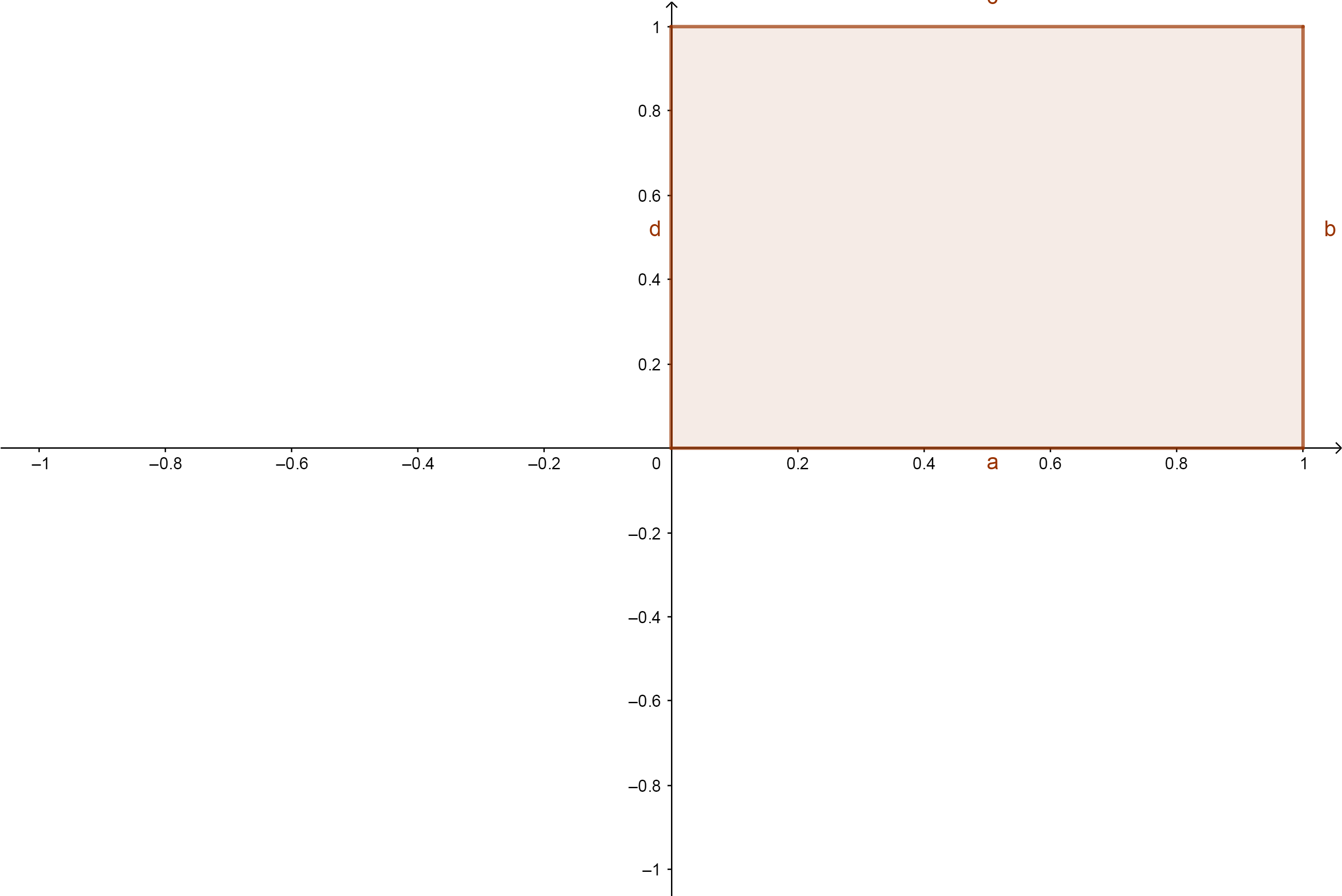
将值域从 [ 0 , 1 ] [0,1] [0,1]变换到 [ − 1 , 1 ] [-1,1] [−1,1]。
input.uv = input.uv * 2 - 1; //[-1, 1],(0,0)在正中心
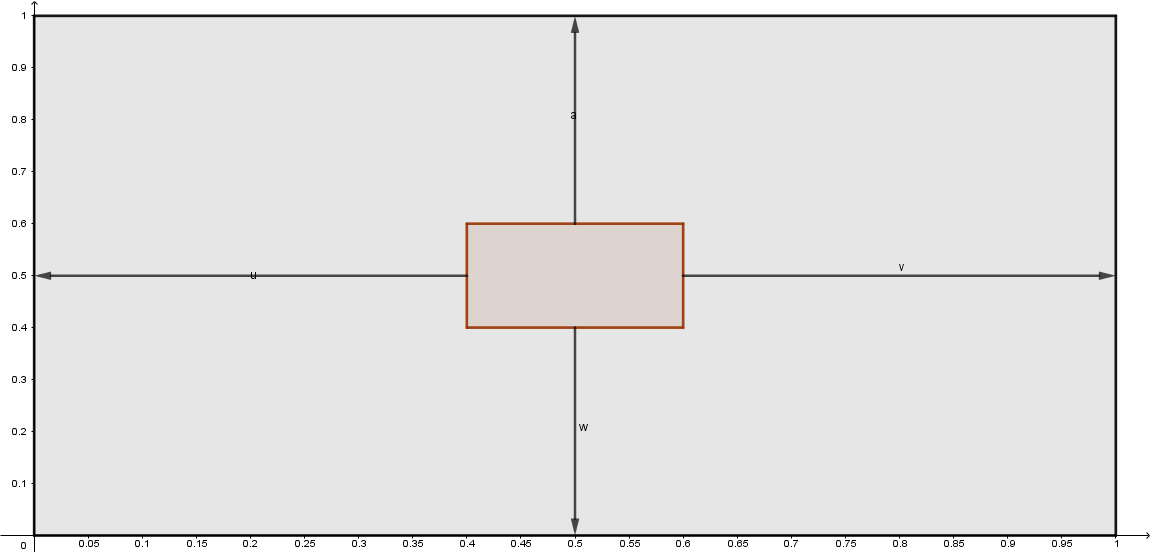
此时,UV坐标系如下图所示:
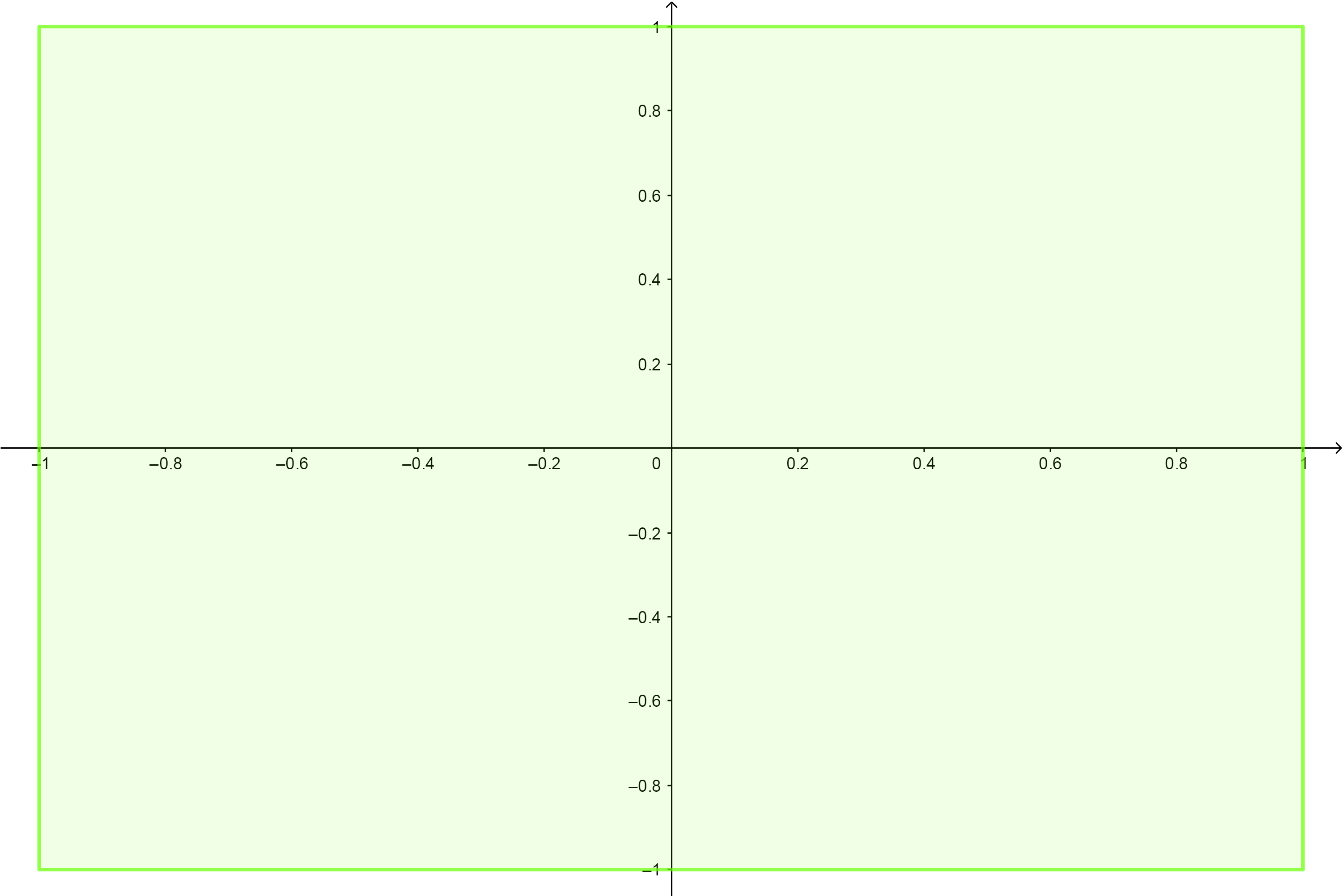
将直角坐标系转化为极坐标系。
float a = atan2(input.uv.y, input.uv.x) + PI; //[0, 2π],将整个界面变成角度分布(极坐标系)
这里要注意 ,atan2函数返回的是原点至点(x,y)的方位角,即与 x 轴的夹角。返回值的单位为弧度,取值范围为 [ − π , π ] [-\pi,\pi] [−π,π]。这里,加上PI是为了把值域转化到 [ 0 , π ] [0,\pi] [0,π]。
对于UV坐标 ( 1 , 1 ) (1,1) (1,1)来说,相当于逆时针旋转 π \pi π弧度,向量 u u u旋转到了向量 v v v。如下图所示:
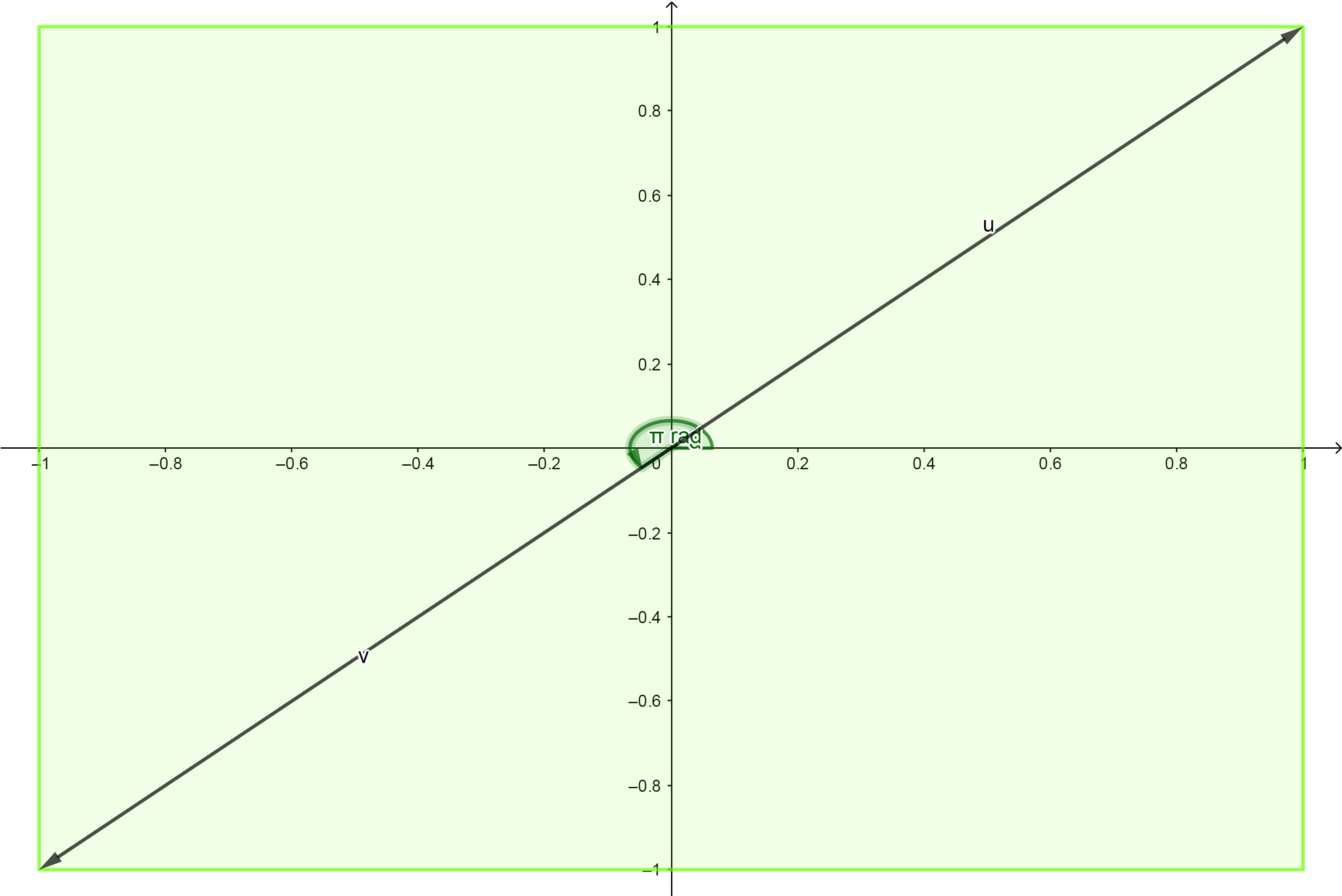
根据多边形的变数,把整个圆周均分,得出每条边对于的弧度。
float r = (2 * PI) / float(_Num); //一条边对应的角度(中心连接边的两个端点)
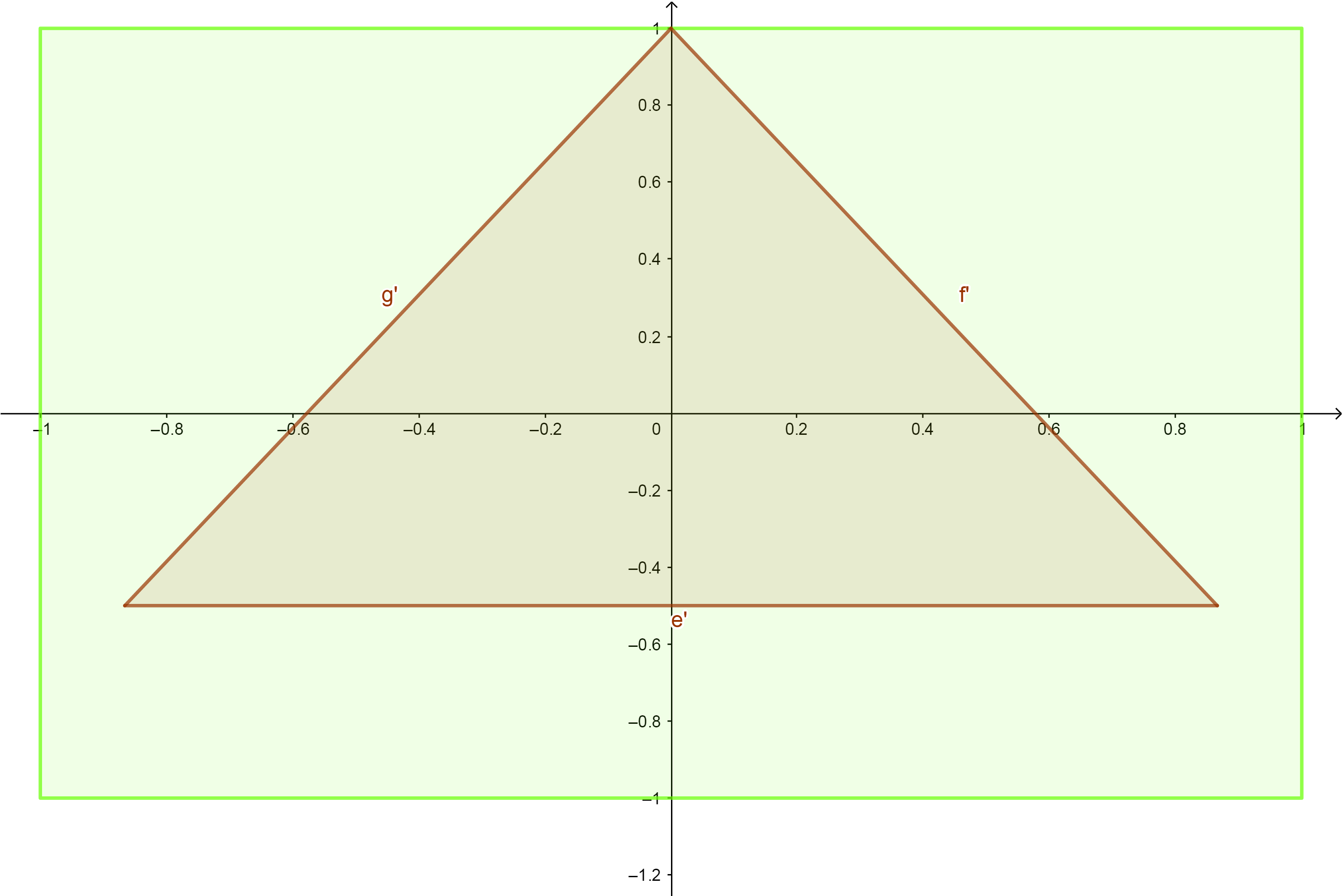
对于三角形,如下所示:
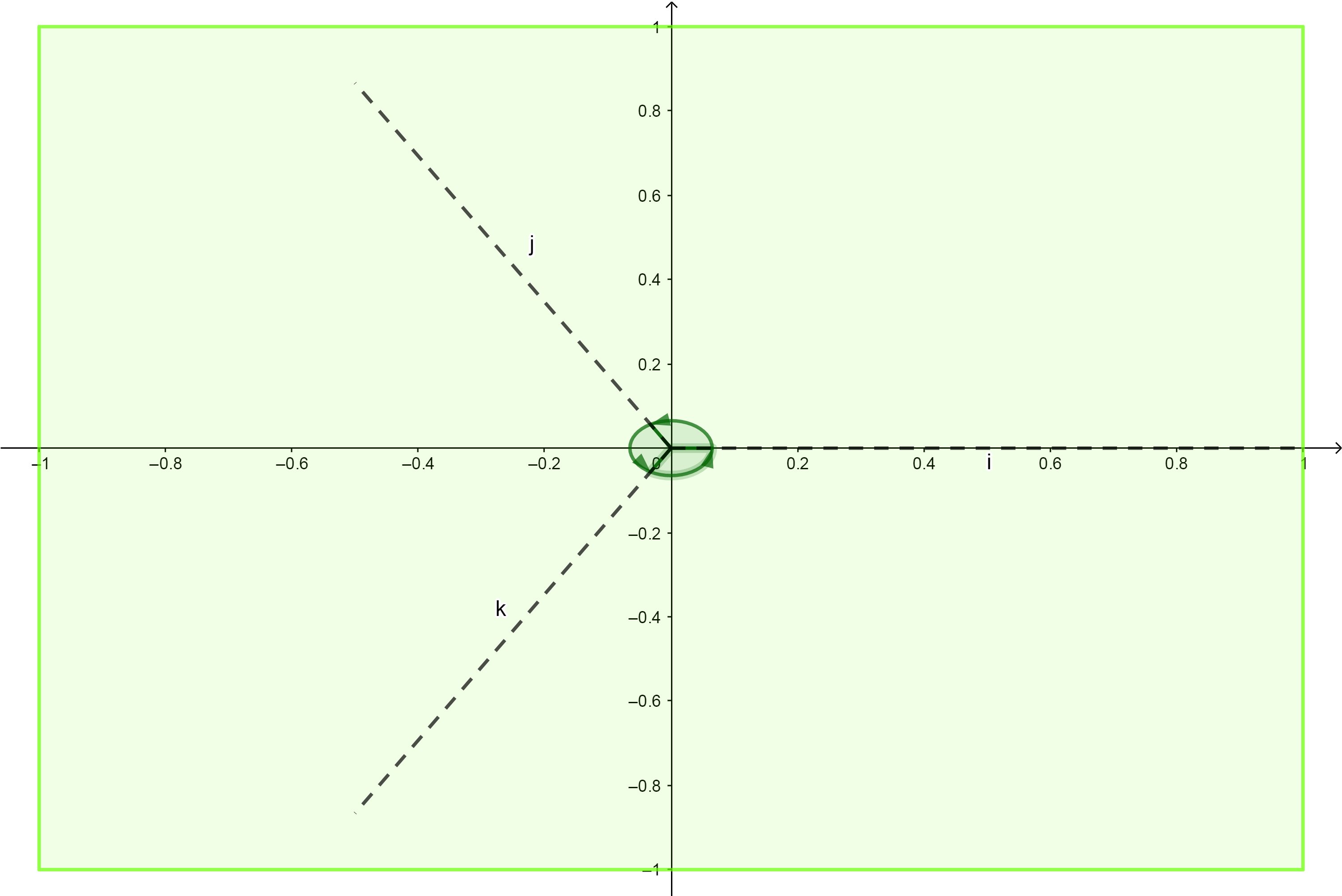
下面,需要计算向量 v v v在最近的一条分界边的投影。
先计算经过了几条边: a / r a/r a/r。
向上取整: f l o o r ( 0.5 + a / r ) floor(0.5 + a/r) floor(0.5+a/r)。
计算经过的几条边的所有弧度: f l o o r ( 0.5 + a / r ) ∗ r floor(0.5 + a/r) * r floor(0.5+a/r)∗r。
计算向量 v v v到最近的一条分界边的弧度: f l o o r ( 0.5 + a / r ) ∗ r − a floor(0.5 + a/r) * r - a floor(0.5+a/r)∗r−a。
计算夹角的余弦值: c o s ( f l o o r ( 0.5 + a / r ) ∗ r − a ) cos(floor(0.5 + a/r) * r - a) cos(floor(0.5+a/r)∗r−a)。
得到向量 v v v在分界边上的投影: c o s ( f l o o r ( 0.5 + a / r ) ∗ r − a ) ∗ l e n g t h ( i n p u t . u v ) cos(floor(0.5 + a/r) * r - a) * length(input.uv) cos(floor(0.5+a/r)∗r−a)∗length(input.uv)。
float d = cos(floor(0.5 + a / r) * r - a) * length(input.uv);
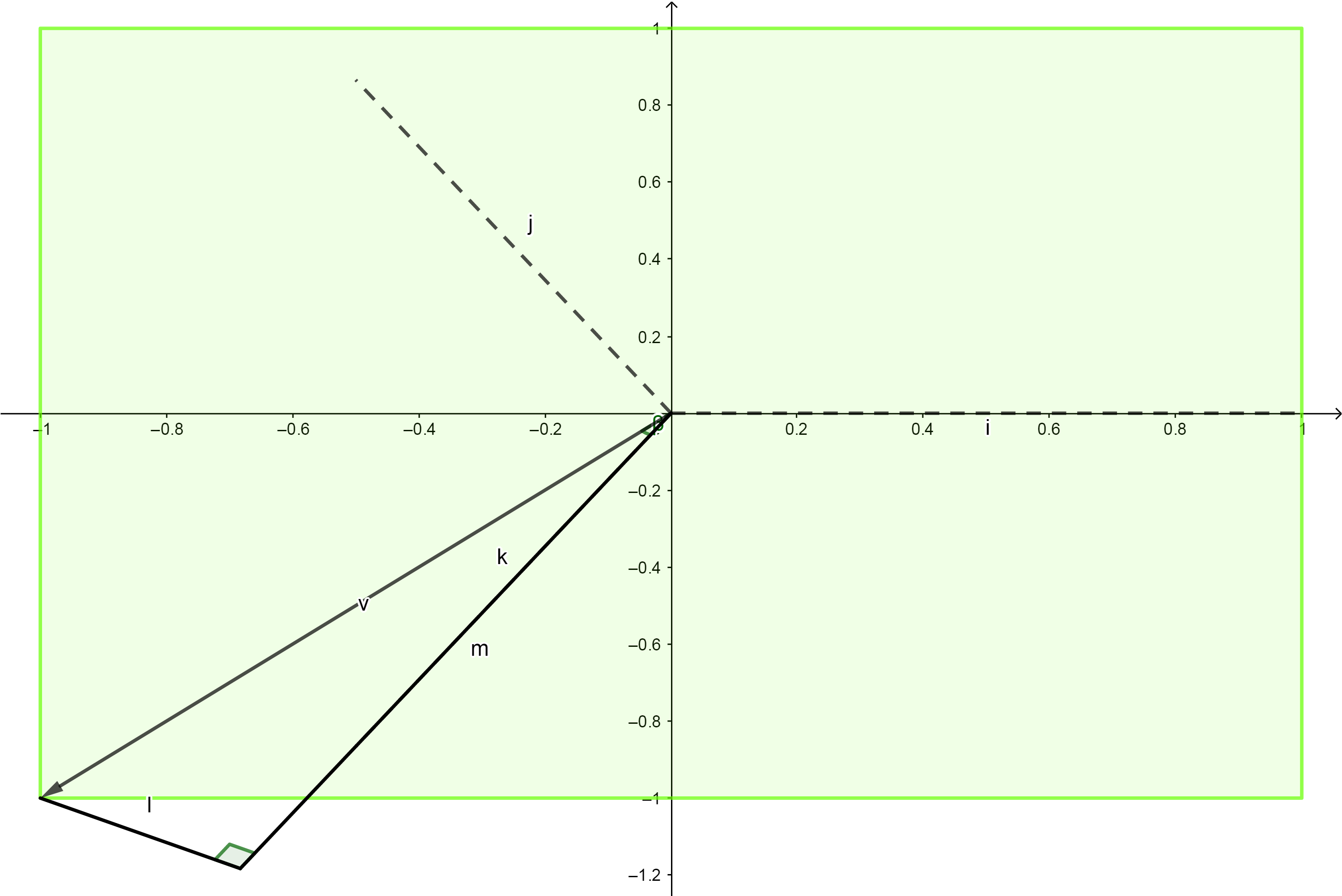
得到投影距离后,与配置的size比较,判断是否在多边形范围内。
half3 col = 1 - step(_Size, d);
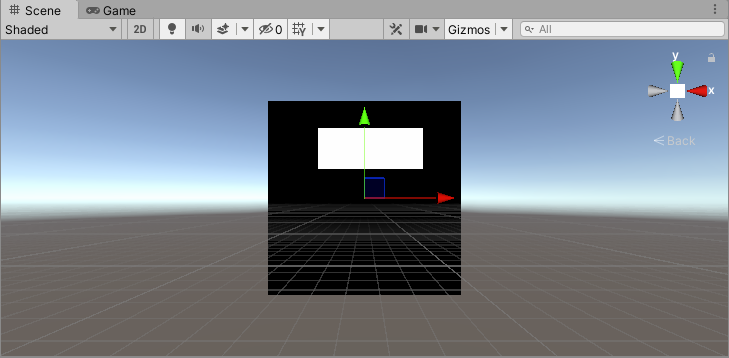
此时,得到的多边形如下:
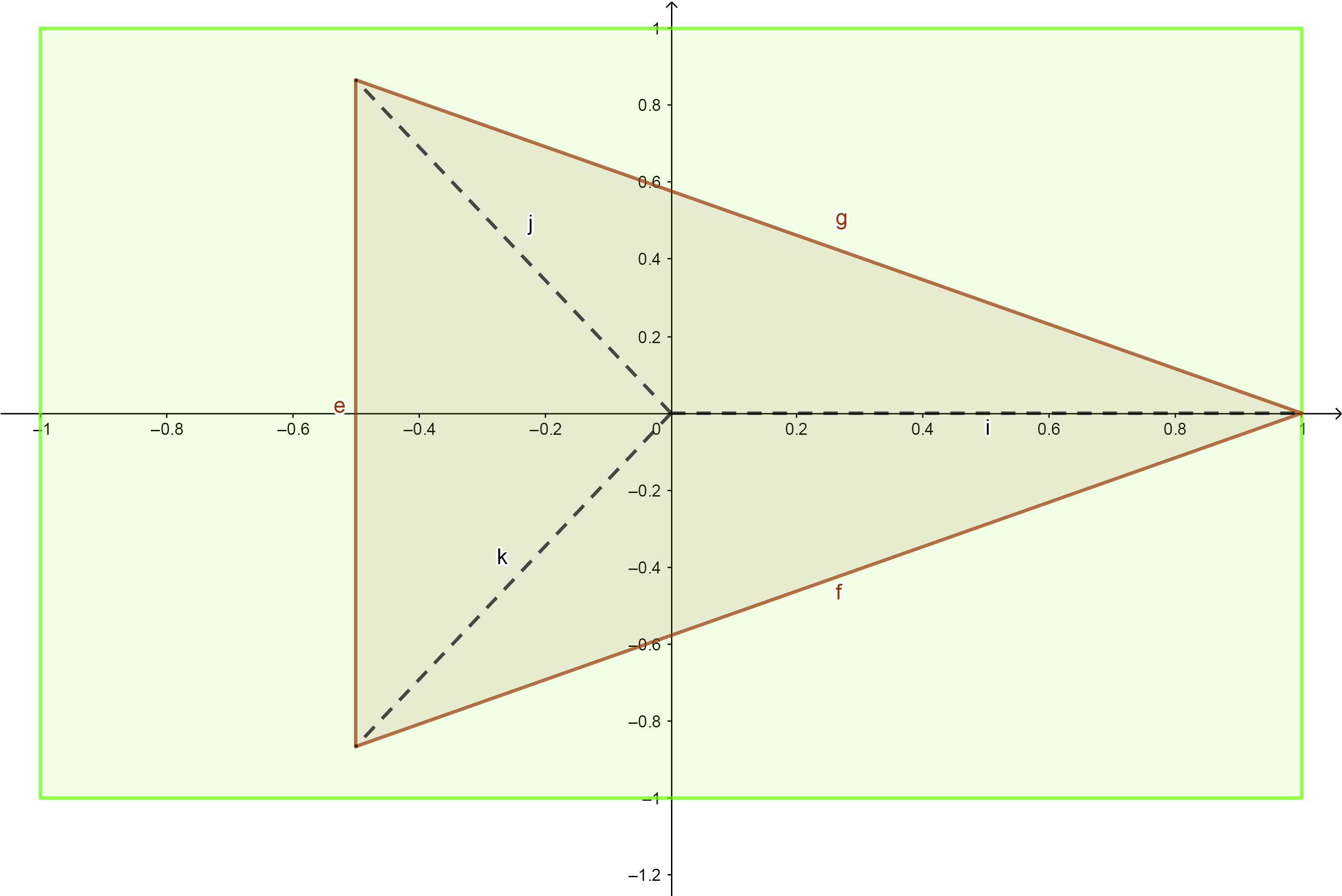
这样看起来有点不太舒服,翻转XY轴,可以得到如下效果:
float a = atan2(input.uv.x, input.uv.y) + PI;
最终的效果如下:

4、矩形
这里比较简单,添加一个Vector类型的属性接口,x、y、z、w分别代表矩形区域的四条边与UV四条边的距离。
一个片元到四条边的距离必须都满足条件,才认为在矩形内部。
//border : (left, right, bottom, top), all should be [0, 1]
float Rect(float4 border, float2 uv)
{
float v1 = step(border.x, uv.x);
float v2 = step(border.y, 1 - uv.x);
float v3 = step(border.z, uv.y);
float v4 = step(border.w, 1 - uv.y);
return v1 * v2 * v3 * v4;
}
5、直线
一般直线的方程是
y
=
k
x
+
b
y = kx + b
y=kx+b,根据给定的两点
(
x
1
,
y
1
)
(x_1,y_1)
(x1,y1)、
(
x
2
,
y
2
)
(x_2,y_2)
(x2,y2),可以分别求出
k
k
k、
b
b
b:
{
k
=
(
y
2
−
y
1
)
/
(
x
2
−
x
1
)
b
=
y
1
−
k
∗
x
1
\begin{cases} k = (y_2 - y_1)/(x_2 - x_1) \\ b = y_1 - k * x_1 \\ \end{cases}
{k=(y2−y1)/(x2−x1)b=y1−k∗x1
下一步,就是求平面任意一点到直线的垂直距离。如下图:

直线与X轴正方形的夹角为 β \beta β,根据相似三角形法则,可以求得: c o s ( β ) = 1 / k 2 + 1 cos(\beta) = 1/\sqrt{k^2+1} cos(β)=1/k2+1。
同样,根据等角原理, γ = β \gamma = \beta γ=β,所以 c o s ( γ ) = c o s ( β ) cos(\gamma) = cos(\beta) cos(γ)=cos(β)。
而任意一点距离直线的距离为 i i i,距离直线的垂直距离为 g g g,所以可以求得 i = g ∗ c o s ( γ ) i = g * cos(\gamma) i=g∗cos(γ)。
最后,根据上面求出的距离 i i i与配置的直线的宽度比较,可以判断一个点是否在直线上。
float k = (point1.y - point2.y) / (point1.x - point2.x);
float b = point1.y - k * point1.x;
float d = abs(k * uv.x - uv.y + b) / sqrt(k * k + 1);
float t = smoothstep(width/2.0, width/2.0 + aa, d);

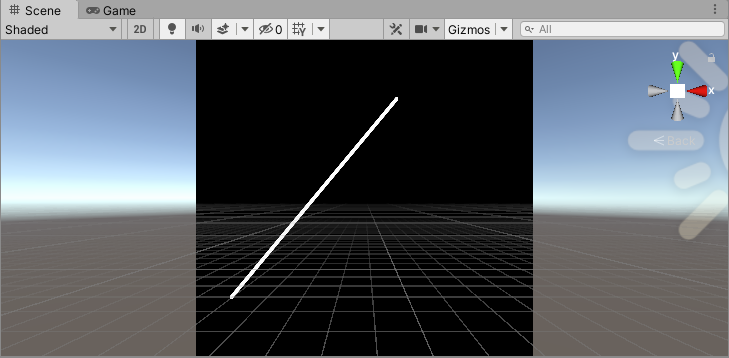
6、线段
与上面画直线的原理相同,只是需要根据给定的两点的坐标,把直线“截断”。
7、方程
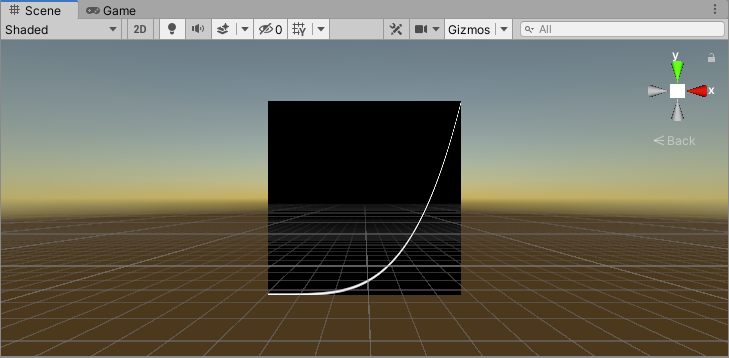
与上面画直线、线段的思路类似。不过上面是先根据两点计算出直线的方程,这里是直接给出曲线的方程。判断平面上一点是否在曲线上,这里只是简单比较垂直方向的距离,所以曲线的粗细不一致。
float Equation(float2 uv, float kx)
{
return smoothstep(kx - 0.01, kx, uv.y) - smoothstep(kx, kx + 0.01, uv.y);
}
8、点
给定一个坐标点和尺寸,判断平面上任意一点是否在区域内。思路是分别判断x、y到坐标点的距离是否都在范围内,只有都在范围内,才认为点在区域内。
float Point(float2 position, float size, float2 uv)
{
float2 v = 1 - step(size / 2.0, abs(uv - position.xy));
return v.x * v.y;
}

9、同心圆
这里先介绍一下
f
r
a
c
frac
frac函数。
f
r
a
c
frac
frac函数返回标量或每个矢量中各分量的小数部分。观察下图可以发现,对于函数
f
r
a
c
(
a
x
)
frac(ax)
frac(ax),随着
a
a
a的增大,线条逐渐变密。

先求出平面上一点距离圆心的距离,然后以距离作为上面的变量 x x x,以配置的同心圆的数量作为上面的变量 a a a,当同心圆数量为10时,可以得到下面的图:
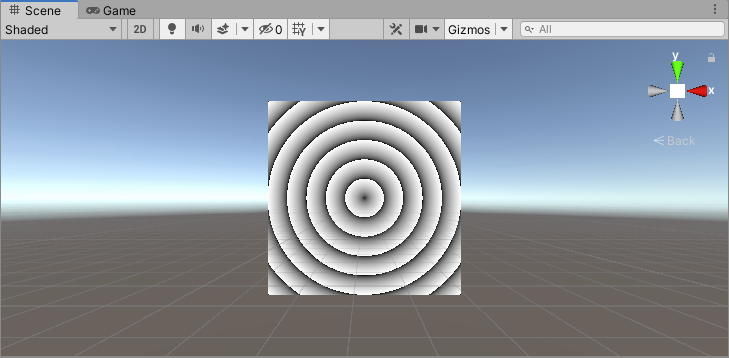
可以发现,圆环与圆环之间区域的颜色是有过度的,可以对上面的结果使用 S t e p Step Step函数截取,非黑即白。如下图:
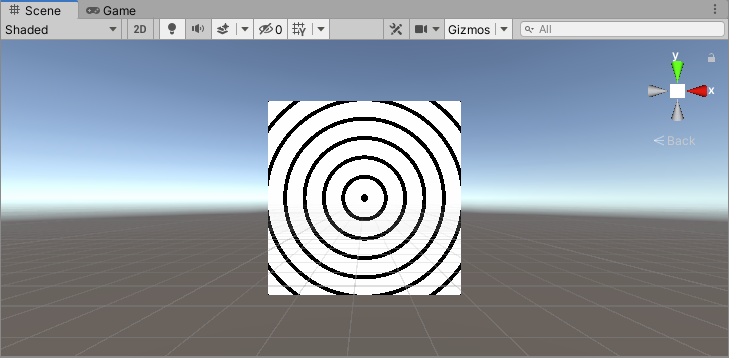
10、多个圆
同样是利用 f r a c frac frac函数。平面上点的X、Y方向的范围都是 [ 0 , 1 ] [0,1] [0,1],经过 f r a c frac frac作用后,随着圆的数量的变换如下:
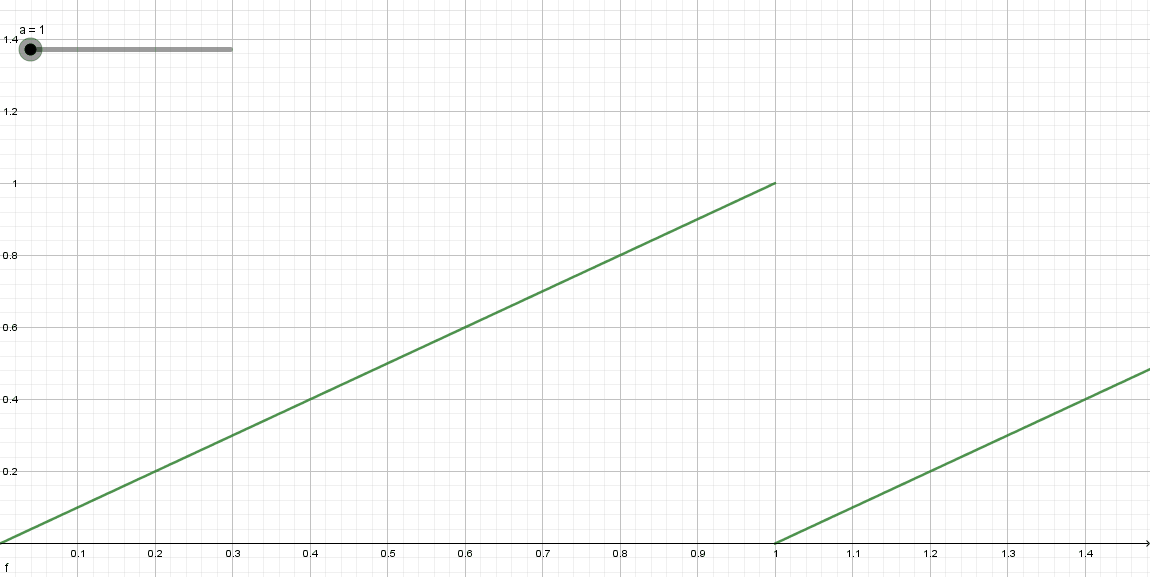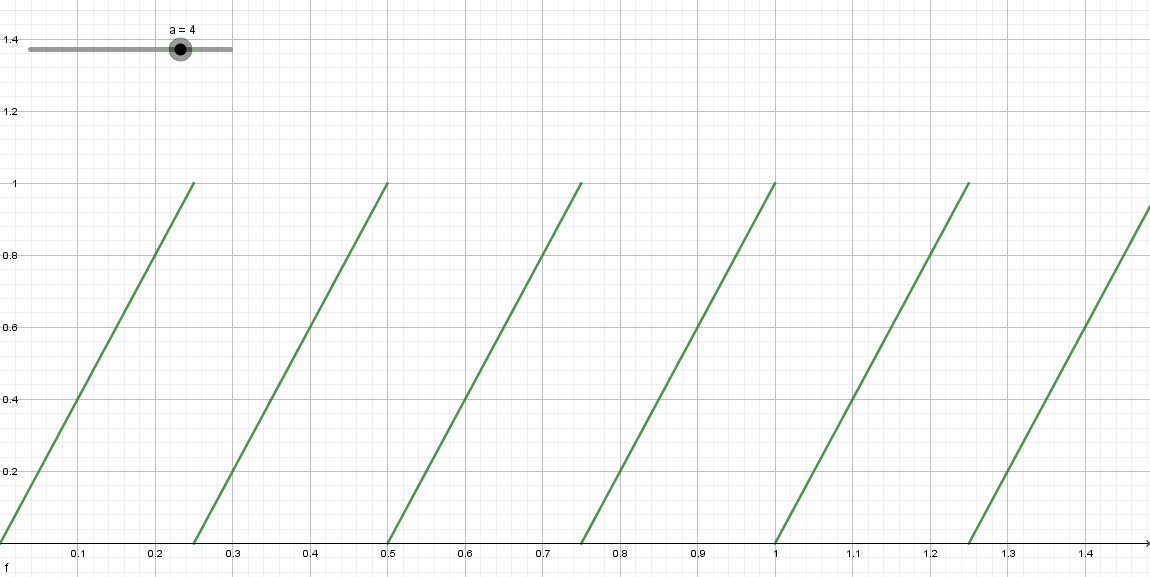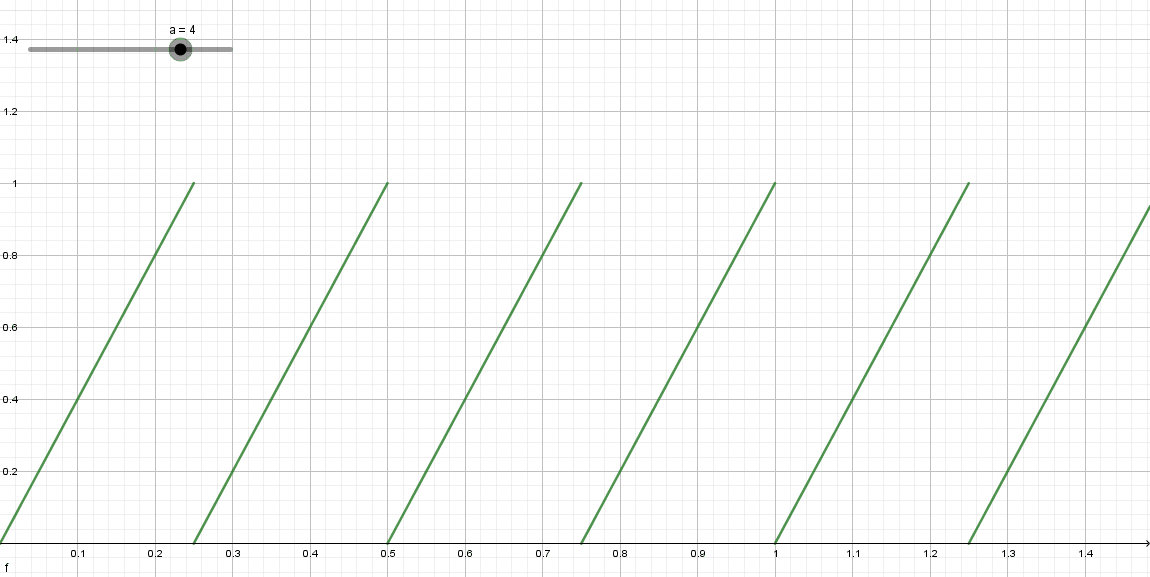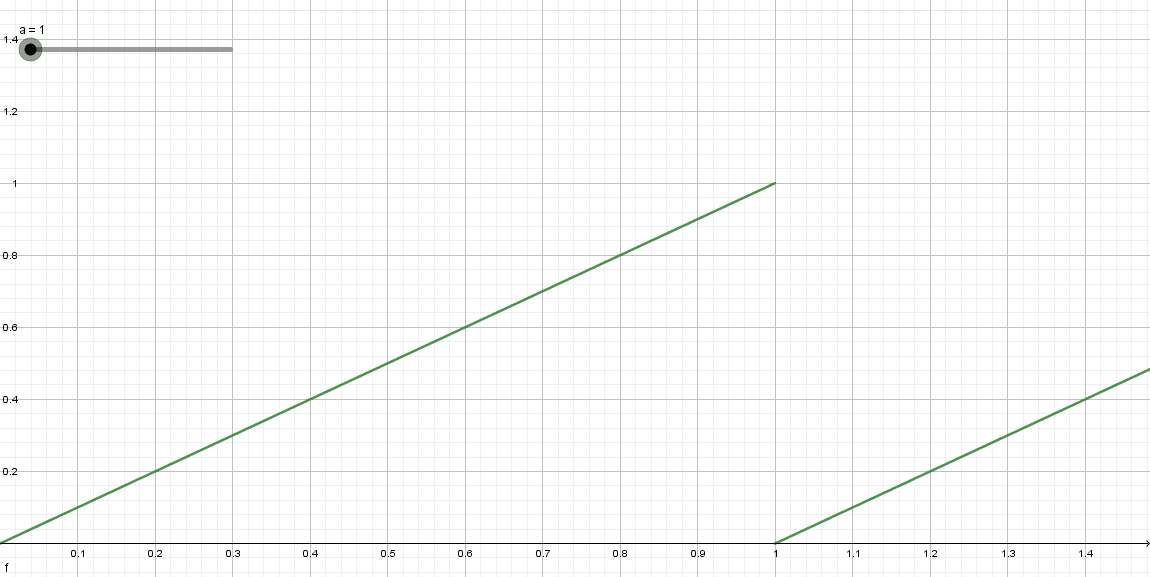
相当于对UV坐标做了 S c a l e Scale Scale变换。此时,再根据圆心和半径判断一个点是否在圆内。
float2 st = frac(input.uv * _Num);
half3 col = Circle(_Center, _Radius, st);
float Circle(float2 center, float radius, float2 uv)
{
return 1 - step(radius, distance(uv, center));
}
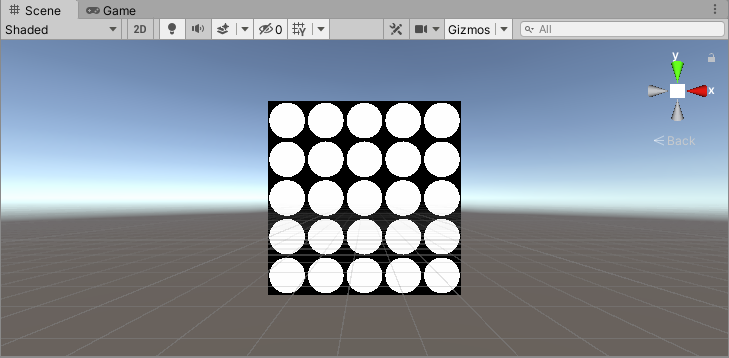
11、多个同心圆
这个比较简单,先执行上面“多个圆”的操作,再执行上面“同心圆”的操作,即可得到效果。
12、同心圆(1)
首先,在9、同心圆的基础上修改圆心为 ( 0.3 , 0.3 ) (0.3,0.3) (0.3,0.3),不进行 s t e p step step操作,可得到如下图像:
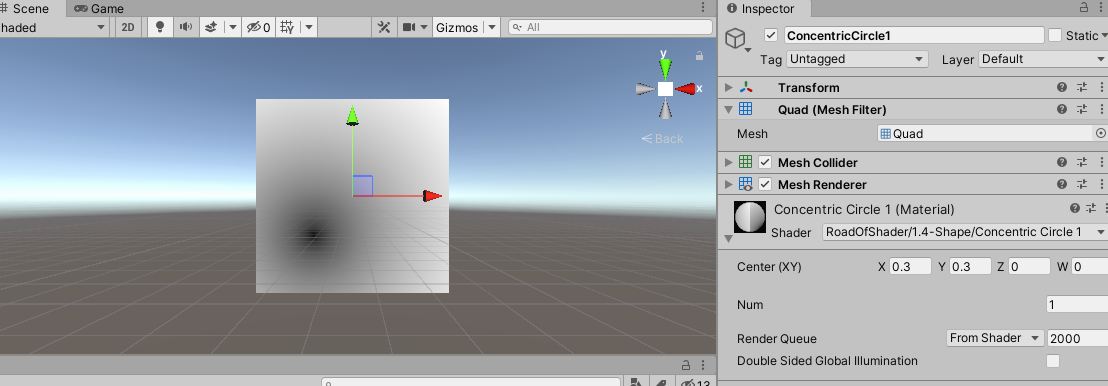
然后,将UV坐标从 [ 0 , 1 ] [0,1] [0,1]映射到 [ − 1 , − 1 ] [-1,-1] [−1,−1],即执行:
float2 st = input.uv * 2 - 1;
可以得到如下图像:
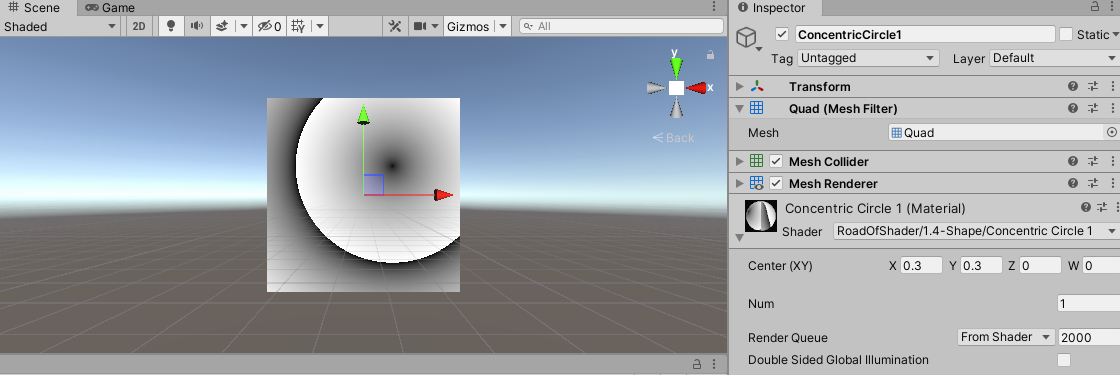
可以看到,是圆心为 ( 0.3 , 0.3 ) (0.3,0.3) (0.3,0.3)的同心圆。
下一步,对上面的UV坐标取绝对值操作。相当于第二、三、四象限的图像,都是第一象限图像的镜像。如下图:
float2 st = abs(input.uv * 2 - 1);
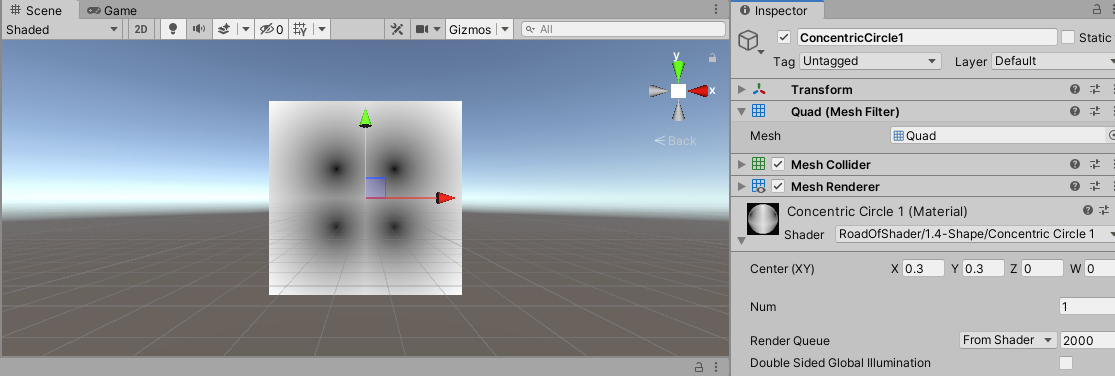
调节Num到合适的值,就可以得到如下图:
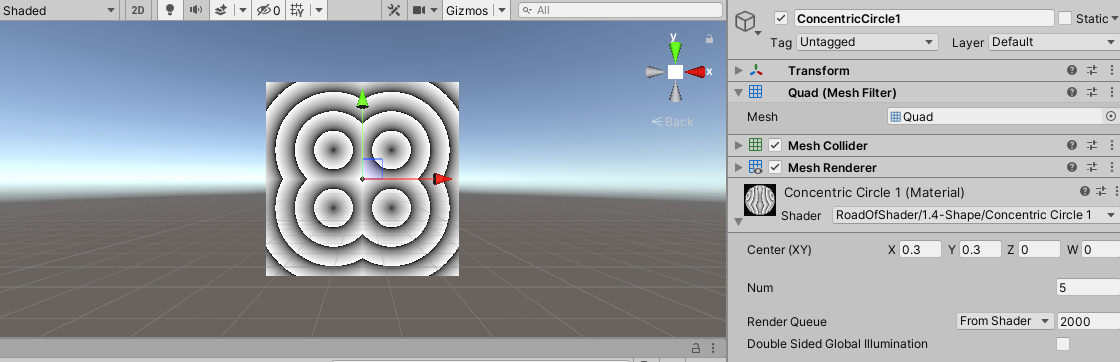
13、同心圆(2)
首先,将UV坐标从 [ 0 , 1 ] [0,1] [0,1]映射到 [ − 1 , − 1 ] [-1,-1] [−1,−1],即执行:
float2 st = input.uv * 2 - 1;
直线 m i n ( s t , 0 ) min(st, 0) min(st,0)操作,相当于把第二象限“压缩”到X轴负方向,把第四象限“压缩”到Y轴负方向,把第一象限“压缩”到原点,第三象限不变。
然后执行:
float v = distance(min(st - _Val, 0), _Center);
当 _ V a l = 0 \_Val = 0 _Val=0时,此时,对于第二象限,v只与X的值有关,表现为同一垂直方向图案相同;对于第四象限,v只与Y的值有关,表现为同一水平方向,图案相同;对于第一象限,都“压缩”到了原点,所以v值相同,表现为同一颜色;第三象限正常表现同心圆现象。如下图:
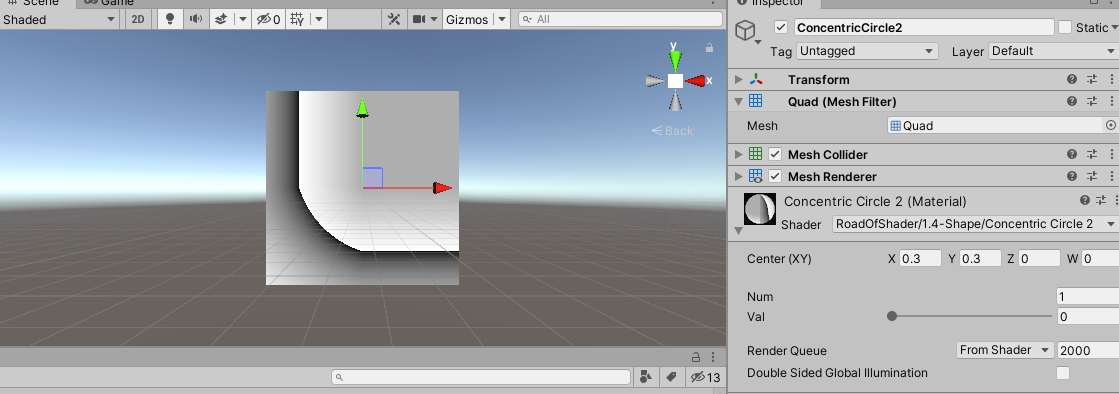
对于 _ V a l \_Val _Val的改变,相当于是平移了圆心。
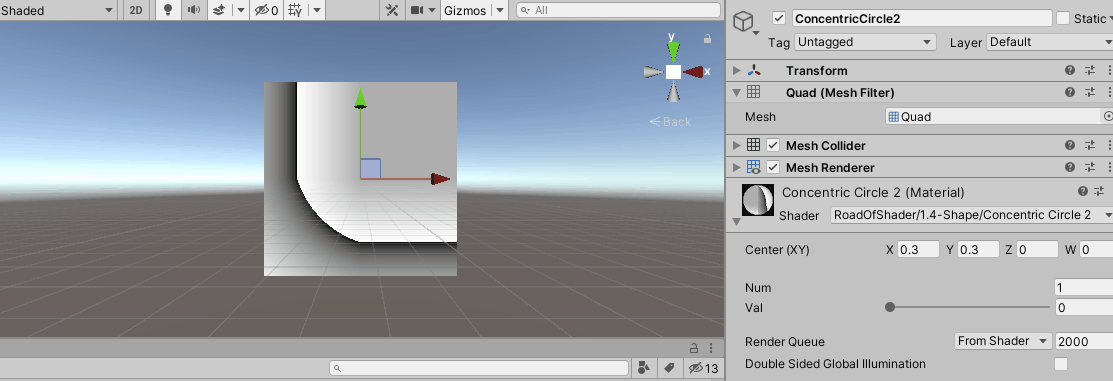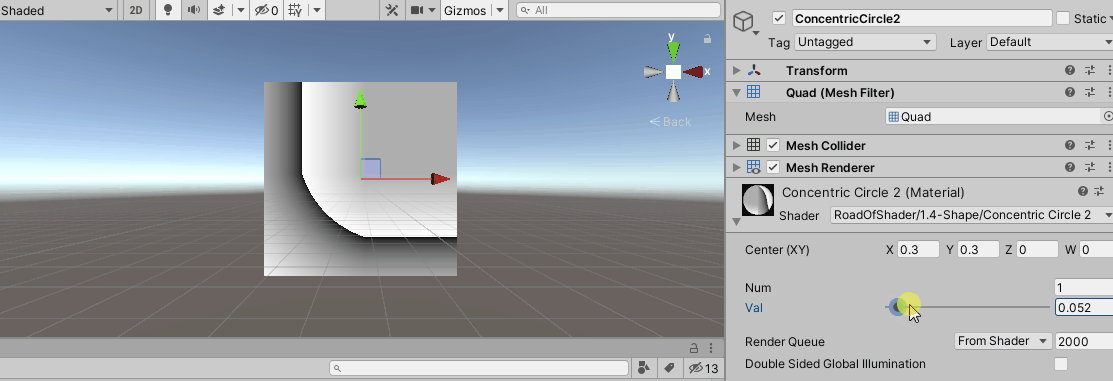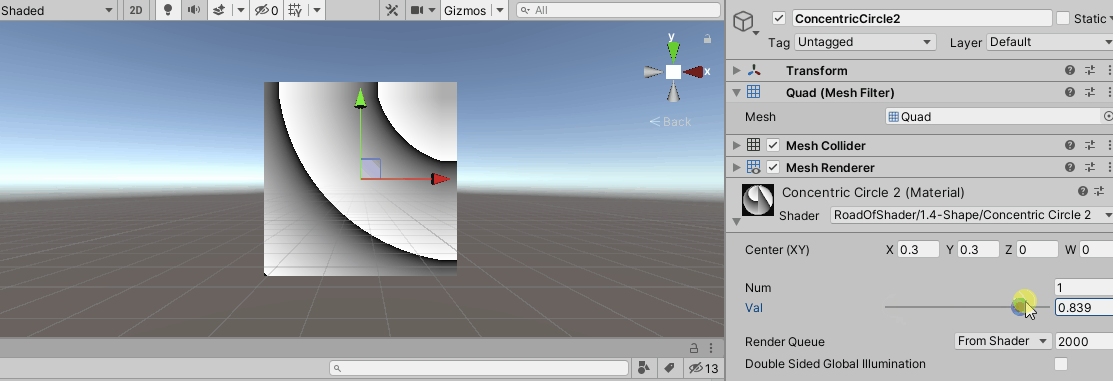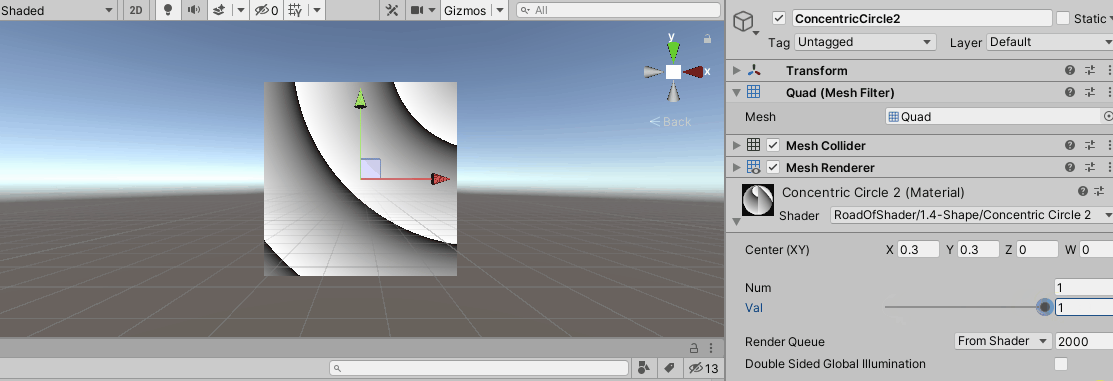
调整属性,可以得到如下图像:
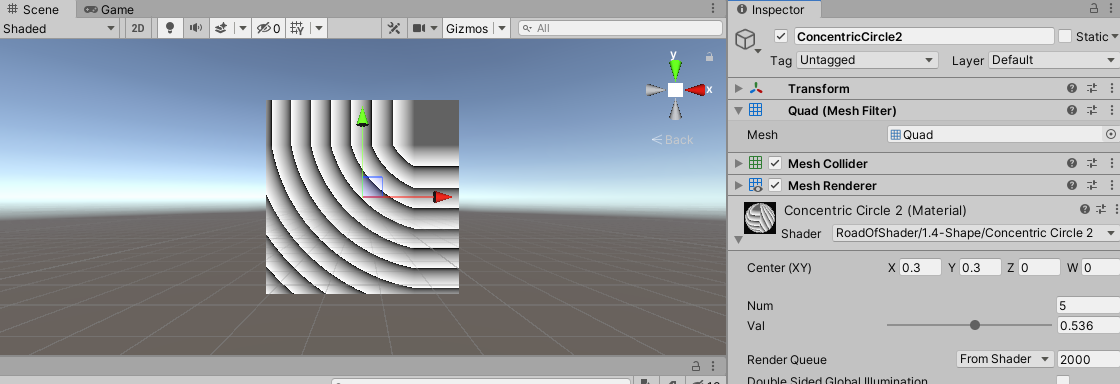
再对UV取绝对值,相当于其它三个象限的图像都是第一象限的镜像,可以得到:
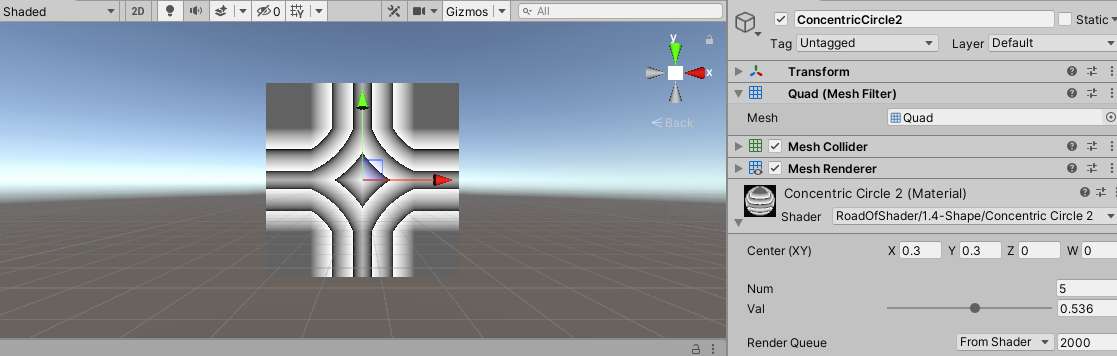
14、同心圆(3)
与上面的同心圆(2)的原理基本类似,只是上面是执行 m i n min min操作,这里是执行 m a x max max操作,其它流程都相同,这里不再赘述。
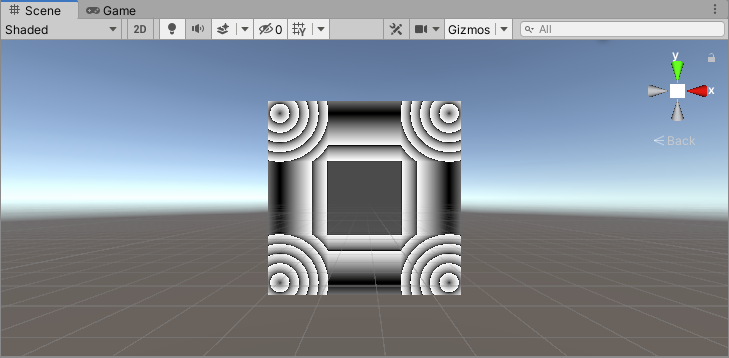
15、同心圆(4)
首先,将UV坐标从 [ 0 , 1 ] [0,1] [0,1]映射到 [ − 1 , − 1 ] [-1,-1] [−1,−1],即执行:
float2 st = input.uv * 2 - 1;
然后计算平面上每个点到圆心的距离,使用距离和一个阈值执行 s t e p step step操作,即可得到如下图像:
float v = distance(st, _Center);
half3 col = step(_Val, v);
return half4(col, 1.0);
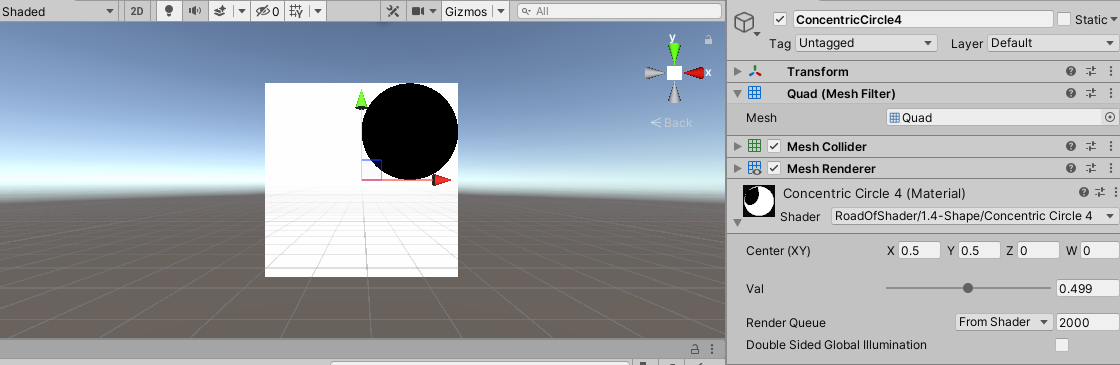
再对UV取绝对值,相当于其它三个象限的图像都是第一象限的镜像,可以得到:
float2 st = abs(input.uv * 2 - 1);
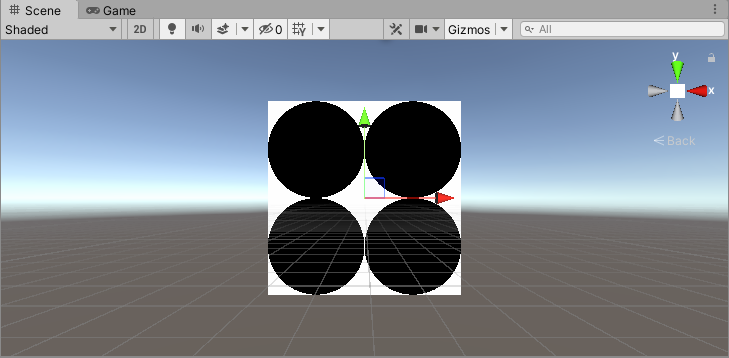
16、同心圆(5)
与上面类似,只是不是使用一个阈值判断,而是使用两个阈值确定一个范围。
float2 st = abs(input.uv * 2 - 1);
float v = distance(st, _Center);
half3 col = step(_Val, v) * step(v, _Val2);
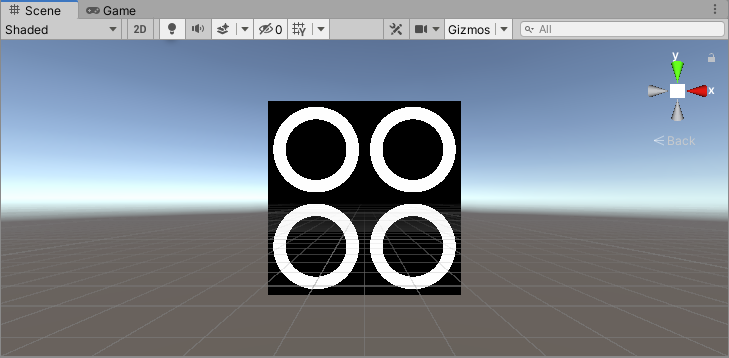
17、极坐标图案(1)
先对UV坐标进行平移,使 ( 0 , 0 ) (0,0) (0,0)在UV坐标的中心。
float2 uv = input.uv - 0.5;
然后,计算平面上每个点的极坐标的角度值。
float a = atan2(uv.y, uv.x);
对于第一、二象限,a的值域是 [ 0 , π ] [0,\pi] [0,π],第三、四象限与第二、一象限对称。这里只分析第一、二象限。
对于 [ 0 , π ] [0,\pi] [0,π]的定义域, c o s cos cos函数的图像如下图:
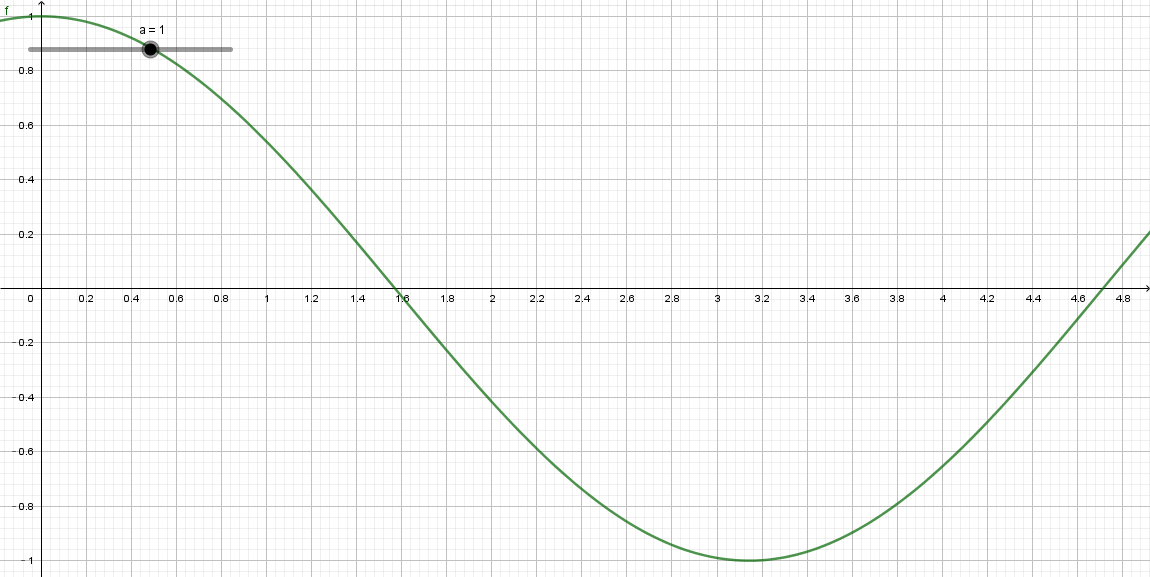
可以发现,函数在 [ 0 , π ] [0,\pi] [0,π]范围内是单调递减的。得到的图案的效果是:在第一象限颜色逐渐变暗;在第二象限,由于 c o s cos cos的值是负值,所以全部是黑色。如下图:

随着Num的变化,逐渐得到如下图案:

18、极坐标图案(2)
首先,将UV坐标的中心移动到原点。
float2 uv = input.uv - 0.5; //[-0.5, 0.5], make (0,0) in the center
然后,转化为极坐标系,画出 c o s ( θ ) cos(\theta) cos(θ)的图案,如下图:
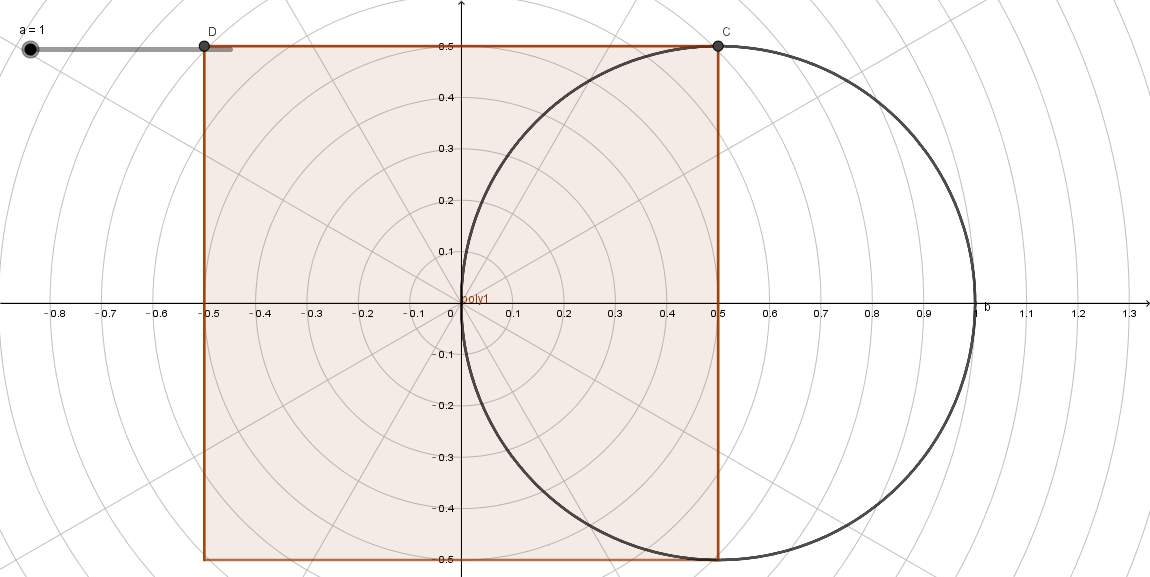
UV点坐标的长度,其实就是上述整个矩形区域,为了使矩形能完全包含圆形区域,将UV点坐标的长度扩大两倍。
float r = length(uv) * 2.0;

将UV点长度与极轴的距离做对比,可以发现,在圆形区域内,UV点长度小于极轴的距离,反映在图像上,如下所示:
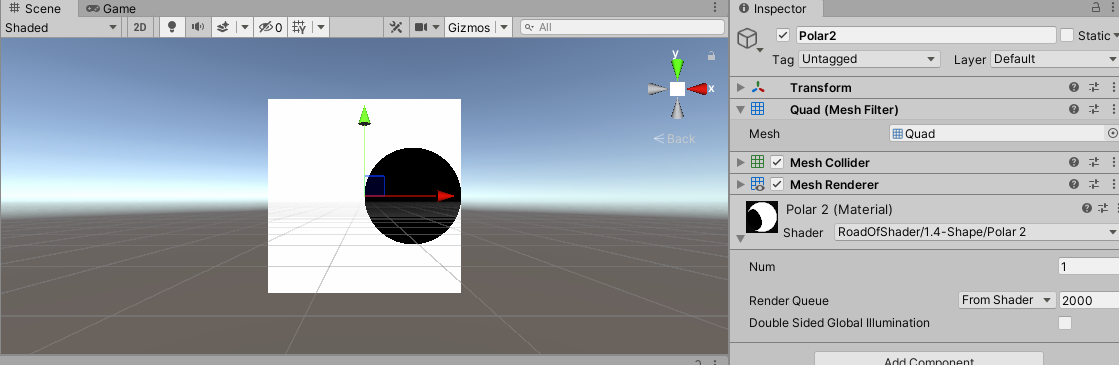
当 N u m = 2 Num = 2 Num=2时,在坐标系中的关系如下图:
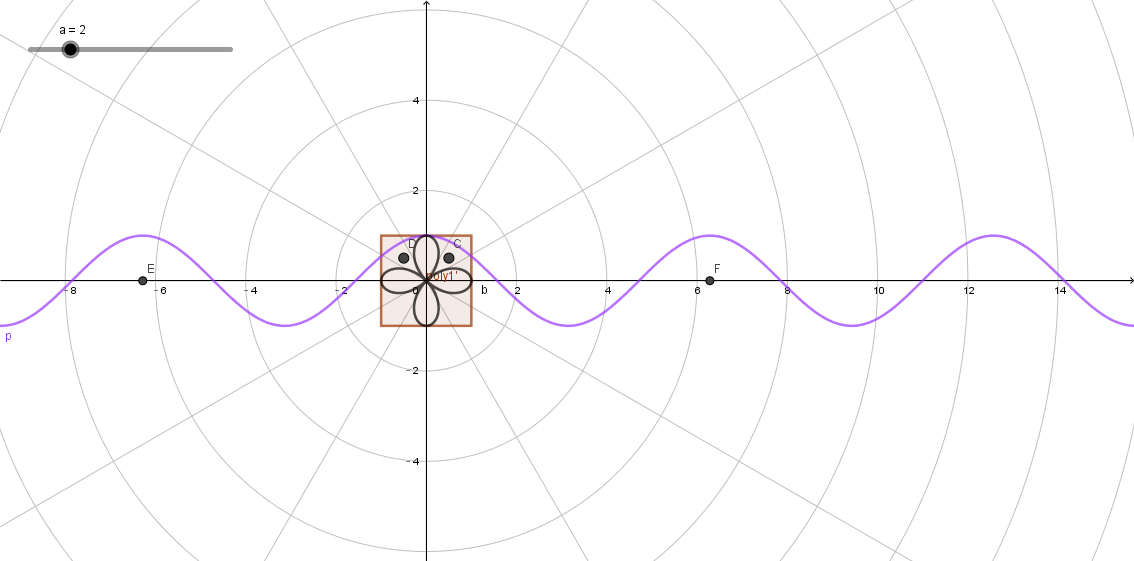
此时,余弦曲线的定义域是 [ − 2 π , 2 π ] [-2\pi,2\pi] [−2π,2π],对于X正方形 [ 0 , 2 π ] [0,2\pi] [0,2π]范围,有两个大于0的“凸起”,在此范围内,极轴的距离大于UV点的长度;而对于其他小于0的范围,极轴的距离为负值,而UV点的长度始终为正值,所以极轴的距离肯定小于UV点的长度。对于 [ − 2 π , 0 ] [-2\pi,0] [−2π,0]范围,与上面对称,不再赘述。
此时的图案如下图,与上面的分析吻合。
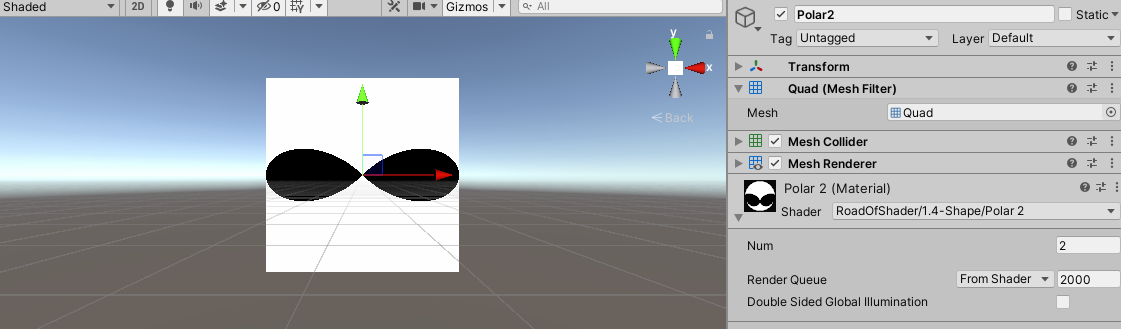
通过调节 N u m Num Num的值,最终可以得到如下的图案,相关的分析与上面相同。
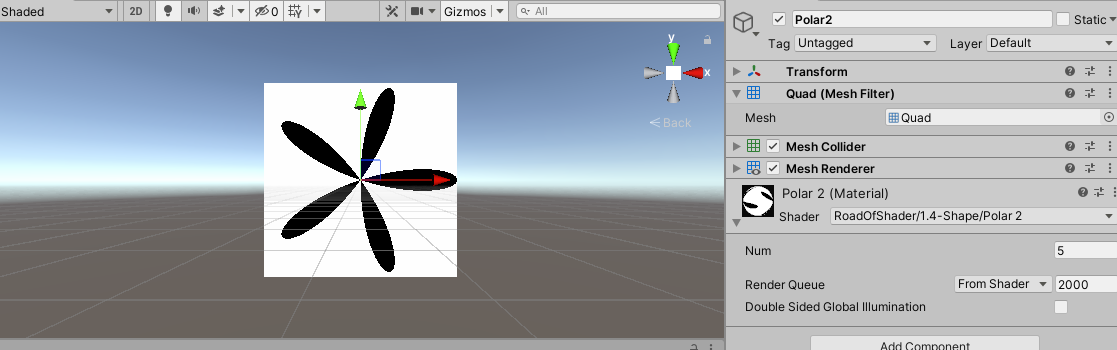
19、极坐标图案(3)
可以看到,上面得到的极坐标图案(2)边缘处非常锐利。这里将对其进行改善,柔化边缘。使用的方法,主要是使用smoothstep函数替代step函数,然后再添加了一个柔和**_Smooth**属性,其它都基本相同。
half3 col = smoothstep(f, f + _Smooth, r);
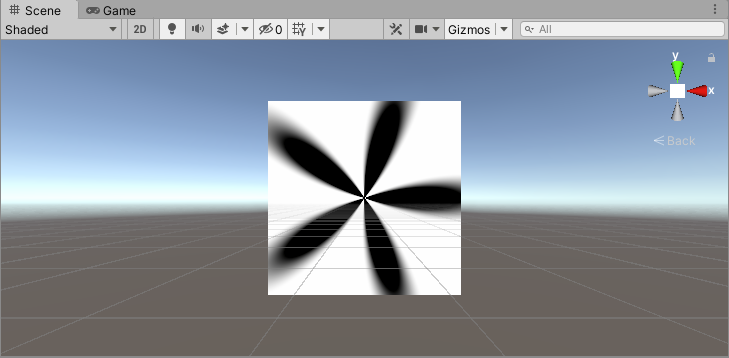
20、极坐标图案(4)
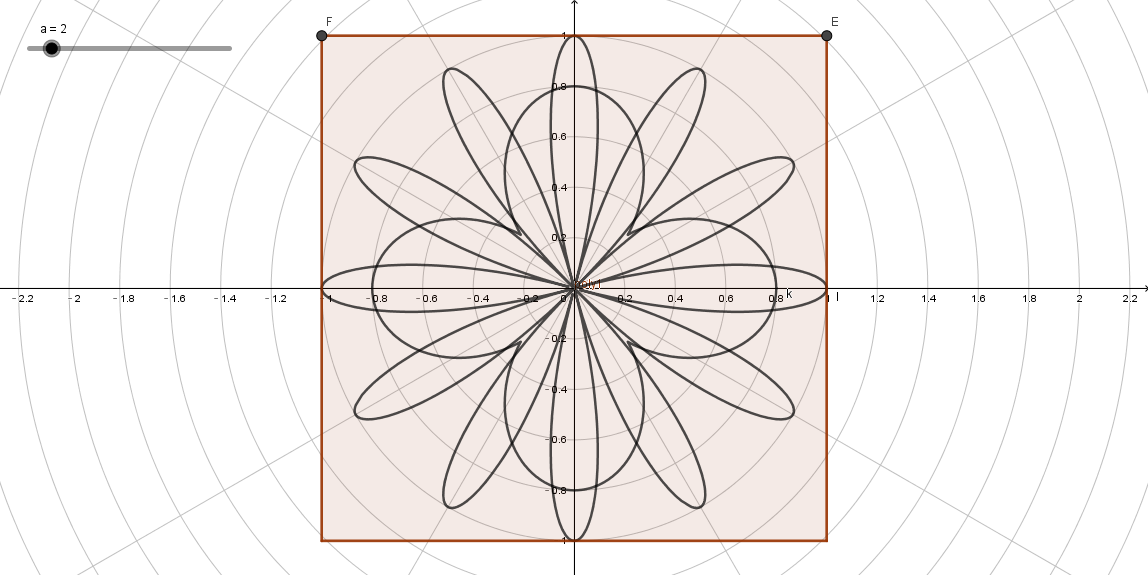
这里,也是在**极坐标图案(2)**的基础上改的,主要的区别是极坐标曲线不同。
float f = abs(cos(a)) * 0.5 + 0.3;
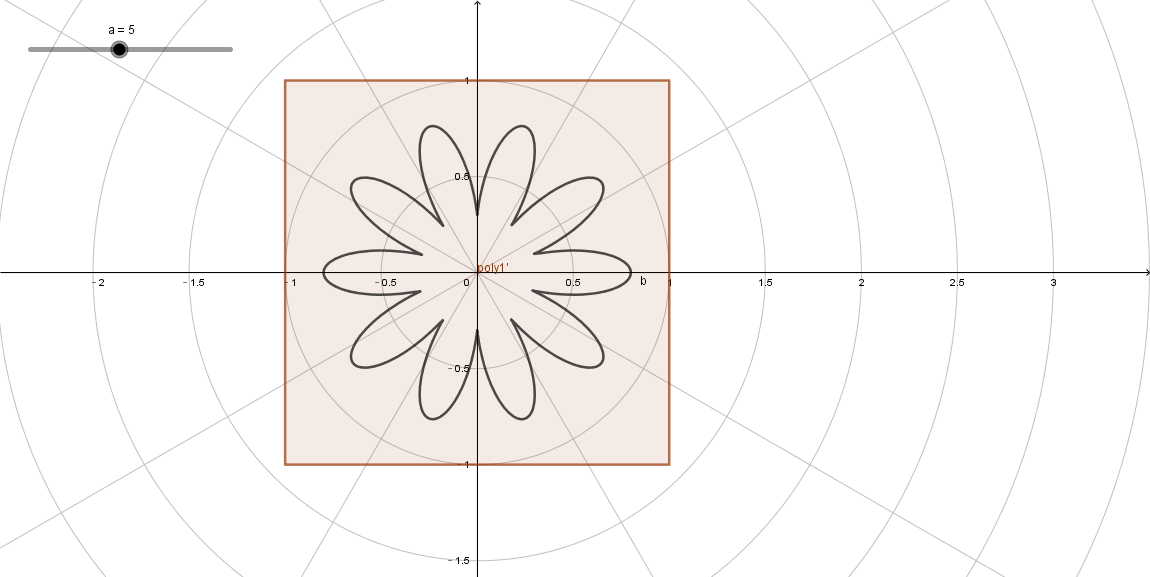
21、 极坐标图案(5)
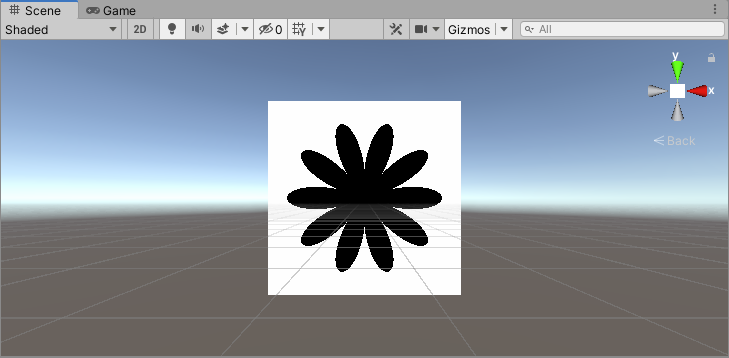
这里,也是在**极坐标图案(2)**的基础上改的,主要的区别是极坐标曲线不同。
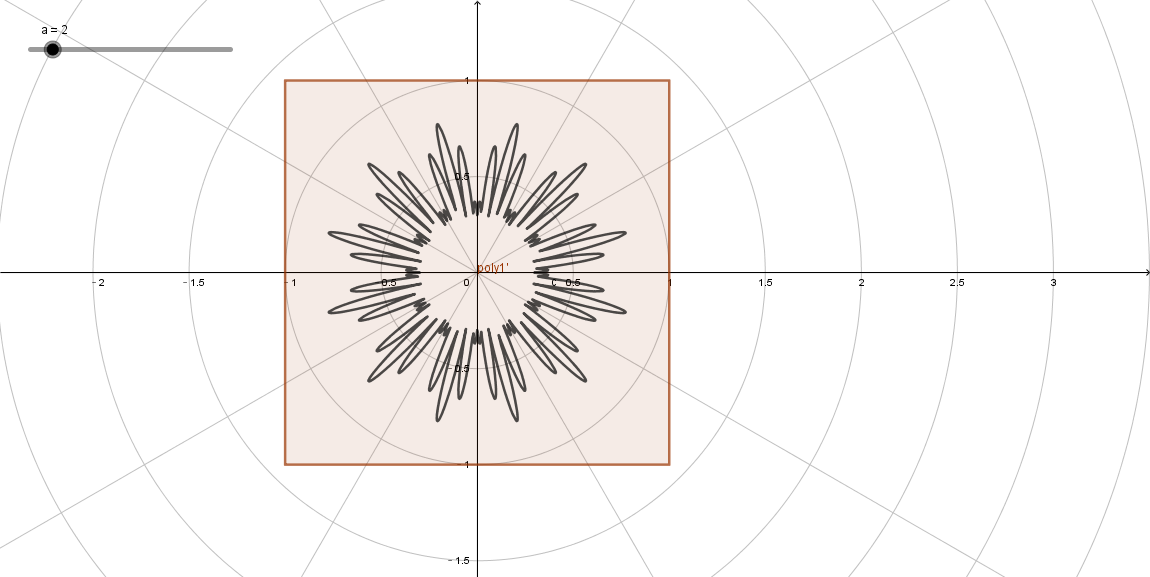
float f = abs(cos(a * 12) * sin(a * 3)) * 0.5 + 0.3;
22、极坐标图案(6)
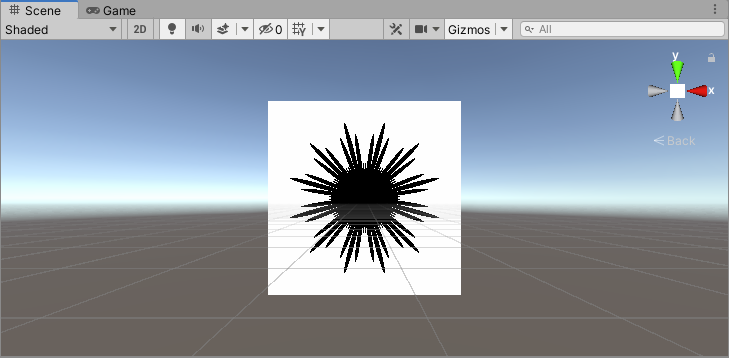
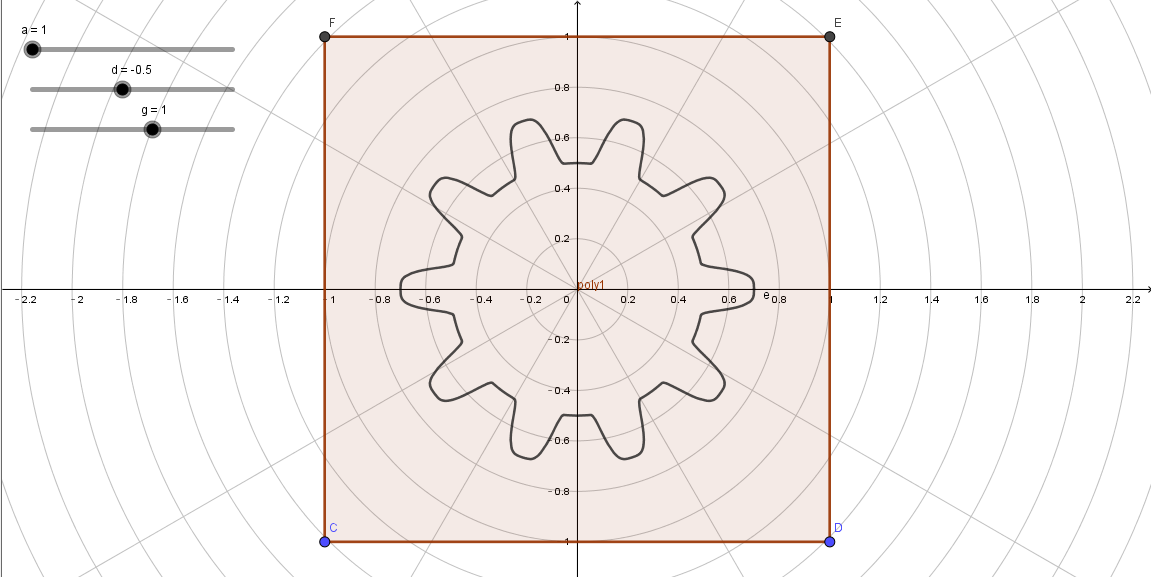
这里,也是在**极坐标图案(2)**的基础上改的,主要的区别是极坐标曲线不同。
float f = smoothstep(-0.5, 1.0, cos(a * 10)) * 0.2 + 0.5;
23、极坐标图案(7)
这里,也是在**极坐标图案(2)**的基础上改的,但相比较上面几个,这个更复杂了,牵涉到了图像的并集、补集等。
首先,定义了两个极坐标曲线:
float f = abs(cos(a)) * 0.5 + 0.3;
float f2 = abs(cos(a * 3));
然后,下面的代码的意思是,子集f在集合r中的补集:
1 - step(f, r)
而下面代码的意思是,两个补集的并集,即r中不属于f或f2的区域:
half3 col = (1 - step(f, r)) + (1 - step(f2, r));
下面的代码,得出的是r中属于f或f2的区域:
col = 1 - col;
最终,可以得到如下图案:
24、并集
这里比较简单,上面介绍了1、圆形和4、矩形,这里是为了得到二者的并集。
return Rect(_Border, input.uv) + Circle(_CircleCenter.xy, _CircleRadius, input.uv);
25、差集
与上面类似,不过这里不是求并集,而是求差集,即属于矩形,但不属于圆形的区域。
return Rect(_Border, input.uv) - Circle(_CircleCenter.xy, _CircleRadius, input.uv);
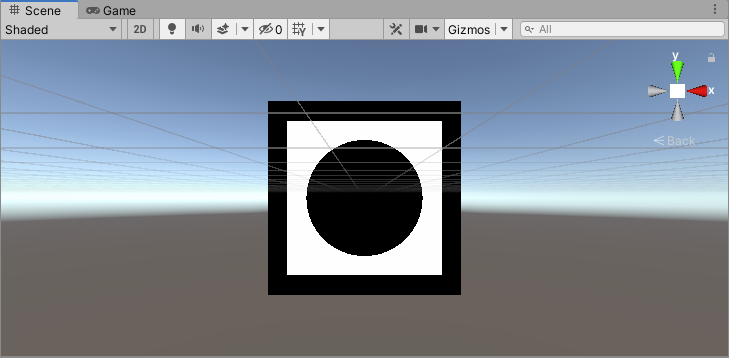
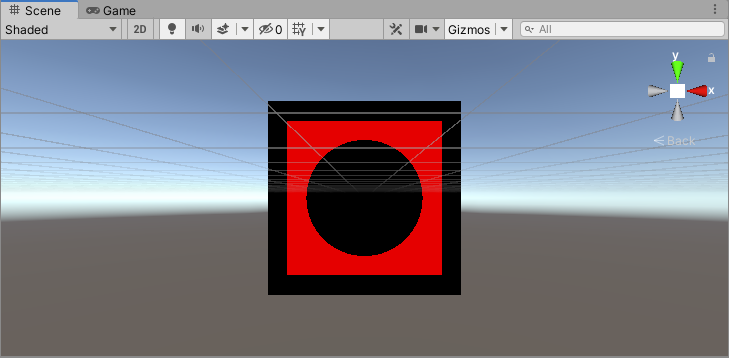
26、带颜色的差集
在上面差集的基础之上,添加一些颜色。
float v = Rect(_Border, input.uv) - Circle(_CircleCenter.xy, _CircleRadius, input.uv);
return v * _Color;
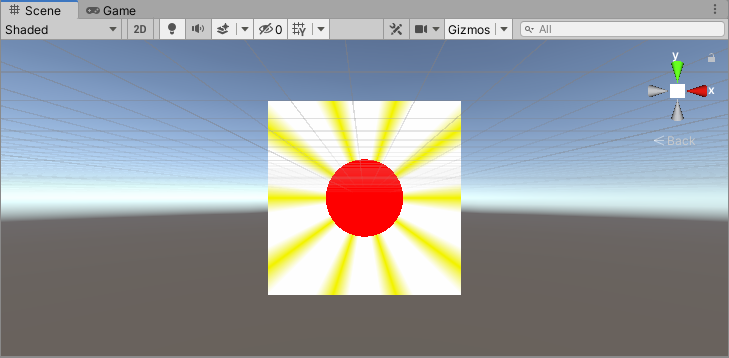
27、日出
这里,在1、圆形和**17、极坐标图案(1)**的基础上改进。
首先,得出极坐标图案和圆形区域:
float f = cos(a);
float cir = Circle(float2(0.5, 0.5), 0.2, input.uv);
给圆形区域赋予红色:
half3 circleCol = cir * half3(1,0,0);
对于非圆形区域,对不属于f的区域赋予白色,对属于f的区域赋予颜色half3(0.9,0.9,0):
half3 lineCol = (1 - cir) * ((1 - f) + f * half3(0.9,0.9,0));
最后,把圆形区域的颜色和线的颜色相加,即可得到最终效果:
half3 col = circleCol + lineCol;
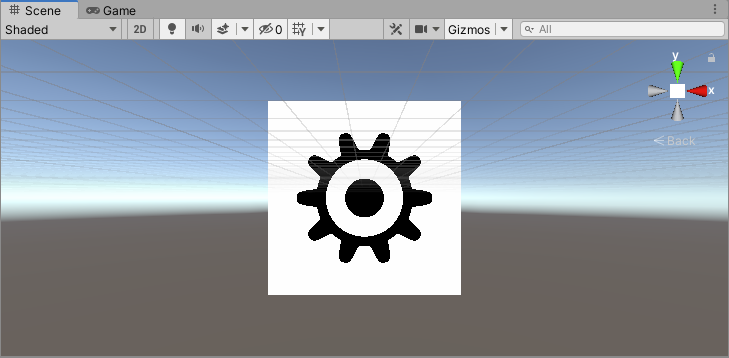
28、齿轮
这里,在1、圆形和**22、极坐标图案(6)**的基础上改进。
首先,得出三个图形区域:
float v1 = smoothstep(-0.5, 1.0, cos(a * 10)) * 0.2 + 0.5;
float v2 = Circle(float2(0.5,0.5), 0.2, input.uv);
float v3 = 1 - Circle(float2(0.5,0.5), 0.1, input.uv);
然后,先求v1与矩形区域的交集,再求v2和v3之间的交集,最后,求出两个交集之间的并集:
half3 col = step(v1, r) + v2 * v3;
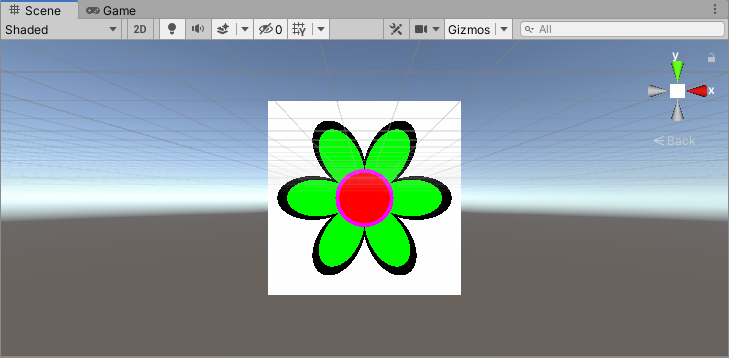
29、花朵
这里,在1、圆形和**22、极坐标图案(4)**的基础上改进。
首先,得出三个图像区域:
float f = abs(cos(a)) * 0.5 + 0.3;
float cir = Circle(float2(0.5, 0.5), 0.15, input.uv);
float cir2 = Circle(float2(0.5, 0.5), 0.13, input.uv);
然后,给“花瓣”着色。1 - cir保证花瓣的函数在大圆之外执行,step(f, r) * step(r, f + 0.1)描边,(1 - step(f, r)) * fixed3(1, 0, 1)花瓣着色。1减去上面的结果,相当于简单的颜色相减。
half3 col1 = (1 - cir) * (1 - (step(f, r) * step(r, f + 0.1) + (1 - step(f, r)) * half3(1, 0, 1)));
接着,得出中间圆形区域的颜色。先计算cir2之外,属于cir的区域的颜色;再计算cir2区域的颜色。
half3 col2 = (1 - cir2) * cir * half3(1, 0, 1) + cir2 * half3(1, 0, 0);
最后,得出最终的颜色。
half3 col = col1 + col2;
参考
- [1] 动态几何画板Geogebra教学应用
- [2] 《Unity Shader入门精要》
- [3] atan2
- [4] Shader实验室:frac函数






















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








