经典文献阅读之--GRIL‑Calib(无目标IMU‑LiDAR外在校准方法)

写在前面

**摘要：**随着IMU‑LiDAR融合系统重要性的增加，无目标IMU‑LiDAR外在校准方法越来越受到关注。现有的校准方法需要在所有轴上完全运动的情况下推导校准参数。当IMU和LiDAR安装在地面机器人上且其运动仅限于平面运动时，现有的校准方法可能会表现出性能下降，为了解决这个问题，我们提出GRIL‑Calib：一种新颖的无目标地面机器人IMU‑LiDAR校准方法。我们提出的方法利用地面信息来补偿不受限制的全运动的缺乏。**首先，我们提出使用地平面残差来提高校准精度的激光雷达里程计（LO）。其次，我们提出了地平面运动（GPM）约束并将其纳入校准优化中，从而能够确定完整的6‑DoF外在参数，包括理论上不可观测的方向。最后，与基线方法不同，我们没有将校准看作连续的两次优化，而是看作单个优化（SO）问题，同时求解所有校准参数并提高准确性。**我们通过将GRIL‑Calib应用到三个公共现实数据集，并将其性能与现有最先进方法在准确性和鲁棒性方面的性能进行比较来验证GRIL‑Calib。

代码可在https://github.com/Taeyoung96/GRIL获取。

创新点导读：

本文基于FAST-LIO和LI-Init的IESKF算法改进了两点：

（1）地面约束引入到雷达里程计BA优化降低z轴漂移；

（2）地面约束引入到外参标定BA优化提升平面运动的可观测性。

​ 第一点地面约束提升里程计精度是典型做法，主要介绍下第二点地面约束提升外参估计精度。现有无目标约束算法通过运动约束建立激光雷达运动和IMU运动（轨迹/速度加速度等）之间的约束方程进行优化求解，要求六自由度运动，但是小车只有平面运动三自由度运动（水平两维度平移和一个航向角旋转），为了弥补缺失的三自由度（垂直方向平移、横滚和倾斜角旋转），引入地面约束，具体如下图所示。

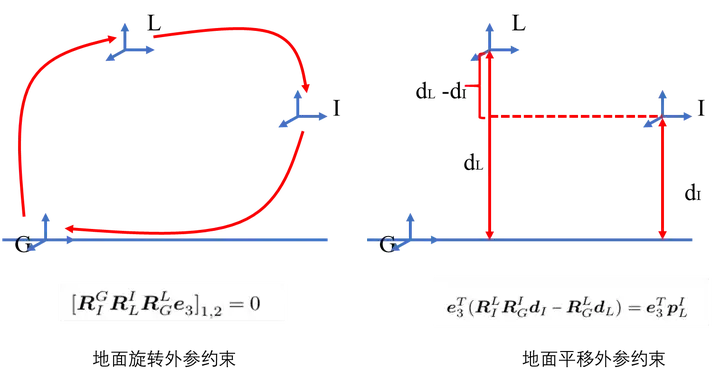
（1）引入重力方向向量，弥补横滚和倾斜角自由度缺失，具体表现为通过IMU相对于地平面的姿态和雷达相对于地面姿态构建外参旋转约束方程；

（2）引入重力方向的垂直测距值，弥补垂直方向平移，具体表现为引入L相对于G的高度dL和IMU相对与地面的高度计算垂直方向dI的平移约束方程。$dL$可以通过地面检测计算得到，$dI$手动测量（会引入误差，但IMU到地面距离实在是算不出来…）

一、简介

​ LiDAR比其他传感器获取更准确的3D信息，广泛适用于各种机器人应用，例如自我运动估计[1]、定位[2]和地图[3]系统。然而，激光雷达的缺点是当其应用于快速运动时，容易出现运动失真。最近，为了克服这个缺点，LiDAR已与IMU（惯性测量单元）[4]、[5]、[6]结合使用。IMU可以高频测量加速度和角速度，可有效补偿LiDAR的运动失真。精确的外参标定是IMU‑LiDAR融合系统的基本要求。外在标定是指在IMU和LiDAR之间建立空间变换的过程，从而将两个传感器的测量结果统一到一个坐标系[7]。

​ **针对IMU和LiDAR之间的外参标定进行了大量的研究，可分为两个方向：基于目标的方法和无目标的方法。**基于目标的方法使用已知的预定义对象（例如圆柱体[8]）来估计IMU和LiDAR之间的空间变换。基于目标的方法相对准确，但缺点是需要预先确定目标。另一方面，无目标方法不使用任何预定义的物体进行校准，由于易于使用和可重复性而受到广泛关注。相反，无目标方法需要两个传感器的综合激励运动来激活所有自由度(DoF)。对于具有集成IMU和LiDAR传感器的手持设备来说，实现这种运动非常简单，因为它们可以轻松执行全方位的运动。然而，对于地面机器人来说是一个重大挑战，因为它们的运动仅限于平面运动。

​ 此外，从理论角度来看，缺乏全运动会使Fisher信息矩阵（FIM）的秩小于其维数，而退化或秩不足的FIM将导致估计的校准参数具有较高的不确定性或不成为独特的。为了解决这个问题，一些论文进行了可观测性分析[9]、[10]、[11]，但该分析仅识别不可观测的方向，并没有直接估计外参参数。

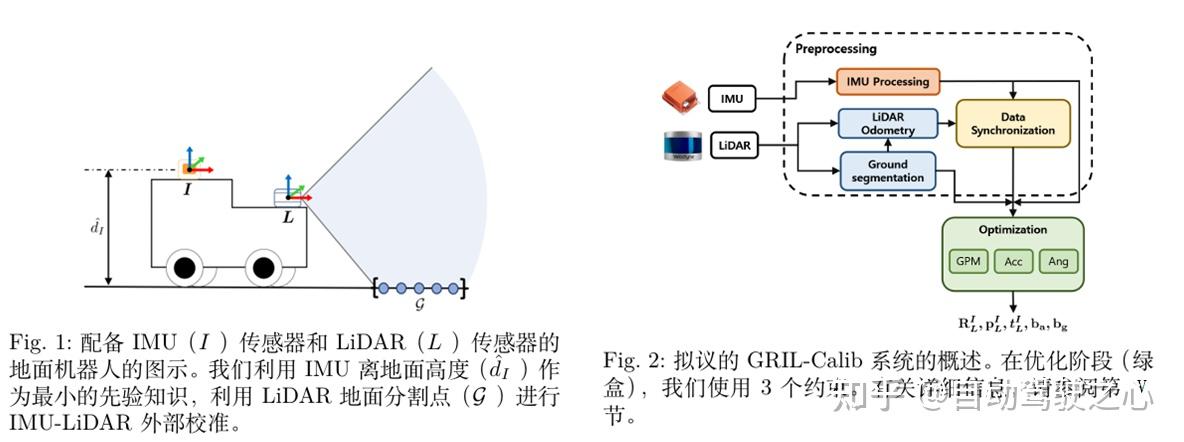
在本文中，我们提出了GRIL‑Calib：新型无目标地面机器人IMU‑LiDAR外在标定方法。为了解决上述退化问题，我们利用地平面运动（GPM）约束。GPM提供有关机器人运动的几何信息，即使某些外部参数不可观测，也允许完整的6‑DoF外部参数。地面机器人IMU和LiDAR之间的外在标定问题如图1所示。LiDAR里程计（LO）[12]或视觉惯性里程计（VIO）[13]也提出了与地面相关的类似约束。然而，我们提出了一个地平面运动（GPM)约束，专门针对IMU和LiDAR的外部标定。有关机器人运动的几何信息，即使某些外部参数不可观测，也允许完整的6‑DoF外部参数。

​ 提出了一种新颖的地面机器人IMU‑LiDAR融合系统的外在标定方法，因此不需要满足完全激励运动。

​ （１)为了提高标定性能，我们提出了一种利用地平面观测的新型激光雷达里程计（LO）。地平面残差被合并到迭代误差状态卡尔曼滤波器(IESKF)中，以减少绕z轴的漂移。

​ （２）提出了地平面运动（GPM）约束，并将该约束应用于标定的非线性优化。GPM使我们能够解决包括不可观测方向在内的参数，并提高标定精度。

​ （３）在标定的非线性优化中，我们将平移和旋转参数的标定同时制定为单一优化（SO）问题求解参数。然而，基线方法单独且顺序地标定两个参数，从而降低了标定精度。

​ （４）在M2DGR[14]、Hilti[15]和S3E[16]数据集上验证了GRIL‑Calib，与最先进的无目标方法相比，它取得了优异的结果。

​ 本文的其余部分组织如下：第二部分对最新IMU‑LiDAR标定方法进行了全面回顾。在第三节中，我们介绍了GRIL‑Calib的系统概述，并在第四节和第五节中详细描述了每个关键部分。第六节描述了在各种真实数据集上进行的实验以及结果分析。最后，第七节提供结论并讨论未来的工作。

二、相关工作

在早期的IMU-LiDAR标定研究中，需要使用任意目标进行标定[8]，[17]。然而，基于目标的方法并不实用，因此最近更多地研究了无需目标的标定方法。Subodh等人[18]提出了一种基于扩展卡尔曼滤波器（EKF）的基于运动的标定方法。此外，Lv等人[19]利用基于B样条的连续时间轨迹形式进行了研究。此外，OA-LICalib [11]扩展了他们以前的工作[19]，提出了两个观测性感知模块，旨在解决退化情况。不幸的是，所提出的观测性感知模块仅设计用于拒绝不必要的运动。FAST-LIO2 [4]是一种基于迭代误差状态卡尔曼滤波器（IESKF）的准确的LiDAR-惯性测距（LIO）算法，其中包括外部标定参数。由于强非线性，LIO系统的性能高度依赖于准确的初始状态。为了获得准确的初始状态估计，Zhu等人[20]提出了一种基于优化的算法，该算法对齐角速度和加速度。现有方法[18]，[11]，[20]需要传感器的所有轴线上的足够运动才能获得准确的结果。当应用于可以自由在各个方向移动的手持设备时，这些方法是实用的。然而，当应用于地面机器人时，现有方法会遇到挑战，因为运动仅限于平面运动。相反，我们的方法利用地面观测，地面机器人可以轻松观察到这些观测，以获取准确的6自由度外部参数，即使在所有轴线上没有足够的运动的情况下也是如此。最近，提出了一种基于扩展卡尔曼滤波器（EKF）的IMU-LiDAR标定算法，利用平面运动中的GNSS观测模型[7]。然而，它需要额外的GNSS传感器，而我们提出的算法可以在没有额外传感器的情况下标定IMU-LiDAR。

三、系统概述

​ GRIL-Calib的整体系统包括两个主要阶段：预处理和优化，如图2所示。我们的框架受到[20]的启发，第一阶段是预处理阶段，它生成了对接下来的优化阶段至关重要的额外信息。具体而言，预处理阶段执行以下关键任务：

• 通过地面分割进行地面观测，从LiDAR数据中提取地面点，从而便于估计LiDAR传感器相对于地面的相对方向。
• LiDAR测距（LO），利用提取的地面平面并整合提出的地面平面残差，增强LO性能。
• IMU处理，涉及IMU测量的预处理以及使用Madgwick滤波器[21]计算IMU相对于地面的相对方向。
• 数据同步，旨在使用交叉相关方法确定IMU和LiDAR数据之间的近似时间偏移。值得注意的是，此过程与[20]中提出的方法相一致。

​ 第二阶段是优化阶段，旨在利用预处理阶段获取的数据优化外部标定参数。应用三种类型的约束：基于角速度和线性加速度的统一时间-空间约束，以及提出的地面平面运动（GPM）约束。GPM约束确保机器人的运动保持在地面上，并被整合到目标函数中以实现精确的外部标定，同时限制平面运动。与[20]中每种目标函数分别和顺序地优化不同，我们通过为每个目标分配不同的权重值，同时优化所有三种类型的约束。这种方法相比于[20]中的方法可以提高性能。
​ 在全文中，我们使用以下符号：LiDAR坐标系表示为 { L } \{L\} {L}，IMU坐标系表示为${}_I$， $R_L^I\in SO(3)$ 是从IMU坐标系到LiDAR坐标系的旋转矩阵。 $p_L^I\in R^3$ 是从IMU坐标系到LiDAR坐标系的平移向量。 $t_L^I\in R^3$ 是IMU和LiDAR之间的时间偏移。 $b_a，b_g\in R^3$ 分别表示IMU的加速度偏差和角速度偏差。

四、预处理

​ 在预处理阶段，我们获取了一些参数和传感器测量数据，这些将在随后的优化阶段中使用。
A. 通过LiDAR地面分割进行地面观测
​ 首先，我们从LiDAR输入中分割出地面。LiDAR地面分割旨在获得LiDAR相对于地面的旋转矩阵 $R_L^G$ 。当获取当前LiDAR扫描 P 时，使用Patchwork++ [22]（一种最先进的地面分割算法）提取一组地面点 G 。然后，我们对地面点 G 的协方差矩阵 $C_G$ 应用主成分分析（PCA），确定地平面的法向量 $n_L=(a_L,b_L,c_L{)}^T$

$$a_{L}x+b_{L}y+c_{L}z+d_L=0$$

其中， $n_L$ 表示LiDAR坐标系 {L} 中的地面的法向量。我们还定义了一个相对于地面坐标系 {G} 的法向量 $n_G=(0,0,1{)}^T$ 。从这两个法向量 $n_L$ 和 $n_G$ 中，我们通过以下方式获得一个从{G}坐标系到{L}坐标系的旋转矩阵

$R_L^G$：$R_L^G=exp([{\phi }_{GL}{n}_{GL}]\times )$
其中， ${\phi }_{GL}=arccos(n_G^T{n}_L)\in R$ 和 $n_{GL}=n_G\times n_L\in R^3$ 分别表示 {G} 和 {L} 之间的旋转角度和向量。两个单位向量的内积为它们之间的夹角的余弦值，表示旋转角度，两个向量的叉乘为旋转轴。

B. 利用地平面残差的LiDAR测距
我们使用迭代误差状态卡尔曼滤波器（IESKF）来获取LiDAR测距（LO），其过程类似于[20]。然而，我们通过利用地面机器人被限制在二维平面上移动的假设来提高LO的性能。当我们将LiDAR的状态向量 x_k 定义为
$x_k=[log(R_{L_k},p_{L_k},{\omega }_{L_k},v_{L_k}]$ 和其运动如下：
$xk+1=x_k⊞(\Delta t\cdot F(x_k,w_k))$
其中， $F(x_k,w_k)=[\omega L_k,v_{L_k},{\epsilon }_{\omega },{\epsilon }_v]$ ，$R{L}_k$ 表示从初始LiDAR坐标系 $L_0$ 到当前时间 k 的LiDAR坐标系 {L_k} 的姿态，即 $R{L}_k=R^{L_0}{L}_k$ ，$log(\cdot )$表示对数映射。 $p{L}_k=p^{L_0}{L}_k$ 表示当前时间 k 的LiDAR的位置。 $\omega L_k$ 和 $v{L}_k$ 分别表示LiDAR在时间 k 的角速度和线速度。 KaTeX parse error: Undefined control sequence: \[ at position 5: w_k=\̲[̲\varepsilonω,\v… 是由零均值高斯分布表示的随机游走噪声。 Δt 是两次连续扫描 之间的时间间隔，符号 ⊞ 表示在状态流形上封装的“boxplus”操作。
IESKF的预测步骤包括状态预测和协方差传播，如下所示：
${\bar{x}}_{k+1}={\bar{x}}_k⊞(\Delta t\cdot F({\bar{x}}_k,0))$

$P_{k+1}=F_X{P}_k{F}_X^T+F_w{Q}_k{F}_W^T$
其中，(^)(~)(-) 表示预测、误差和最优状态， P_k 和 Q_k 分别是误差状态 X_k 和噪声 w_k 的协方差矩阵，Fx和 Fw分别是 X{k+1}-X_k 相对于 X 和w 的导数在零处的求值。
IESKF的校正步骤通过最大后验（MAP）问题进行，就像[20]中一样，其中先验分布是通过状态预测获得的，似然性是通过点对平面测量模型的一阶近似获得的。
当在时间 k 给出了 P_k={p^{L_k}j∣j=1,⋯,N_k} 时，测量模型 [4] 基于这样的思想构建，即在时间 k 获取的当前点 p^{L_k}_j 应该保持在地图中相应的邻近平面 π_j 上，具体描述如下：

$0=hj(x_k,p_j^{L_k}+{\epsilon }_j^{L_k})=(u_j^{L_0}{)}^T(T_{L_k}^{L_0}(p_j^{L_k}+{\epsilon }_j^{L_k})-q_j^{L_0})$

其中， $u_j^{L_0}$ 是相对于最近的相应平面定义的单位法向量， $T_{L_k}^{L_0}$ 代表LiDAR姿态，点 $q_j^{L_0}$ 是地图中的LiDAR点。 对上式采用一阶近似：

$h_j(x_k,p_j^{L_k}+{\epsilon }_j^{L_k})=h_j(x_k,p_j^{L_k}+0)+H_j{x}_k+v_j=z_j+H_j{x}_k+v_j$

其中， $z_j=h_j(x_k,p_j^{L_k}+0)$ ， $H_j=\frac{\partial h_j}{\partial x_k}$ , $v_j$ 是测量噪声扰动。

​ 与文献【20】不同，我们通过平面约束减少激光里程计漂移，考虑到载体运动限制在2D空间中，可使用横滚角和偏斜角和z轴平移为常值的约束。当已知看k时刻地平面法向量的时候法相俩个应该与地面系的X-Y平面正交：

$[R_L^R{R}_{L_K}(n_{L_K}+{\epsilon }_{n_k}){]}_{1,2}=0$

其中， ${\epsilon }_{n_k}$ 是地面法向量的观测噪声， $[-{]}_{1,2}$ 表示只是用第一、二个向量元素。

​ z轴平移分量相对于地面系的分量应为0：

$e_3{R}_L^{G}L{P}_{L_k}=0$

​ 将上两个零约束合并你，定义地平面测量模型为：

$0=h_{\pi }(x_k,n_{L_k}+{\epsilon }_{n_k})=\left(\frac{[R_L^R{R}_{L_K}(n_{L_K}+{\epsilon }_{n_k}){]}_{1,2}}{e_3{R}_L^{G}L{P}_{L_k}}\right)$

​ 一阶近似后得到：

$0=h_{\pi }(x_k,n_{L_k}+{\epsilon }_{n_k})=h_{\pi }(x_k,n_{L_k}+0)+H_j{x}_k+v_j=z_j+H_j{x}_k+v_{\pi }$

​ 通过将 $h_j$和$h_{\pi }$ 采用MAP估计，得到：

$min(||X_k-{\bar{X}}_k|{|}_{P_k}^2+{\sum }_{j=1}^m||Z_j^{\tau }+H_j^{\tau }{\bar{X}}_k|{|}_{R_k}^2+||Z_{\pi }^{\tau }+H_{\pi }^{\tau }{\bar{X}}_k|{|}_{S_k}^2)$

​ 对上式进行优化求解得到：

L k = { ω L k , v L k , α L k , a L k } L_k=\left\{ \omega_{L_k},v_{L_k},\alpha_{L_k},a_{L_k} \right\} Lk​={ωLk​​,vLk​​,αLk​​,aLk​​}

其中，${\omega }_{L_k}$ 和 $v_{L_k}$ 分别表示LiDAR在时间 k 的角速度和线速度。 ${\alpha }_{L_k},a_{L_k}$ 是角加速度和线加速度，是对${\omega }_{L_k}$和 $v_{L_k}$求导得到的。

C.IMU处理和激光里程计同步

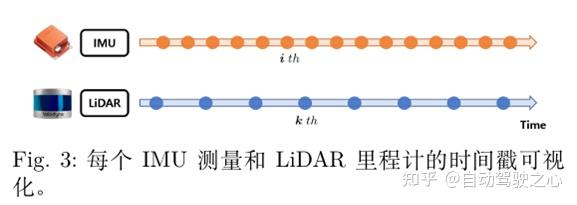
​ IMU测量模型为：

${\bar{\omega }}_i={\omega }_i+b_g+{\epsilon }_g,{\bar{a}}_i=a_i+R_{I_i}^w{g}^w+b_a+{\epsilon }_a$

​ 需要注意的是IMU测量频率远大于雷达里程计，我们分别为IMU和雷达里程计使用两个时间索引i和k，时间戳示意图如图3所示。

​ 与文献【20】相同，我们使用滤波器滤除IMU中的随机噪声 ${\epsilon }_g$和${\epsilon }_a$ ,并将IMU输出降采样到与雷达同频：

${\bar{\omega }}_{I_k}={\omega }_{I_k}+b_g,{\bar{a}}_{I_k}=a_{I_k}+R_{I_k}^w{g}^w+b_a$

​ 为了实现精确的同步，采用了粗到细的方式估计时间偏差 t^I_L ，与文献[20]相同，时间偏差由粗偏差和细偏差组曾，通过交叉关联方法计算粗估计时间偏差：

$t_c^{\ast }=argmax{\sum }_a^b||{\bar{\omega }}_{I_{k+t_c}}||\cdot ||{\omega }_{L_k}||$

​ 细时间偏差在下一节中细化，作为优化过程结果输出。通过使用Madgwick滤波器处理IMU测量，估计地面坐标系到IMU坐标系的旋转矩阵 $R_I^G$ 。最后输出：

$I_k=\left\{{\bar{\omega }}_{I_k},{\bar{\alpha }}_{I_k},{\bar{a}}_{I_k},R_I^G\right\}$

五、通过流形优化估计外参

​ 使用第四节B和C小节输出的 L_k和I_k ,将IMU和激光雷达外参估计构建为优化问题，标定参数为：

$x_{cal}=[R_L^I,p_L^I,t_f,b_g,b_a]$

A.时空约束

​ 联合优化文献[20]中的两约束，第一个约束使用IMU和LO的角速度测量构建：

${\omega }_{I_k^{\prime }}+t_f\cdot {\bar{\alpha }}_{I_k^{\prime }}={R_L^I}^T{\omega }_{L_k}+b_g$

​ 通过补偿时间偏差并假设IMU角加速度为常量，得到：

$r_w(R_L^I,b_g,t_f)={R_L^I}^T{\omega }_{L_k}+b_g-{\omega }_{I_k^{\prime }}-t_f\cdot {\bar{\alpha }}_{I_k^{\prime }}$

​ 第二个约束使用IMU和LO的线加速度测量构建：

$R_L^I{\bar{a}}_I=a_L+\left\{([{\omega }_{L_k}{]}_{\times }^2+[alph{a}_L{]}_{\times }^2)\cdot p_L^I\right\}$

​ 可以得到约束：

$r_w(R_L^I,p_L^I,b_a)=R_L^I({\bar{a}}_{I_k}-b_a)-a_L-\left\{([{\omega }_{L_k}{]}_{\times }^2+[{\alpha }_L{]}_{\times }^2)\cdot p_L^I\right\}$

B.地面运动约束（GPM）

​ 本节提出的地面运动约束与文献【13】中的约束相似，使用平面运动信息提升VINS的精度。然而文献【13】是用于运动估计，本文中用来标定外参。在GOM中参数化 R^I_L,pI_L ，直接测量IMU到地面的高度并作为先验知识 d_I ，利用平移外参由于垂直于运动平面而在z轴不客观的事实，基于地面和两个传感器旋转参数约束得到：

${\left[R_I^G{R}_L^I{R}_G^L{e}_3\right]}_{1,2}$

$e_3^T(R_L^I{R}_G^L{d}_I-R_G^L{d}_L)=e_3^T{p}_L^I$

​ 写成残差形式：

$r_g(R_L^I,p_L^I)=\left(\frac{{\left[R_I^G{R}_L^I{R}_G^L{e}_3\right]}_{1,2}}{e_3^T(R_L^I{R}_G^L{d}_I-R_G^L{d}_L)-e_3^T{p}_L^I}\right)$

​ 本文Gril-Calib通过地平面运动约束实现在平面运动下在不客观方向下的外参标定。

C.单优化过程

​ 文献[20]用两个分开的约束 r_w 和 r_a ，双阶段优化外参。首先，通过最小化r_w计算旋转外参，然后最小化r_a计算平移外参。然而，双阶段方法忽略了这两个约束之间的关联性，比如说r_a与旋转和平移外参都有关。本文算中，通过将两约束构建为一个优化问题，优化目标函数为：

$x_{cal}^{\ast }=argmin\sum \left\{{\rho }_w||r_w(R_L^I,b_g,t_f)|{|}_{{\sum }_{r_w}}^2+{\rho }_a||r_w(R_L^I,p_L^I,b_a)|{|}_{{\sum }_{r_a}}^2+{\rho }_g||r_g(R_L^I,p_L^I)|{|}_{{\sum }_{r_g}}^2\right\}$

​ 通过最小化目标函数同时优化三个残差，残差下标表示马氏距离协方差矩阵，系数为柯西核函数。

六、实验

A. 实验设置

​ 我们的实现基于 C++，在 Ubuntu 18.04 上使用 ROS （机器人操作系统）。我们使用 4 核 Intel® Core™ i5-6600 CPU 和 Titan XP GPU 进行实验。我们使用 Ceres-solver 2 来计算非线性优化。我们使用三个公共数据集评估了这 些算法：M2DGR 、Hilti 和 S3E，涵盖了室内和室外环境。按照 [20] 中使用的评估方案，我们仅根据 RMSE（均方根误差）评估空间外在标定参数，跳过了对时间偏移 t^I_L 的评估。为了证明我们 的 Gril-Calib 的有效性，我们将我们的方法与其他最近 的 IMU-LiDAR 校准方法进行了比较，如 ILC [18] ，FAST-LIO2 [4] ，OA-LICalib [11] ，LI-Init [20] 。所有算法都在同一环境中重现。

B. M2DGR上的外部校准性能

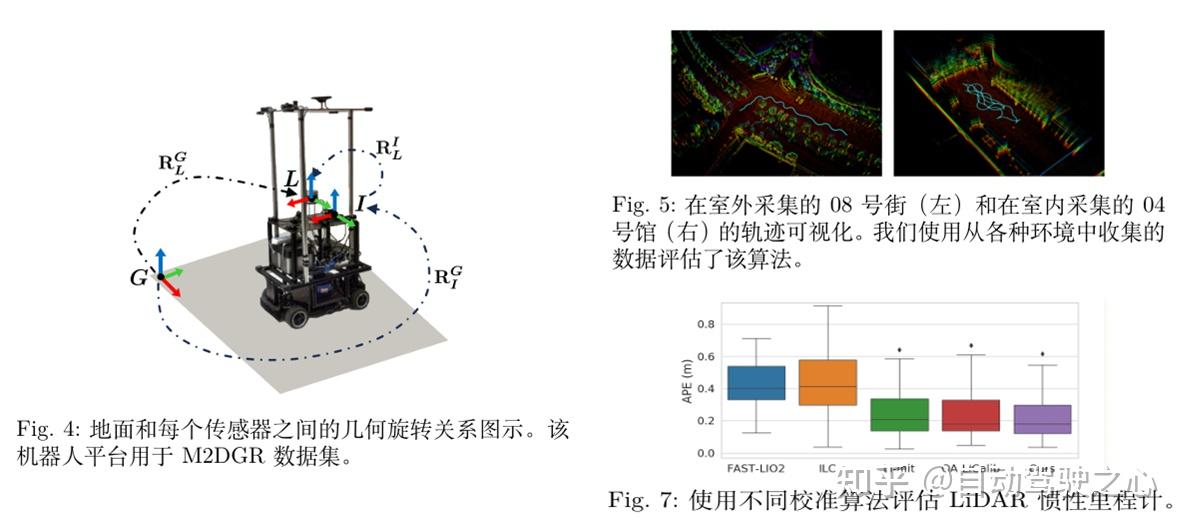
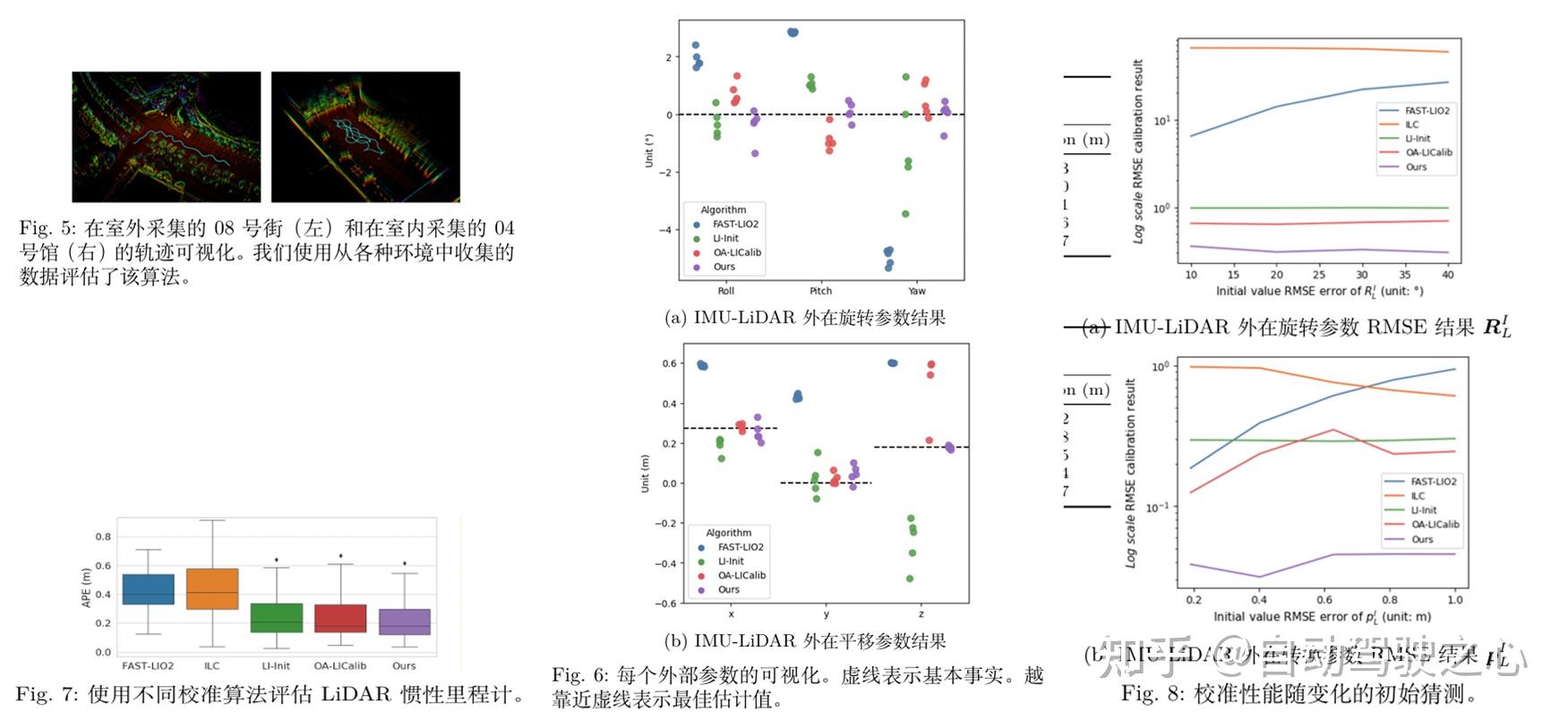
​ 表I总结了 M2DGR 数据集上的校准结果。M2DGR 使用 Velodyne VLP-32C 作为 LiDAR，使用 Handsfree A9 作为 IMU。为了保持一致的比较，所有算法的初始旋转和平移参数都设置为相同。初始旋转参数设置为(−5.0,−5.0, 5.0)°。初始平移参数偏离基于 RMSE 的地面实况 0.402 米，大小为 (0.6, 0.45, 0.6)m。我们将所有剩余的状态向量 tf , bg, ba 初始化为零。数据是从室内（Hall 04 和 Lift 04）和室外（Gate 01 、Rotation 02 和 Street 08 ）收集的，部分可视化如图 5 所 示。表 I总结了 M2DGR 上的校准结果。该表显示，本文 Gril-Calib 明显优于其他竞争方法，特别是与基线 [20]的 LI-Init相比，旋转的 RMSE 降低了 75 %，平移的 RMSE 降低了79 %。

​ 每种标定方法的外部参数如图6所示。图6a 和图6b分别是旋转矩阵和平移矩阵的结果。在这两个图 中，虚线表示外在参数的基本事实。因此，越接近虚线， 校准方法越好。图中没有显示之外ICL ，因为它的误差明显大于其他方法。

C. 其他的外在校准性能

​ S3E 和 HILTI 数据用作附加数据集，这两个数据集都是在室内捕获的。S3E 数据集使用 Velodyne VLP-16 和 Xsens MTi 30 IMU，而HILTI 数据集使用 Ouster OS0-64 LiDAR 和 AlphaSense IMU。其结果分别总结在表 II和表 III，我们的算法优于其他竞争方法，它显示了本文 Gril-Calib 在各种机器人平台上的可靠准确性。我们还观察到，表 III 中基线 3 序列中的内存计算问题，OA-LICalib 在校准中失败。可能是由于 OA-LICalib 使用 surfel 映射进行校准，计算成本随着 surfel 的数量而迅速增加。相比之下，我们的算法运行流畅，没有任何内存问题。

D. 对初始猜测的鲁棒性

​ 外部校准通常需要初始参数值，并且他显着影响标定结果 。我们改变初始参数进行多次实验，测试不同标定方法对初始参数的鲁棒性。使用M2DGR 中的Gate 01 序列。结果如图8所示。图 8a显示了在 固定初始平移外参但更改旋转外参 时校准误差的变化。图 8b是 固定初始旋转外参但更改平移外参时的结果。有趣的是，OA-LICalib 在前三个数据集中表现出相对较好的性能，但随着初始猜测的增加，其准确性迅速下降。相反，LI-Init 表现出 与最初猜测相反的强大性能，但由于平面运动有限，不如本文 Gril-Calib 准确。

E. 应用于 IMU-LiDAR 融合系统

​ 我们通过将各算法的结果应用于 IMU-LiDAR 融合系统并评估相应的里程计精度来比较竞争的外部校准方法。 在实验中，我们利用 Faster-LIO 作为 IMU-LiDAR 融 合系统。使用 hall 02 序列（该序列未在第VI-B小节中用过）。在图7 中描述了不同校准方 法的绝对位姿误差（APE）。可以看出， Gril-Calib 获得的里程计优于其他方法。特别是， Gril-Calib 比　LI-Init 提高了 8.6 %，比 OA-LICalib 提高了 9.6 %。同时该实验表明，IMU-LiDAR 融合SLAM时标定的重要性。

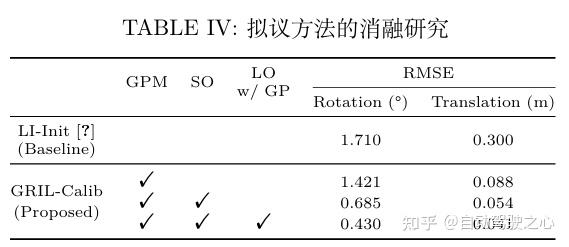
F. 消融研究

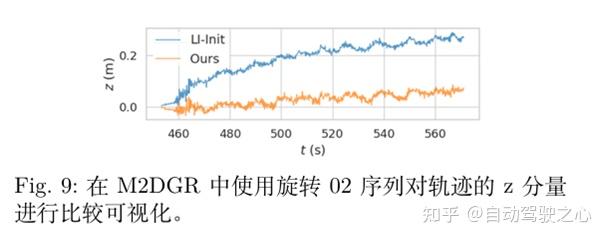
​ 进行三个关键模块的消融实验，将结果与基线 [20] 的结果进行比较，如表IV所示。在表格第一行，“GPM”、“SO”和“LO w/ GP”表示我们论文中所做的三项贡献：“使用 GPM 约束的外参标定”、“单次优化标定”和“地平面残差的LO”。表中显示，有SO 比无SO平移外参的 RMSE 降低 34 %，表明旋转外参和平移外参是高度相关的，忽略相关性的分阶段优化会导致精度下降。如图 9 所示，有地面约束的LO比没有地面约束的LO，z 轴漂移有效减少 ，这种漂移的降低导致了更稳定和准确的测量，从而提高了我们校准方法的整体精度。

七、结论

​ 在本文中，我们提出了一种针对地面机器人的新型无目标 IMU-LiDAR 外部标定框架GRIL-Calib。为了解决机器人在平面运动时计算准确的6-DoF 外参可观性差的问题，提出了地面观测的地面运动 （GPM）约束。将校准问题表述为单一优化（SO）问题，保留多个残差的相关性。 此外，我们提出了地平面残差函数来减少 LiDAR 里程计 的 z 轴漂移，提升LO的精度，从而间接提高校准的准确性。最后，我们将 GRIL-Calib 应用于三个公共数据集并改变一些初始校准参数来验证算法性能。我们承认，我们的算法的性能可能会受到不平坦地面的影响，未来的工作应侧重于此类地形的校准。