一、协方差矩阵
1.协方差定义

2.R语言实现
#协方差矩阵
#等价于cov(data)
data<-as.matrix(data)
n<-nrow(data)
mx<-diag(1,n)-matrix(1,n,n)/n
covA<-t(data)%*%mx%*%data/(n-1);covA
3.可视化运算
假设有X、Y两个矩阵,分别求X的协方差、Y的协方差、X和Y的协方差。
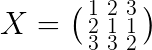
第一步先求X的每一列的均值:
第二步计算
,每列减去每列相应的均值:
第三步乘积求和:
同理可得Y的协方差:
求X和Y的协方差,先求
:
再乘积求和,用X的每一列乘以Y的每一列的转置:
二、相关系数矩阵
1.相关系数定义

2.R语言实现
#相关系数矩阵
#等价于cor(data)
corA<-covA
for(j in 1:n )
{
for(k in 1:n)
{
corA[j,k]<-covA[j,k]/(sqrt(covA[j,j])*sqrt(covA[k,k]))
}
}
corA
3.可视化运算
根据前面所求协方差:

按照公式可求得:

相关资料:数据分析与R软件第二版(李素兰著)每章例题代码和数据,下载地址:https://download.csdn.net/download/lph188/10802159









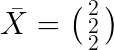



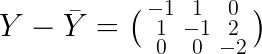

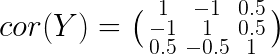
















 1941
1941

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








