【C# / Algorithm】任意圆形和三角形相交部分面积的计算方法

    采用运算符重载技术，设计一个名为"&"的运算符，使用该运算符可以计算出一个圆与一个三角形的公共部分的面积，并给出示例代码。已知数据：圆的圆心坐标和半径，三角形的三个顶点坐标。

今天无意中在贴吧发现了这样一道题，很显然难点在后半题。

于是开始考虑圆形和三角形的相交面积计算的通用方法。

我的思路：

三角形和圆形相交的情况比较多，按交点数就有0到6个，每种情况还有很多不同的细分情况要考虑。
将圆形所在的正方形，无限细分成NxN的小矩形(像素点?)，然后一次判断每个矩形是否即在圆形内又在三角形内，则该矩形为相交部分。
统计所有的矩形，则可以求出相交部分的近似面积。
如果分割的足够细，则结果精度会比较高。

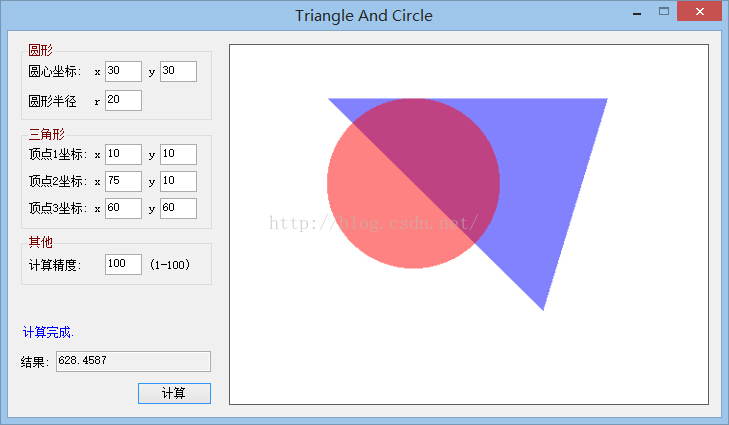
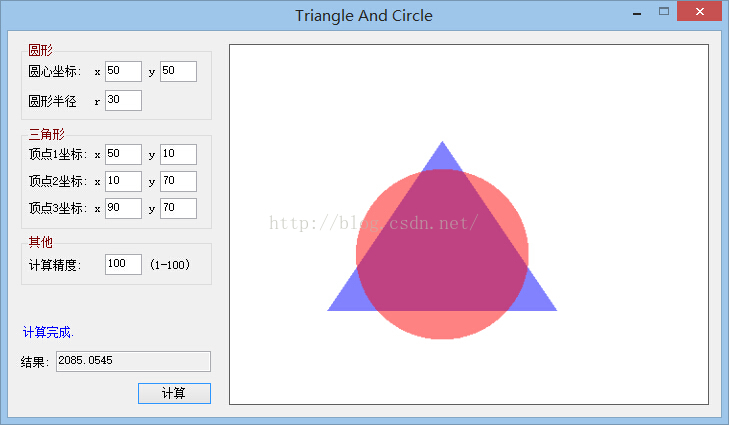
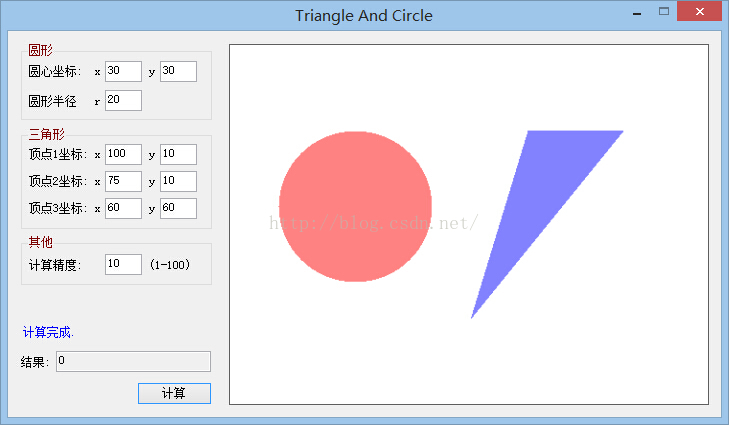
测试Demo截图：

以下是算法核心代码（不包含winform界面代码）

using System;
using System.Collections.Generic;
using System.Text;
using System.Drawing;

namespace CrossArea
{
    /// <summary>
    /// 面积计算
    /// </summary>
    public static class Area
    {
        /// <summary>
        /// 计算交叉部分面积
        /// </summary>
        /// <param name="p">圆心坐标</param>
        /// <param name="r">圆半径</param>
        /// <param name="a">三角形A点坐标</param>
        /// <param name="b">三角形B点坐标</param>
        /// <param name="c">三角形C点坐标</param>
        /// <param name="accuracy">计算精度</param>
        /// <returns></returns>
        public static double CrossArea(PointF p, float r, PointF a, PointF b, PointF c, float accuracy)
        {
            // 计算缩放精度
            p = new PointF(p.X * accuracy, p.Y * accuracy);
            r = r * accuracy;
            a = new PointF(a.X * accuracy, a.Y * accuracy);
            b = new PointF(b.X * accuracy, b.Y * accuracy);
            c = new PointF(c.X * accuracy, c.Y * accuracy);
            // 扫描起点
            PointF p_start = new PointF(p.X - r, p.Y - r);
            // 扫描终点
            PointF p_end = new PointF(p.X + r, p.Y + r);
            // 扫描统计
            double count = 0;
            // 扫描圆形所在的正方形内所有的点
            for (int i = (int)p_start.X; i <= (int)p_end.X; i++)
            {
                for (int j = (int)p_start.Y; j <= (int)p_end.Y; j++)
                {
                    Point pt = new Point(i,j);
                    // 如果扫描当前点在圆形和三角形内
                    if (IsInCircle(p, r, pt) && IsInTriangle(a, b, c, pt))
                    {
                        count++;
                    }
                }
            }
            // 计算结果
            double answer = count / (accuracy * accuracy);
            return answer;
        }

        /// <summary>
        /// 计算点到点的距离
        /// </summary>
        /// <param name="point1">点1</param>
        /// <param name="point2">点2</param>
        /// <returns>距离</returns>
        public static double LengthFromPointToPoint(PointF point1, PointF point2)
        {
            return Math.Sqrt(Math.Pow(point1.X - point2.X, 2) + Math.Pow(point1.Y - point2.Y, 2));
        }          

        /// <summary>
        /// 点T是否在圆P内
        /// </summary>
        /// <param name="p">圆心坐标</param>
        /// <param name="r">圆形半径</param>
        /// <param name="t">点T</param>
        /// <returns></returns>
        public static bool IsInCircle(PointF p, float r, PointF t)
        {
            float length = (float)LengthFromPointToPoint(p, t);
            if (length <= r)
                return true;
            else
                return false;
        }

        /// <summary>
        /// 点T是否在三角形内
        /// </summary>
        /// <param name="a">三角形A点坐标</param>
        /// <param name="b">三角形B点坐标</param>
        /// <param name="c">三角形C点坐标</param>
        /// <param name="t">点T</param>
        /// <returns></returns>
        public static bool IsInTriangle(PointF a, PointF b, PointF c, PointF t)
        {
            bool temp1 = IsInIntercept(a, b, c, t);
            bool temp2 = IsInIntercept(a, c, b, t);
            bool temp3 = IsInIntercept(b, c, a, t);
            if (temp1 && temp2 && temp3) return true;
            else return false;
        }

        /// <summary>
        /// 点T是否在线AB和C的截距范围内
        /// </summary>
        /// <param name="a">线端点A</param>
        /// <param name="b">线端点B</param>
        /// <param name="c">三角形的另一个点C</param>
        /// <param name="t">点T</param>
        /// <returns></returns>
        public static bool IsInIntercept(PointF a, PointF b, PointF c, PointF t)
        {
            // AB延长线在Y轴上的截点，AB过C和T平行线在坐标轴上的截点
            float p1, p2, pt;
            // 斜率不存在时
            if (a.X == b.X)
            {
                p1 = a.X;
                p2 = c.X;
                pt = t.X;
            }
            else
            {
                // 斜率为0时
                if (a.Y == b.Y)
                {
                    p1 = a.Y;
                    p2 = c.Y;
                    pt = t.Y;
                }
                // 斜率不为0时
                else
                {
                    // 斜率
                    float k = (a.Y - b.Y) / (a.X - b.X);    
                    float bb = a.Y - k * a.X;
                    // Y轴的截距
                    p1 = bb;
                    p2 = c.Y - k * c.X;
                    pt = t.Y - k * t.X;
                }
            }
            if ((pt <= p2 && pt >= p1) || (pt <= p1 && pt >= p2)) return true;
            else return false;
        }
    }
}