一个逻辑问题的分析：“天堂与地狱的守卫”

最近和朋友讨论一个逻辑问题，据说也是个以前出现过的面试题了。拿出来和大家分享。

问题如下：

你来到两道门口，一道是天堂之门， 一道是地狱之门 。
门口都有一个守卫，只知道守卫一个只说假话，一个只说真话。
现在你只有一次提问机会，只向一个守卫问一个问题，这个守卫对你的问题，只给出“是”或者”不是“的答案。（对于无法给出是非的问题，守卫会直接把你砍死。。。）
请问怎么问才能准确进入天堂之门？

我们将守卫守门的所有情况列成如下的一个矩阵：

守卫分两种情况，第一行代表天堂守卫是诚实的情况，第二行分为天堂守卫为说谎话的情况。

而每种情况你都有2个可能，要么问到真话守卫，要么问到假话守卫。因此问题的解空间是一个2*2的矩阵。

这个问题难在，不管你问“ 你是说真话的吗？”还是问“ 你守卫的门是天堂的吗？”，都无法得到满意信息。

如下图，如果你问“ 你守卫的门是天堂的吗？”，所有的情况如下图所示：

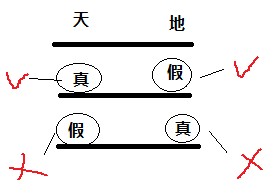
红色的勾表示如果你问这个守卫（勾连接的那个画圈的守卫）问题，他会说“是”。”叉“表示说”否“。

看到这个图你就明白为什么问不出答案了。因为无论是上下哪种情况，天堂的守卫既有可能说”是“，也有可能说”不是“。

解法1：通过解空间反求问题x

我们的目的是找出天堂之门。也就是说，需要设计一个问题， 将解空间按照天堂和地狱来进行分离。

也就是说，我们需要设计一个问题，将解空间分解为如下情况：

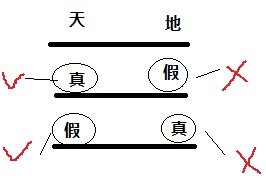
这样解空间按照天堂和地狱分开了。只要回答是”是“，该守卫就是天堂守卫。反之就是地狱守卫。

如何寻找这样的问题呢？

容易知道，为得到天堂地狱相关的信息，我们问的问题一定是 描述当前守卫守门状况的一个描述。（例如你问1+1=2吗，真话守卫说是，假话守卫说否，这样只能区分出守卫真假，但是无法区分天堂和地狱）

如果我们把这个状态当做函数的输入x，守卫对该问题的回答的解空间当做y，那么这个函数可以写作：

Y = f(X)

由于y和x是2*2的矩阵。那么可把上式写成：

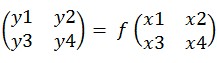
那么f函数执行的是什么操作呢？

我们知道，x表示的是 一个描述在四种守卫情况中的真值表，真值表是客观存在的，所以一定是为真的。真话守卫不会修改这个真值，而谎话守卫一定会给出相反结果。那么，这个 f可以表示为：

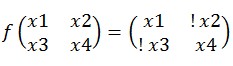
由于f只做了反转操作，显然 f操作是可逆的。

要让天堂守卫都说”是“，地狱守卫都说”否“，就是说y应该是：y1=y3=1, y2=y4=0。

既然我们已经知道我们需要什么样的y了。因此，已知 y反求 x，如下：

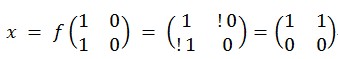
这个x就是我们可以拿出来问守卫的问题。

还记得我们对矩阵的定义吗？

因此，把上面的x代入该矩阵定义，得到如下的 守卫状态：

守天堂的是真话守卫；    守地狱的是假话守卫；

守天堂的不是假话守卫；守地狱的不是真话守卫；

这实际上是一个状态的四个等价描述的。因此，这个状态就是满足输出y的问题x。

因此，只要向任意一个守卫问上面的任意一个问题即可。只要回答是”是“，该守卫就是天堂守卫。反之就是地狱守卫。

解法2：构造高阶逻辑表达式

假设说真话的守卫对问题的回答为f=T(x),假话的为f=F(x),那么有：

T(0) = 0, T(1) = 1;

F(0) = 1, F(1) = 0;

注意到：

T(F(0)) = 1; T(F(1))=0;

F(T(0)) = 1; F(T(1))=0;

这说明通过一个问题x经过F和T的两次加工，最后的答案是一样的也即

T(F(x)) = F(T(x)) = !x

因此，我们可以构造如下问题：

” 另外那个守卫会告诉我你是天堂守卫吗？“

得到的回答一定和”你是天堂守卫“相反。也就是说，他说”是“，那他就是地狱守卫；他说不是，那他就是天堂守卫。