为了解决特定问题而进行的学习是提高效率的最佳途径。这种方法能够使我们专注于最相关的知识和技能,从而更快地掌握解决问题所需的能力。
(以下练习题来源于《统计学—基于Python》。联系获取完整数据和Python源代码文件。)
练习题
一家牛奶公司有4台机器装填牛奶,每桶的容量为4L。下面是从4台机器中抽取的装填量样本数据(单位:L):
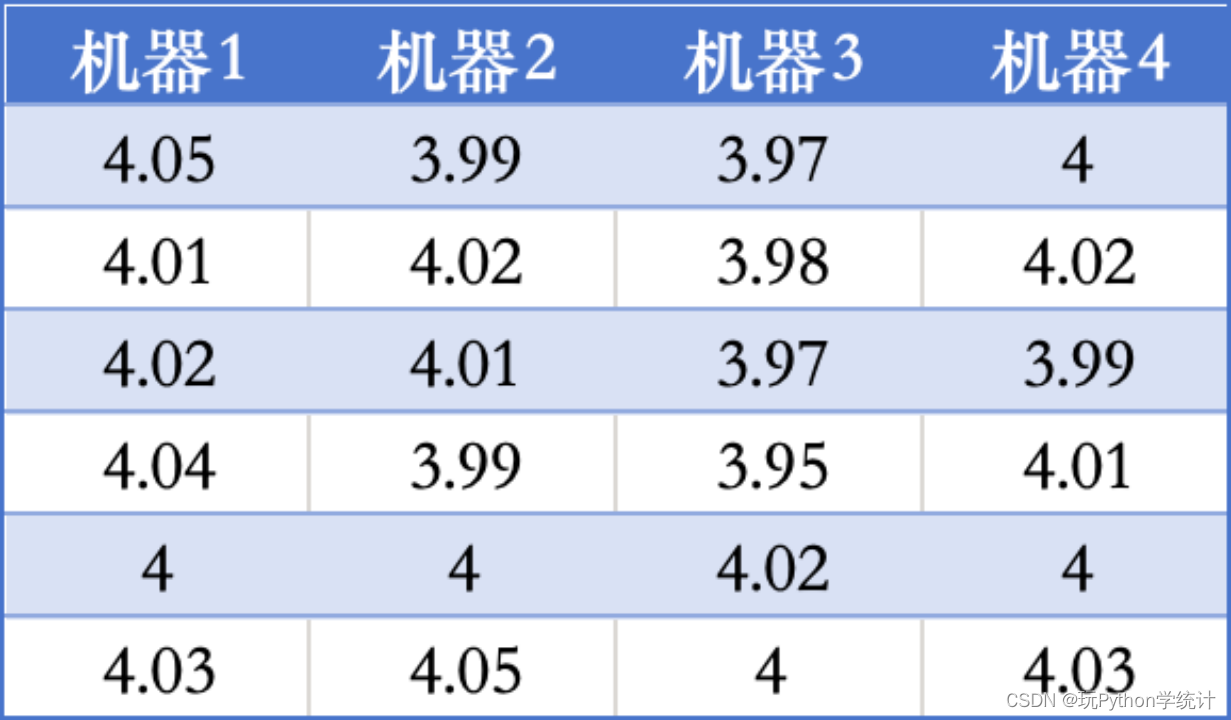
(1)检验机器对装填量是否有显著影响(α=0.05)。
(2)分析效应量。
(3)采用HSD方法比较哪些机器的装填量之间存在显著差异。
(4)检验装填量是否满足正态性和方差齐性。
分析与结果
(1)题分析与结果
设机器种类对装填量的效应分别为α1(机器1)、α2(机器2)、α3(机器3)、α4(机器4)。提出的假设为:
H0:α1=α2=α3=α4(机器种类对装填量的影响不显著);H1:α1,α2,α3,α4至少有一个不等于0(机器种类对装填量的影响显著)
通过Python进行方差分析,结果显示,p值=0.013485,小于0.05,因此拒绝H0,接受H1,即在显著性水平为0.05的情况下,我们有理由相信机器种类对装填量有显著影响。
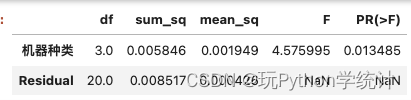
Python代码
import pandas as pd
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
exercise9_1 = pd.read_csv('exercise9_1.csv')
# exercise9_1.head()
# 将短格式数据融合成长格式数据,并另存为 exercise9_1_1
exercise9_1_1 = pd.melt(exercise9_1, value_vars = ['机器1', '机器2', '机器3', '机器4'],\
var_name = '机器种类', value_name = '装填量') # 融合数据
# exercise9_1_1.head()
# 拟合单因子方差分析模型并输出方差分析表
model1 = ols(formula = '装填量 ~ 机器种类', data = exercise9_1_1).fit() # 拟合方差分析模型
anova_lm(model1, typ = 1)(2)题分析与结果
使用summary()函数输出模型摘要。效应量即R-squared为0.407,表示装填量取值的总误差中被机器种类解释的比例为40.7%。
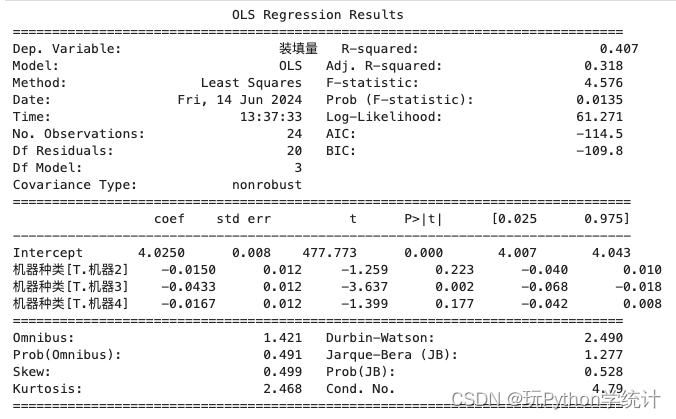
Python代码
# 使用 summary 函数输出模型摘要
print(model1.summary())(3)题分析与结果
根据HSD方法计算结果的p值,可以发现机器1和机器3之间的差异显著,其他机器种类之间差异不显著。
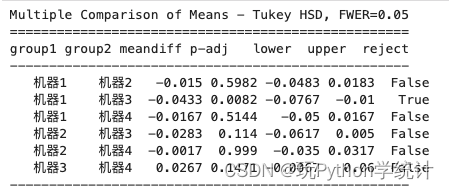
Python代码
# 多重比较
from statsmodels.stats.multicomp import MultiComparison
mc = MultiComparison(exercise9_1_1['装填量'], groups = exercise9_1_1['机器种类'])
print(mc.tukeyhsd(alpha = 0.05))(4)题分析与结果
正态性检验
正态性(normality)假定要求每个处理所对应的总体都服从正态分布,即对于任意一个处理,其观测值是来自正态总体的简单随机样本。在本题中,要求每个机器种类的装填量服从正态分布。
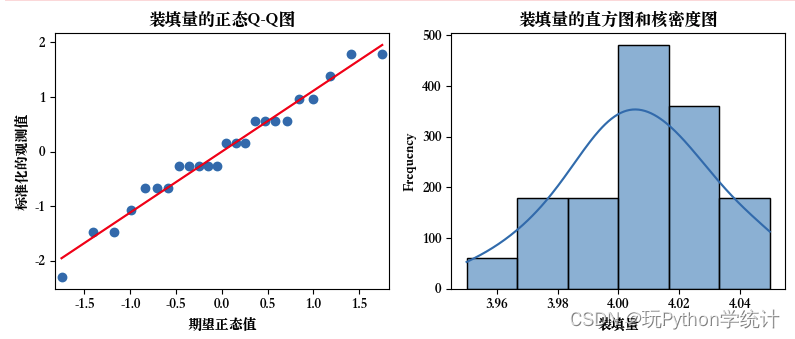
Q-Q图
首先,绘制正态概率图Q-Q图来检验装填量是否服从正态分布。当每个处理的样本量足够大时,可以对每个样本绘制Q-Q图来检验每个处理对应的总体是否服从正态分布;当每个处理的样本量较小时,正态概率图中的点很好,提供的正态性信息有限,这时可以将每个处理的样本数据合并绘制一幅正态概率图来检验正态性。由于本题中每个样本只有6个数据,因此将4个样本数据合并后绘制Q-Q图。
正态Q-Q图显示,装填量近似服从正态分布;直方图与核密度图显示,装填量接近对称分布。
Python代码
# 正态性检验:4种机器类型的装填量数据合并后的正态Q-Q图、直方图即核密度曲线
import pandas as pd
from matplotlib import pyplot as plt
import statsmodels.api as sm
import seaborn as sns
plt.rcParams['font.sans-serif'] = ['Songti SC'] # 设置中文字体
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
exercise9_1 = pd.read_csv('exercise9_1.csv')
# exercise9_1.head()
# 将短格式数据融合成长格式数据,并另存为 exercise9_1_1
exercise9_1_1 = pd.melt(exercise9_1, value_vars = ['机器1', '机器2', '机器3', '机器4'],\
var_name = '机器种类', value_name = '装填量') # 融合数据
# 绘制Q-Q图,采用的数据是 exercise9_1_1
plt.subplots(1, 2, figsize = (8, 3.5))
ax1 = plt.subplot(121)
pplot = sm.ProbPlot(exercise9_1_1['装填量'], fit = True)
pplot.qqplot(line = 'r', ax = ax1, xlabel = '期望正态值', ylabel = '标准化的观测值')
ax1.set_title('装填量的正态Q-Q图', fontsize = 12)
# 绘制直方图和核密度图
plt.subplot(122)
sns.histplot(exercise9_1_1['装填量'], kde = True, bins = 6, stat = 'frequency')
plt.title('装填量的直方图和核密度图')
plt.tight_layout()S-W检验
采用S-W检验或K-S检验来分析。S-W检验的结果如下。4种机器类型的P值均大于0.05,没有证据显示它们的装填量不服从正态分布,即可以认为不同机器对应的装填量均近似服从正态分布。
机器1:统计量W1 = 0.981889, P1 = 0.9606
机器2:统计量W2 = 0.881809, P2 = 0.2775
机器3:统计量W3 = 0.956686, P3 = 0.7939
机器4:统计量W4 = 0.958012, P4 = 0.8043
# 4种机器种类的装填量的S-W正态性检验。
import pandas as pd
from scipy.stats import shapiro
exercise9_1 = pd.read_csv('exercise9_1.csv')
# exercise9_1.head()
# 注意:这里的数据不需要合并,用回原来的数据格式 exercise9_1
x1 = exercise9_1['机器1']
x2 = exercise9_1['机器2']
x3 = exercise9_1['机器3']
x4 = exercise9_1['机器4']
W1, p1_value = shapiro(x1)
W2, p2_value = shapiro(x2)
W3, p3_value = shapiro(x3)
W4, p4_value = shapiro(x4)
print(f"机器1:统计量W1 = {W1:5f}, P1 = {p1_value:.4g}",'\n'
f"机器2:统计量W2 = {W2:5f}, P2 = {p2_value:.4g}",'\n'
f"机器3:统计量W3 = {W3:5f}, P3 = {p3_value:.4g}",'\n'
f"机器4:统计量W4 = {W4:5f}, P4 = {p4_value:.4g}")方差齐性检验
方差齐性(homogeneity of variance)假定要求各处理的总体方差必须相等。对于本题来说,要求每种机器类型的装填量的方差都相等。检验方差齐性可以使用图示法,也可以使用标准的统计检验。
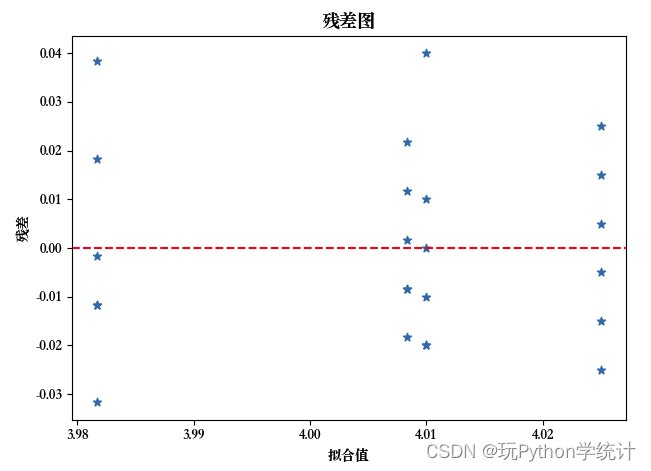
图示法
图示法可采用残差图和箱线图,本题用残差图做展示。残差没有离群点,拟合值和残差的散点随机分布在一个水平带内,其离散程度也基本相同,表明方差分析满足方差齐性。
Python代码
# 用残差图检验方差齐性
import pandas as pd
from statsmodels.formula.api import ols
import statsmodels.api as sm
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['Songti SC'] # 设置中文字体
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
exercise9_1 = pd.read_csv('exercise9_1.csv')
# exercise9_1.head()
# 将短格式数据融合成长格式数据,并另存为 exercise9_1_1
exercise9_1_1 = pd.melt(exercise9_1, value_vars = ['机器1', '机器2', '机器3', '机器4'],\
var_name = '机器种类', value_name = '装填量') # 融合数据
model = ols(formula = '装填量 ~ 机器种类', data = exercise9_1_1).fit() # 拟合单因子模型
# 绘制单因子方差分析的残差图
plt.scatter(model1.fittedvalues, model.resid, marker = '*')
plt.xlabel('拟合值')
plt.ylabel('残差')
plt.title('残差图', fontsize = 13)
plt.axhline(0, ls = '--', color = 'red')
plt.tight_layout()Levene检验法
针对于本题,还采用Levene检验法检验样本数据的方差齐性。计算结果为:统计量F = 0.30864, p值 = 0.81886。由于p值大于显著性水平0.05,不能拒绝原假设(总体方差相等),因此可以认为满足方差齐性。
Python代码
# 用Levene检验法检验样本数据的方差齐性
import pandas as pd
from scipy.stats import levene
exercise9_1 = pd.read_csv('exercise9_1.csv')
sample1 = exercise9_1['机器1']
sample2 = exercise9_1['机器2']
sample3 = exercise9_1['机器3']
sample4 = exercise9_1['机器4']
F, p_value = levene(sample1, sample2, sample3, sample4)
print(f"统计量F = {F:.5f}, p值 = {p_value:.5g}")都读到这里了,不妨关注、点赞一下吧!






















 2086
2086











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








