【地图学】高斯-克吕格（Gauss-Kruger）投影原理、应用详解（3°带、6°带）

一、高斯克吕格投影概述

---

德国数学家、物理学家、天文学家高斯于19 世纪20 年代拟定，后经德国大地测量学家克吕格于1912 年对投影公式加以补充，故称为高斯-克吕格投影（Gauss-Kruger，简称GK），又名"等角横切椭圆柱投影”。中央经线和赤道投影为相互垂直的直线，其它经线均为对称于中央经线、并收敛于两极的凹向曲线；纬线为对称于赤道并弯向两极的凸形曲线，经纬线呈直角相交。

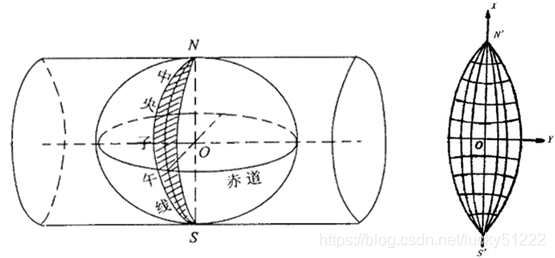
二、高斯---克吕格投影的特点

---

1. 中央经线上没任何变形；

2. 除中央经线上的长度比为1外，其他任何点上长度比均大于1；