图像增强基础：直方图均衡化与自适应直方图均衡化

置顶罗飞居

已于 2025-08-21 12:16:45 修改

阅读量1.9k

点赞数 63

CC 4.0 BY-SA版权

分类专栏：基于OpenCV的图像处理实战文章标签：计算机视觉图像处理 opencv

于 2025-08-19 16:33:23 首次发布

本文链接：https://blog.csdn.net/luofeiju/article/details/150518374

基于OpenCV的图像处理实战专栏收录该内容

9 篇文章

订阅专栏

为什么需要直方图均衡化

在日常拍摄和专业应用中，我们常常会遇到一些“灰蒙蒙”的图像：比如在光线不足的夜景照片、对比度较低的医学影像、甚至是遥感卫星图像。此类图像往往存在灰度分布不均、整体亮度偏低或偏高的问题，导致细节淹没在阴影或高光区域中，难以被人眼或计算机视觉算法有效识别。

为了改善这种情况，众多图像增强技术应运而生。其中，直方图均衡化（Histogram Equalization） 是一种经典方法，它通过调整像素的灰度分布来提升图像的整体对比度，使得视觉效果更加清晰。然而在某些情况下，单纯的全局均衡化并不总是理想，它可能在局部区域引入过度增强或噪声放大的问题。为此，人们提出了 CLAHE（Contrast Limited Adaptive Histogram Equalization，对比度受限自适应直方图均衡化）。它在局部区域进行均衡化处理，并引入对比度限制机制，从而在增强细节的同时有效抑制噪声。

本文将从理论原理出发，系统介绍直方图均衡化与 CLAHE 的基本思想、数学推导与优缺点，并结合 OpenCV 实现，展示它们在实际图像处理中的效果与应用场景。

什么是直方图

在理解直方图均衡化之前，我们首先需要理解直方图。一幅灰度图像可以看作是由大量像素点组成的，每个像素都有一个灰度值（通常在 0～255 之间）。直方图就是统计图像中 每个灰度级出现的次数或概率，并以柱状图的形式展示。

横轴：灰度值（0 表示黑色，255 表示白色）。
纵轴：该灰度值对应的像素数量（或概率）。

公式表示为 $h(k)=n_{k}, k = 0, 1,...,L-1$ ，其中：

$L$ 是灰度级数（8 位图像中 $L=256$ ）；
$n_{k}$ 表示灰度值为 $k$ 的像素个数；
若将其归一化，可以得到概率分布： $p(k)=\frac{n_{k}}{N}$ ， $N$ 为图像总像素数。

下图是一张灰度图像与其对应的归一化灰度直方图

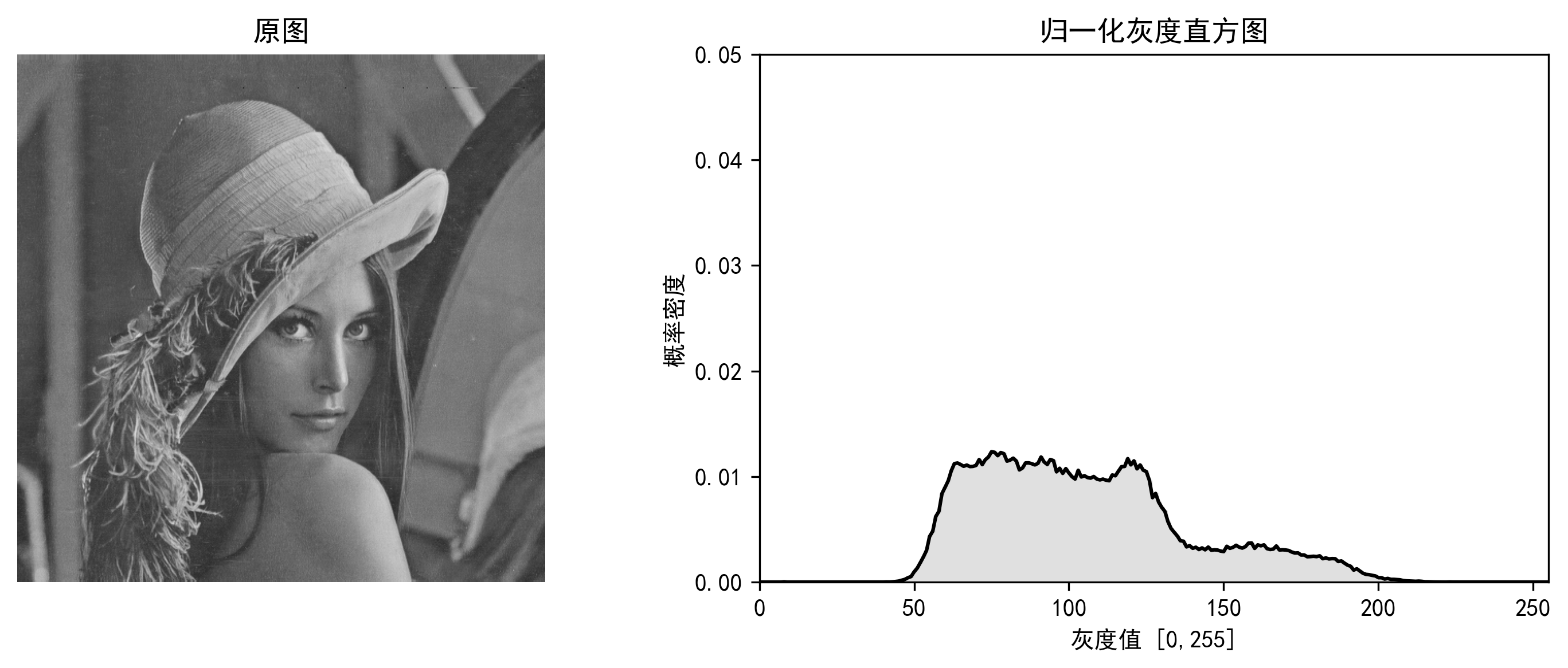
我们可以在直观上描述直方图的意义：

直方图偏左：说明图像大部分像素灰度较低，图像整体偏暗。
直方图偏右：说明图像整体偏亮。
直方图集中在中间：说明图像对比度较低，看起来灰蒙蒙。
直方图分布均匀：图像的亮度和对比度较为均衡。

什么是直方图均衡化

直方图均衡化的目标是让图像的灰度分布变得均匀，即让每个灰度级出现的概率大致相等。这样做的理论基础是，一个具有均匀灰度分布的图像拥有最高的熵，因此可以呈现出最多的信息和最高的对比度。在连续域中，不管原始图像的直方图分布如何，我们总是可以将其变换为均匀分布直方图，如下图：

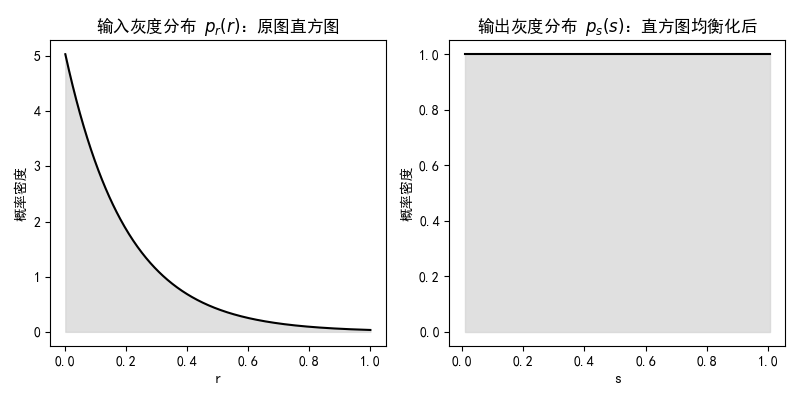
要实现以上目标，我们需要找到一个映射函数（Transform Function） $s=T(r)$ ，将原始灰度 $r$ 映射到新的灰度级 $s$ 。该映射按时需要满足两个条件：

$s=T(r)$ 在 $0\leqslant r \leqslant L-1$ 区间上单调递增，以保持像素亮度的相对顺序（即变换后亮像素始终比暗像素亮）。
$s=T(r)$ 的值域与 $r$ 相同，即 $0\leqslant s\leqslant L-1$ 。

数学上，我们可以利用累积分布函数（Cumulative Distribution Function, CDF） 来构建这个映射函数。

设原始图像的灰度级 $r$ 的概率密度函数(PDF)为 $p_{r}(r)$ ，累积分布函数(CDF)是概率密度函数(PDF)的积分： $C(r)=\int_{0}^{r}p_{r}(\omega )d \omega$ 。

回顾之前定义的映射函数 $s=T(r)$ 所需要满足的两个条件，函数 $C(r)=\int_{0}^{r}p_{r}(\omega )d \omega$ 满足条件1，即满足单调递增。而函数 $C(r)=\int_{0}^{r}p_{r}(\omega )d \omega$ 的值域为 $[0,1]$ ，我们只需要将其乘以 $L-1$ 即可满足值域为 $[0,L-1]$ 。因此，定义 $s=T(r)=(L-1)\int_{0}^{r}p_{r}(\omega)d \omega$ 满足映射函数的所有条件。

接下来，为什么该变换可以使得变换后概率分布 $p_{s}(s)$ 均匀分布呢？我们可以通过随机变量之间的关系予以证明。

已知输入图像的概率密度 $p_{r}(r)$ ，且已知变换函数 $s=T(r)$ ，则待求解的变换后概率密度可表示为： $p_{s}(s)=p_{r}(r)\left | \frac{dr}{ds} \right |$ ，这是概率理论中的一个基本关系。

根据 $s=T(r)$ 可求解 $\frac{ds}{dr}=(L-1)\frac{d}{dr}[\int_{0}^{r}p_{r}(\omega)d \omega]=(L-1)p_{r}(r)$ ，

带入 $p_{s}(s)=p_{r}(r)\left | \frac{dr}{ds} \right |$ 可求解 $p_{s}(s)=p_{r}(r)\frac{1}{(L-1)p_{r}r}=\frac{1}{L-1}$ 。

以上推导表明：变换后的概率密度为一条均匀分布的直线，这就是我们进行直方图均衡化的理论基础。我们期望变换后的图像的灰度级分布尽可能的趋近一条均匀分布的直线，使得图像呈现出更多的信息和更高的对比度。

对于真实图像而言，我们总是需要处理离散情况，我们可以定义离散灰度级 $r _{k}$ 的概率密度函数 $p_{r}(r_{k})=\frac{n_{k}}{N}$ ，其中 $n_{k}$ 为灰度级 $r _{k}$ 的像素数， $N$ 为图像的总像素数。

然后使用累积和替代积分有 $s_{k}=T(r_{k})=(L-1)\sum_{j=0}^{k}\frac{n_{j}}{N}$ ，到此实现了离散情况下的直方图均衡化变换。

直方图均衡化的手动实现

// src,dst: 原图与变换后图像，仅支持单通道图像
// dst_hist: 定义均衡化后直方图区间，默认区间为[0,255]，可通过调整区间进行自定义映射
void HistEqualization(cv::Mat& src, cv::Mat& dst, cv::Point dst_hist = cv::Point(0, 255))
{
	// 仅处理灰度图像
	// 对于彩色图像，可首先将其转换到Lab空间，然后在L通道上进行直方图均衡化，最后再反变换到BGR空间
	if (src.empty() || src.channels() != 1)
		return;

	// 手动计算图像直方图
	unsigned int hist[256];
	memset(hist, 0, 256 * sizeof(unsigned int));
	for (int row = 0; row < src.rows; ++row)
	{
		uchar* datasrc = src.ptr<uchar>(row);
		for(int col = 0; col < src.cols; ++col)
		{ 
			++hist[datasrc[col]];
		}
	}

	// 根据直方图均衡化策略构造查找表
	// 默认情形下，原图被均衡化到[0,255]区间，也可以根据需求修改目标区间
	cv::Mat lut(1, 256, CV_8UC1);
	uchar* lutdata = lut.ptr();
	int cumulative = 0;
	int   histCnt = src.rows * src.cols;
	for (int i = 0; i < 256; ++i)
	{
		cumulative += hist[i];
		lutdata[i] = (uchar)((dst_hist.y - dst_hist.x) * cumulative / histCnt + dst_hist.x);
	}

	// 应用直方图均衡化
	cv::LUT(src, lut, dst);
}

以上代码实现了直方图均衡化的手动构造，直方图均衡化的关键点是建立一个变换的查找表，后续仅需要在查找表上工作即可，而不需要对每个像素进行计算。参数dst_hist定义了变换后直方图区间，默认情况下为 $[0,255]$ ，我们可以根据实际需求进行调整。

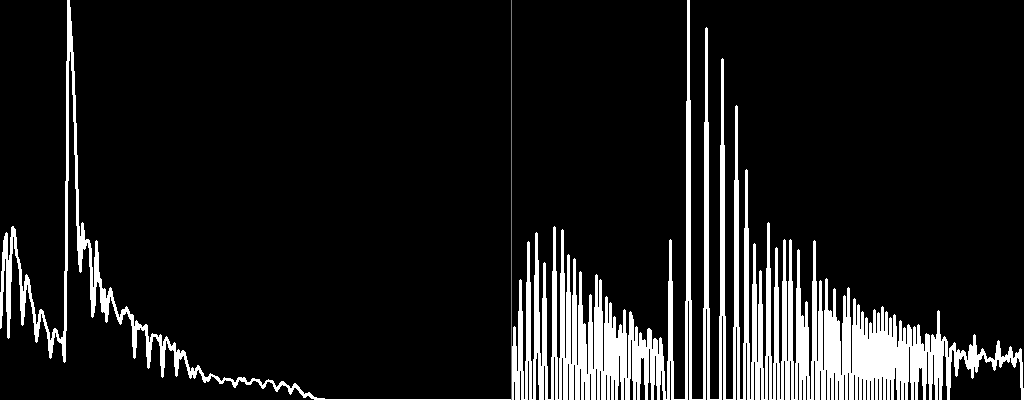
上图展示了一幅夜景图像经过直方图均衡化后的效果。我们可以明显感受到直方图均衡化后图像更加清晰，同时直方图分布也更加"均匀"。

这里我们可能会有一个疑问：为什么变换后直方图没有呈现出一个均匀的分布？这是由于我们处理的是离散数据：如果某个灰度点上的统计数量大于图像总数的 $\frac{1}{256}$ ，则一定会使得变换后直方图在某个点上的有一个较大的峰值。同样的，由于该灰度点占据了大量的统计数，在峰值附近一定会有一些对应的谷值(或空隙)，从而平衡该灰度点产生的影响。

使用OpenCV进行直方图均衡化

OpenCV提供了cv::equalizeHist函数实现直方图均衡化。参数src和dst分别表示输入与输出图像，且要求输入图像为单通道灰度图，因为直方图的相关概念均在单通道图像上定义。如果我们想对彩色图像进行直方图均衡化，一个比较好的策略是首先进行色彩空间变换以提前图像的亮度通道(如BGR2LAB)，然后在亮度通道上进行直方图均衡化，最后再变换到BGR空间中。

以下代码实现了彩色图像的直方图均衡化：

int main() {

	cv::Mat img_src = cv::imread("src4.bmp", cv::IMREAD_COLOR);
	if (img_src.empty())
		return 0;
	
	// 将BGR图像变换到LAB空间
	cv::Mat img_lab;
	cv::cvtColor(img_src, img_lab, cv::COLOR_BGR2Lab);

	std::vector<cv::Mat> lab_planes(3);
	cv::split(img_lab, lab_planes);

	// 对L分量进行直方图均衡化
	cv::equalizeHist(lab_planes[0], lab_planes[0]);

	cv::merge(lab_planes, img_lab);

	// 变换到BGR空间
	cv::Mat img_dst;
	cv::cvtColor(img_lab, img_dst, cv::COLOR_Lab2BGR);

	cv::imwrite("hist_equa.bmp", img_dst);
	
	return 0;
}

如果我们相对某个局部区域进行直方图均衡化，可以使用以下策略：

// 构造一个基于rect_roi的浅拷贝img_roi，img_roi与lab_planes[0]共享数据内存，
// 在equalizeHist传入img_roi即可实现局部ROI的直方图均衡化
cv::Rect rect_roi(50, 50, 300, 300);
cv::Mat img_roi = lab_planes[0](rect_roi);
cv::equalizeHist(img_roi, img_roi);

效果如下：

对比度受限的自适应直方图均衡化

虽然直方图均衡化效果显著，但它有一个明显的缺点：全局性。它对整张图像应用一个统一的变换，这在某些情况下会导致问题。例如，在一张包含大片暗区域和一小块亮区域的图像中，全局均衡化会为了提升暗区域的对比度，而过度拉伸亮区域，导致亮区域出现过度增强和细节丢失。

为了克服全局直方图均衡化的局限性，自适应直方图均衡化（Adaptive Histogram Equalization, AHE） 应运而生。AHE将图像分割成多个小区域（称为“块”或“tiles”），并对每个区域独立进行直方图均衡化。这种局部处理方式可以有效提升局部对比度，避免了全局均衡化的“一刀切”问题。

但AHE也并非完美。它在处理图像边界时可能引入不自然的边界伪影（artifacts），并且在某些均匀区域（如天空）过度增强噪声。对比度受限的自适应直方图均衡化（Contrast Limited Adaptive Histogram Equalization,CALHE）正是为解决这些问题而提出的AHE的改进版本。

CLAHE的核心思想是在局部自适应的基础上，引入对比度限制（Contrast Limiting）。它在对每个区域的直方图进行均衡化之前，对直方图的高度进行限制。基本步骤如下：

分块（Tiling）：将图像划分为多个不重叠小区域。
直方图计算：对每个区域计算其直方图。
对比度限制（Clipping）：这是CLAHE最关键的一步。
a. 首先，设定一个限制阈值（clip limit）。这个阈值通常是该区域直方图平均高度的倍数。
b. 然后，遍历直方图的每个灰度级。如果某个灰度级的像素数超过了这个阈值，就将超出部分的像素数截断（clip）下来。
c. 将所有被截断的像素数平均分配给直方图中的其他灰度级，使直方图的总像素数保持不变。这个过程可以平滑直方图，防止某些灰度级因数量过多而过度拉伸。
直方图均衡化：对每个经过裁剪的直方图进行均衡化。
插值（Interpolation）：为了消除分块处理带来的边界伪影，CLAHE采用双线性插值或更高级的插值方法，将每个像素的新灰度值由其周围四个区域的均衡化结果加权平均得到。这使得过渡更加平滑自然。

对于以上步骤，除了插值，其他基本上都是显而易见的。为了更加深入理解插值，我们假设 $P(x,y)$ 处于如下相邻小块的交界处：

Tile00 | Tile01
-------+-------
Tile10 | Tile11

四个 tile 的映射函数分别为 $f_{00},f_{01},f_{10},f_{11}$
$P(x,y)$ 相对于左上角Tile00的坐标为 $\left\{\begin{matrix} dx=\frac{x-x_{0}}{tile_width}\\ dy=\frac{y-y_{0}}{tile_height} \end{matrix}\right.$
双线性插值输出为： $P_{out}=(1-dx)(1-dy)f_{00}(P)+dx(1-dy)f_{01}(P)+(1-dx)dyf_{10}(P)+dxdyf_{11}(P)$

使用OpenCV进行CLAHE

OpenCV提供了对比度受限的自适应直方图均衡化(CLAHE)的实现，我们首先需要创建一个cv::CLAHE对象，在创建对象时确定局部分块尺寸以及裁剪限定阈值。

cv::Mat img_dst;
cv::Ptr<cv::CLAHE> clahe = cv::createCLAHE(20., cv::Size(16, 16));
clahe->apply(img_src, img_dst);

以上是调用OpenCV的CLAHE的关键代码，函数 cv::createCLAHE(20., cv::Size(16, 16))确定了CLAHE的所有特性。

tileGridSize：图像被划分为16*16的不重叠小块，在每个块中进行直方图均衡化。
clipLimit：对原始直方图对比度限制的阈值。如我们这里使用了16*16的小块，则直方图的每个bin上平均数量为 $\frac{16*16}{256}$ (即为1)，再乘以clipLimit(20)得到对比度限制阈值。
后续算法使用以上公式计算的对比度阈值对直方图进行裁平处理，并将移除像素均匀的分布到所有的bin中。

根据以上描述，clipLimit的大小产生如下效果：

当clipLimit很小(如接近1)，对比度增强效果越弱，但能够很好的抑制噪声。
当clipLimit很大，对比度增强效果明显，同时也带来了更强的噪声放大和伪影。

从左到右：角膜内皮原图，clipLimit=2，clipLimit=5，clipLimit=20

总结

本文讲解了直方图均衡化的相关知识，直方图均衡化作为图像增强的基本方法之一有着广泛的应用。我们首先讲解了直方图与直方图均衡化相关的原理，然后根据理论手动构造了一个直方图均衡化算法，这样有利于我们深入理解直方图均衡化的基本原理。接下来我们讨论了OpenCV提供的相关接口，最后我们介绍了对比度受限的自适应资方图均衡化，该算法可以克服全局直方图均衡化(CLAHE)的一些缺陷。在医学内皮细胞分析中，使用CLAHE算法可以提升细胞对比度，为进一步细胞识别构造了一个有利的基础。