如何绘制CIE1931xy色度图

最新推荐文章于 2025-04-14 12:08:41 发布

luoganttcc

最新推荐文章于 2025-04-14 12:08:41 发布

阅读量5.7k

点赞数 9

分类专栏： isp 文章标签： matlab 开发语言

原文链接：https://blog.csdn.net/weixin_43194305/article/details/115468614?spm=1001.2101.3001.6650.7&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7ERate-7-115468614-blog-88884669.pc_relevant_3mothn_strategy_recovery&depth_1-utm

版权

isp 专栏收录该内容

20 篇文章

订阅专栏

如何绘制CIE1931xy色度图

文章目录

如何绘制CIE1931xy色度图

转载请注明出处

一点点介绍

色度学和CIE1931xyY色空间

既然要绘制这个图，大家应该对xy色品坐标有所了解。

如果不是很了解的可以参考这个CIE1931xyY色度图-复旦大学.ppt了解一下基本的色度学知识。

简单说明一下：

色度图中的外形轮廓线是可见光范围里(约380nm-760nm)单色光颜色轨迹线
等能白点E的坐标xy(0.3333,0.3333)

一点点补充说明

大家在网上应该可以找到五花八门的色度图，让人很难分辨到底哪个才是标准的。

对于部分问题，大家可能会有所疑惑的，在这里简单说明：

真正意义上的色度图在现有的显示设备上根本显示不了，所以相比于纠结图中的颜色是否准确，应该更加关注坐标数据，这才是将颜色量化为xy坐标的意义。不过能画的好看一些确实有助于理解相关概念。
颜色是三维的，色品图是二维的，所以色度图不包含亮度信息。等能白点周围的颜色并不是只有白色，所有灰色、黑色都位于这里。

这里附上几种常见色域在色品图上的位置，图片来源:深入理解 sRGB\Adobe RGB\NTSC\DCI-P3\REC.2020\ProPhoto RGB 色域

gamut

获取途径和绘制方法

这部分主要来介绍一下如何获取这个图以及如何在科研、项目里用这个图。

SVG格式

维基百科上提供的SVG格式的图片，以及不同分辨率的PNG图片，可以自行取用。

https://commons.wikimedia.org/wiki/File:CIE1931xy_blank.svg

在这里插入图片描述

Matlab自带函数

在matlab 2017b及之后的版本中引入了函数plotChromaticity用于绘制色度图。

最简单的用法，直接调用函数，hold on之后自己就可以在上面涂涂画画了。

plotChromaticity
hold on
## your code ...

  
  
  
  1
2
3

绘制结果如下图所示:

在这里插入图片描述

简单说下matlab的实现思路

matlab绘制色度图的方法是将上面的区域分割成一个个小四边形，从4个顶点的xy值计算颜色，并对内部进行插值填充。matlab使用patch函数绘制填充颜色，

patch('Vertices',v, 'Faces',f, 'EdgeColor','none', 'FaceVertexCData',xy4rgb(i:i+3,3:5),'FaceColor','interp');

  
  
  
  1

我们将其中控制线条的'EdgeColor','none'参数改为'EdgeColor','k'可以得到以下结果，方便大家更加形象的了解渐变填充过程。

在这里插入图片描述

因为其实每个点只能得到xyz坐标（

    z
   
   
    =
   
   
    1
   
   
    −
   
   
    x
   
   
    −
   
   
    y
   
  
  
   z=1-x-y
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.43056em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.04398em;">z</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 0.72777em; vertical-align: -0.08333em;"></span><span class="mord">1</span><span class="mspace" style="margin-right: 0.222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.222222em;"></span></span><span class="base"><span class="strut" style="height: 0.66666em; vertical-align: -0.08333em;"></span><span class="mord mathdefault">x</span><span class="mspace" style="margin-right: 0.222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.222222em;"></span></span><span class="base"><span class="strut" style="height: 0.625em; vertical-align: -0.19444em;"></span><span class="mord mathdefault" style="margin-right: 0.03588em;">y</span></span></span></span></span>），是计算不了对应的RGB颜色的，还缺少一个<strong>Y</strong>来控制亮度信息。matlab里实现时候调用了以下代码来将xyz值转为srgb数值：</p>

rgb = images.internal.testchart.xyz2srgb(xyz');

 
 
 
 1

所以可以看到，matlab版本的绘制结果在等能白点周围都是以灰色填充，这取决里matlab具体的换算实现。这个说明顺便帮忙解答我师弟博客下的提问：为什么matlab绘制的色度图白点周围不是白色填充？当然了，我在前面就说了，所有无彩色都集中在这个区域。

另外，这个函数还有几个带参数的重载版本，可以用于绘制一些额外的数据上去，有兴趣的朋友可以参考官方文档中的example学习。

顺便一提，在matlab里进入该函数，里面包含了单色光轨迹线上的63对xy坐标值可用。

更加详细的光谱色度坐标可以参考1931CIE-XYZ标准色度系统。

Qt下用C++绘制的两种思路

由于可能需要在项目里用到，就需要自己实现一下啦，这里给出了在两种在Qt框架下的绘制方法。

借助了Qt的线性渐变类QLinearGradient来进行颜色填充。

QGradient Class是Qt的渐变填充类，结合QBrush可对任意区域实现快速渐变填充。目前Qt支持三种渐变模式，这里采用线性渐变进行填充。

受matlab填充方式启发，这里选择从等能白点处，即xy(0.3333,0.3333)向单色光轮廓线进行三角区域填充。

QLinearGradient需要设置填充起点坐标和填充终点坐标，填充起点颜色和填充终点颜色，现有数据为：

填充起点坐标：白点（已知）
填充终点坐标：曲线轮廓点（已知，需要插值扩充，下方的直线在已知端点的情况下可自行选择填充点的数量）
填充起点颜色：可以人为设定白色或者偏灰色，仅为了方便显示和理解（已知）
填充终点颜色：人为选取单色光谱中近似对应的蓝色、青色、绿色、黄色、红色五个点，其余点通过插值计算。（已知+计算）

填充颜色的计算方法，即最简单的线性插值计算。但实际上轮廓线是曲线，线性插值会存在一点误差。颜色插值混合可以近似采用格拉斯曼颜色混合定律，假设曲线上蓝色

    B
   
  
  
   B
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.05017em;">B</span></span></span></span></span>和青色<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    C
   
  
  
   C
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.07153em;">C</span></span></span></span></span>之间任意一点，与蓝色距离<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     d
    
    
     1
    
   
  
  
   d_1
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.84444em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathdefault">d</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>，与青色距离<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     d
    
    
     2
    
   
  
  
   d_2
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.84444em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathdefault">d</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>，相对位置<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    p
   
   
    =
   
   
    
     
      d
     
     
      1
     
    
    
     
      
       d
      
      
       1
      
     
     
      +
     
     
      
       d
      
      
       2
      
     
    
   
  
  
   p=\frac{d_1}{d_1+d_2}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.625em; vertical-align: -0.19444em;"></span><span class="mord mathdefault">p</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 1.34131em; vertical-align: -0.4451em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.896208em;"><span class="" style="top: -2.655em;"><span class="pstrut" style="height: 3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight"><span class="mord mathdefault mtight">d</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.317314em;"><span class="" style="top: -2.357em; margin-left: 0em; margin-right: 0.0714286em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.143em;"><span class=""></span></span></span></span></span></span><span class="mbin mtight">+</span><span class="mord mtight"><span class="mord mathdefault mtight">d</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.317314em;"><span class="" style="top: -2.357em; margin-left: 0em; margin-right: 0.0714286em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.143em;"><span class=""></span></span></span></span></span></span></span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.4101em;"><span class="pstrut" style="height: 3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight"><span class="mord mathdefault mtight">d</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.317314em;"><span class="" style="top: -2.357em; margin-left: 0em; margin-right: 0.0714286em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.143em;"><span class=""></span></span></span></span></span></span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.4451em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span></span></span></span></span>。那么该点的颜色为:</p>

      X
     
     
      
       r
      
      
       ,
      
      
       g
      
      
       ,
      
      
       b
      
     
    
    
     =
    
    
     (
    
    
     1
    
    
     −
    
    
     p
    
    
     )
    
    
     ∗
    
    
     
      B
     
     
      
       r
      
      
       ,
      
      
       g
      
      
       ,
      
      
       b
      
     
    
    
     +
    
    
     p
    
    
     ∗
    
    
     
      C
     
     
      
       r
      
      
       ,
      
      
       g
      
      
       ,
      
      
       b
      
     
    
   
   
    X_{r,g,b}=(1-p)*B_{r,g,b}+p*C_{r,g,b}
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.969438em; vertical-align: -0.286108em;"></span><span class="mord"><span class="mord mathdefault" style="margin-right: 0.07847em;">X</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.336108em;"><span class="" style="top: -2.55em; margin-left: -0.07847em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight" style="margin-right: 0.02778em;">r</span><span class="mpunct mtight">,</span><span class="mord mathdefault mtight" style="margin-right: 0.03588em;">g</span><span class="mpunct mtight">,</span><span class="mord mathdefault mtight">b</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord">1</span><span class="mspace" style="margin-right: 0.222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.222222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathdefault">p</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.222222em;"></span><span class="mbin">∗</span><span class="mspace" style="margin-right: 0.222222em;"></span></span><span class="base"><span class="strut" style="height: 0.969438em; vertical-align: -0.286108em;"></span><span class="mord"><span class="mord mathdefault" style="margin-right: 0.05017em;">B</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.336108em;"><span class="" style="top: -2.55em; margin-left: -0.05017em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight" style="margin-right: 0.02778em;">r</span><span class="mpunct mtight">,</span><span class="mord mathdefault mtight" style="margin-right: 0.03588em;">g</span><span class="mpunct mtight">,</span><span class="mord mathdefault mtight">b</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.222222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.222222em;"></span></span><span class="base"><span class="strut" style="height: 0.65972em; vertical-align: -0.19444em;"></span><span class="mord mathdefault">p</span><span class="mspace" style="margin-right: 0.222222em;"></span><span class="mbin">∗</span><span class="mspace" style="margin-right: 0.222222em;"></span></span><span class="base"><span class="strut" style="height: 0.969438em; vertical-align: -0.286108em;"></span><span class="mord"><span class="mord mathdefault" style="margin-right: 0.07153em;">C</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.336108em;"><span class="" style="top: -2.55em; margin-left: -0.07153em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight" style="margin-right: 0.02778em;">r</span><span class="mpunct mtight">,</span><span class="mord mathdefault mtight" style="margin-right: 0.03588em;">g</span><span class="mpunct mtight">,</span><span class="mord mathdefault mtight">b</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span></span></span></span></span></span></p>

有了上述计算数据，就可以开始绘图了，先把原始数据的63个点进行颜色插值，然后显示出来的效果如下：

在这里插入图片描述

这里说明一下为什么要在这些数据点之间进一步插值，因为当前颜色点的渐变幅度较大，直接计算会造成渐变不连续以及严重的边缘锯齿。

在这里插入图片描述

假设对已有的63对坐标中间，任意两个点之间再插值9个点，并计算对应的颜色，最后得到的单色光离散点轨迹线如下图所示。

在这里插入图片描述

同样基于这些点填充整个色度图，效果如下：

在这里插入图片描述

从效果上看基本可以达到要求，上述填充过程重载了paintEvent函数直接在背景上画，绘制代码如下：

void MainWindow::paintEvent(QPaintEvent*){
    QPainter p(this);
    p.fillRect(rect(),Qt::white);
    p.setRenderHint(QPainter::Antialiasing);
	//坐标缩放
    p.scale(width(), height());
    p.setPen(QPen(QColor(0,0,0,0),1));
QLinearGradient linearGradient<span class="token punctuation">;</span>
<span class="token comment">//等能白点</span>
CPointF <span class="token function">whiteP</span><span class="token punctuation">(</span><span class="token number">1.0</span><span class="token operator">/</span><span class="token number">3</span><span class="token punctuation">,</span> <span class="token number">1.0</span><span class="token operator">/</span><span class="token number">3</span><span class="token punctuation">,</span> <span class="token function">QColor</span><span class="token punctuation">(</span><span class="token number">235</span><span class="token punctuation">,</span><span class="token number">235</span><span class="token punctuation">,</span><span class="token number">235</span><span class="token punctuation">)</span><span class="token punctuation">)</span><span class="token punctuation">;</span>
<span class="token comment">//ciePoints包含边界点和对应颜色</span>
<span class="token keyword">for</span><span class="token punctuation">(</span><span class="token keyword">int</span> i<span class="token operator">=</span><span class="token number">0</span><span class="token punctuation">;</span>i<span class="token operator">&lt;</span>m_time<span class="token operator">-</span><span class="token number">1</span><span class="token punctuation">;</span>i<span class="token operator">++</span><span class="token punctuation">)</span><span class="token punctuation">{<!-- --></span>
    <span class="token comment">//确定三角形绘制域点</span>
    QPointF ps<span class="token punctuation">[</span><span class="token punctuation">]</span><span class="token punctuation">{<!-- --></span>whiteP<span class="token punctuation">.</span><span class="token function">toQPointF</span><span class="token punctuation">(</span><span class="token punctuation">)</span><span class="token punctuation">,</span> ciePoints<span class="token punctuation">[</span>i<span class="token punctuation">]</span><span class="token punctuation">.</span><span class="token function">toQPointF</span><span class="token punctuation">(</span><span class="token punctuation">)</span><span class="token punctuation">,</span> <span class="token number">2</span><span class="token operator">*</span>ciePoints<span class="token punctuation">[</span>i<span class="token operator">+</span><span class="token number">1</span><span class="token punctuation">]</span><span class="token punctuation">.</span><span class="token function">toQPointF</span><span class="token punctuation">(</span><span class="token punctuation">)</span><span class="token operator">-</span>ciePoints<span class="token punctuation">[</span>i<span class="token punctuation">]</span><span class="token punctuation">.</span><span class="token function">toQPointF</span><span class="token punctuation">(</span><span class="token punctuation">)</span><span class="token punctuation">}</span><span class="token punctuation">;</span>
    <span class="token comment">//设置起始坐标，结束坐标，起始颜色，结束颜色</span>
    linearGradient<span class="token punctuation">.</span><span class="token function">setStart</span><span class="token punctuation">(</span>whiteP<span class="token punctuation">.</span><span class="token function">toQPointF</span><span class="token punctuation">(</span><span class="token punctuation">)</span><span class="token punctuation">)</span><span class="token punctuation">;</span>
    linearGradient<span class="token punctuation">.</span><span class="token function">setFinalStop</span><span class="token punctuation">(</span>ciePoints<span class="token punctuation">[</span>i<span class="token punctuation">]</span><span class="token punctuation">.</span><span class="token function">toQPointF</span><span class="token punctuation">(</span><span class="token punctuation">)</span><span class="token punctuation">)</span><span class="token punctuation">;</span>
    linearGradient<span class="token punctuation">.</span><span class="token function">setColorAt</span><span class="token punctuation">(</span><span class="token number">0.0</span><span class="token punctuation">,</span> whiteP<span class="token punctuation">.</span><span class="token function">C</span><span class="token punctuation">(</span><span class="token punctuation">)</span><span class="token punctuation">)</span><span class="token punctuation">;</span>
    linearGradient<span class="token punctuation">.</span><span class="token function">setColorAt</span><span class="token punctuation">(</span><span class="token number">1.0</span><span class="token punctuation">,</span> ciePoints<span class="token punctuation">[</span>i<span class="token punctuation">]</span><span class="token punctuation">.</span><span class="token function">C</span><span class="token punctuation">(</span><span class="token punctuation">)</span><span class="token punctuation">)</span><span class="token punctuation">;</span>
    
    p<span class="token punctuation">.</span><span class="token function">setBrush</span><span class="token punctuation">(</span><span class="token punctuation">(</span><span class="token function">QBrush</span><span class="token punctuation">(</span>linearGradient<span class="token punctuation">)</span><span class="token punctuation">)</span><span class="token punctuation">)</span><span class="token punctuation">;</span>
    p<span class="token punctuation">.</span><span class="token function">drawPolygon</span><span class="token punctuation">(</span>ps<span class="token punctuation">,</span> <span class="token number">3</span><span class="token punctuation">)</span><span class="token punctuation">;</span>
<span class="token punctuation">}</span>

}

最后再加一个坐标轴以及自适应拉伸就可以使用了，这里其实可以明显看到蓝色和红色处在曲线轮廓线和直线交界处的过渡有点问题，需要特殊处理，再扫描一下覆盖这条白线。不过说到底还是绘制方式的问题，所以这里还是推荐用第二种绘制方法。

在这里插入图片描述

自己计算每个像素位置的填充颜色，方便在各类语言和框架下实现。

绘图函数的主要流程都在下面的代码中了，也标注了每一步的功能，整体思路上应该比较容易理解。

QImage CIEDiagram::drawCIEDiagram(int picSize){
	//创建QImage对象
    QImage cieDiagram(picSize, picSize, QImage::Format_RGB32);
    cieDiagram.fill(Qt::white);
<span class="token comment">//遍历像素</span>
<span class="token keyword">for</span><span class="token punctuation">(</span><span class="token keyword">int</span> y<span class="token operator">=</span><span class="token number">0</span><span class="token punctuation">;</span>y<span class="token operator">&lt;</span>picSize<span class="token punctuation">;</span>y<span class="token operator">++</span><span class="token punctuation">)</span><span class="token punctuation">{<!-- --></span>
    QRgb<span class="token operator">*</span> line <span class="token operator">=</span> <span class="token punctuation">(</span>QRgb <span class="token operator">*</span><span class="token punctuation">)</span>cieDiagram<span class="token punctuation">.</span><span class="token function">scanLine</span><span class="token punctuation">(</span>y<span class="token punctuation">)</span><span class="token punctuation">;</span>
    <span class="token keyword">for</span><span class="token punctuation">(</span><span class="token keyword">int</span> x<span class="token operator">=</span><span class="token number">0</span><span class="token punctuation">;</span>x<span class="token operator">&lt;</span>picSize<span class="token punctuation">;</span>x<span class="token operator">++</span><span class="token punctuation">)</span><span class="token punctuation">{<!-- --></span>
        CPointF <span class="token function">curP</span><span class="token punctuation">(</span><span class="token number">1.0</span><span class="token operator">*</span>x<span class="token operator">/</span>picSize<span class="token punctuation">,</span><span class="token number">1.0</span><span class="token operator">-</span><span class="token number">1.0</span><span class="token operator">*</span>y<span class="token operator">/</span>picSize<span class="token punctuation">)</span><span class="token punctuation">;</span><span class="token comment">//将像素位置转换为xy逻辑坐标</span>
        <span class="token keyword">if</span><span class="token punctuation">(</span><span class="token function">isPointInsideBound</span><span class="token punctuation">(</span>curP<span class="token punctuation">)</span><span class="token punctuation">)</span><span class="token punctuation">{<!-- --></span><span class="token comment">//判断当前像素点是否在CIE色度曲线内</span>
            CLineF <span class="token function">whiteP</span><span class="token punctuation">(</span>white<span class="token punctuation">,</span> curP<span class="token punctuation">)</span><span class="token punctuation">;</span><span class="token comment">//构造一个白点与当前像素点的射线</span>
            CPointF crossPoint<span class="token punctuation">;</span>
            areaFlag areaflag <span class="token operator">=</span> <span class="token function">crossArea</span><span class="token punctuation">(</span>curP<span class="token punctuation">)</span><span class="token punctuation">;</span><span class="token comment">//判断射线交曲线于哪个区域</span>
            <span class="token comment">//根据相交区域计算射线与CIE轮廓曲线交点</span>
            <span class="token keyword">switch</span> <span class="token punctuation">(</span>areaflag<span class="token punctuation">)</span> <span class="token punctuation">{<!-- --></span>
            <span class="token keyword">case</span> leftA<span class="token operator">:</span>
                crossPoint <span class="token operator">=</span> <span class="token function">getCrossPoint</span><span class="token punctuation">(</span>whiteP<span class="token punctuation">,</span> colorPointIdx<span class="token punctuation">[</span>bottom<span class="token punctuation">]</span><span class="token punctuation">,</span> colorPointIdx<span class="token punctuation">[</span>top<span class="token punctuation">]</span><span class="token punctuation">)</span><span class="token punctuation">;</span>
                <span class="token keyword">break</span><span class="token punctuation">;</span>
            <span class="token keyword">case</span> rightA<span class="token operator">:</span>
                crossPoint <span class="token operator">=</span> <span class="token function">getCrossPoint</span><span class="token punctuation">(</span>whiteP<span class="token punctuation">,</span> colorPointIdx<span class="token punctuation">[</span>top<span class="token punctuation">]</span><span class="token punctuation">,</span> colorPointIdx<span class="token punctuation">[</span>right<span class="token punctuation">]</span><span class="token punctuation">)</span><span class="token punctuation">;</span>
                <span class="token keyword">break</span><span class="token punctuation">;</span>
            <span class="token keyword">default</span><span class="token operator">:</span>
                crossPoint <span class="token operator">=</span> <span class="token function">getCrossPoint</span><span class="token punctuation">(</span>whiteP<span class="token punctuation">,</span> colorPointIdx<span class="token punctuation">[</span>right<span class="token punctuation">]</span><span class="token punctuation">,</span> cieCurvePoints<span class="token punctuation">.</span><span class="token function">size</span><span class="token punctuation">(</span><span class="token punctuation">)</span><span class="token punctuation">)</span><span class="token punctuation">;</span>
                <span class="token keyword">break</span><span class="token punctuation">;</span>
            <span class="token punctuation">}</span>
            CLineF <span class="token function">whiteToBoundLine</span><span class="token punctuation">(</span>white<span class="token punctuation">,</span> crossPoint<span class="token punctuation">)</span><span class="token punctuation">;</span><span class="token comment">//构建白点与交点线段</span>
            QColor c <span class="token operator">=</span> whiteToBoundLine<span class="token punctuation">.</span><span class="token function">getInterColor</span><span class="token punctuation">(</span>curP<span class="token punctuation">)</span><span class="token punctuation">;</span><span class="token comment">//根据白点、当前像素点、交点进行插值，计算当前像素点颜色</span>
            line<span class="token punctuation">[</span>x<span class="token punctuation">]</span> <span class="token operator">=</span> c<span class="token punctuation">.</span><span class="token function">rgb</span><span class="token punctuation">(</span><span class="token punctuation">)</span><span class="token punctuation">;</span>
        <span class="token punctuation">}</span>
    <span class="token punctuation">}</span>
<span class="token punctuation">}</span>

<span class="token keyword">return</span> cieDiagram<span class="token punctuation">;</span>

}

最后效果如下：
在这里插入图片描述

Qt的源码写的比较乱，最近比较忙，之后整理好了发出来，或者急需的，可以留邮箱

一点点小结

在很多颜色处理的地方都用到了近似颜色插值，从人眼效果上来看基本上是符合的。这主要还是因为实际上人眼能够感知并且分辨的颜色不过几千种，当颜色比较多的时候，这种微小变化对人眼就不会很敏感了，即使我们插值的结果不是很准。

所以在实际使用中，完全可以事先准备一副分辨率较高的色度图，然后要缩放的时候直接对图像线性插值即可，颜色效果完全可以满足需求。只需要把边界轮廓实时绘制一下消除锯齿即可。不过如果用的是矢量图那就完全OK啦。

工作比较忙，鸽了好久，更新一下，2022/01/21。

修改了之前的部分代码，封装了一个纯C++导出图像buffer的库
增加一个简易的CIE XY Chromatictiy PlotDemo
增加了基于OpenGL实现的Demo

代码自取，在Github上。

简易的plot demo，应该用Qt画个边框，不然锯齿有点明显。。
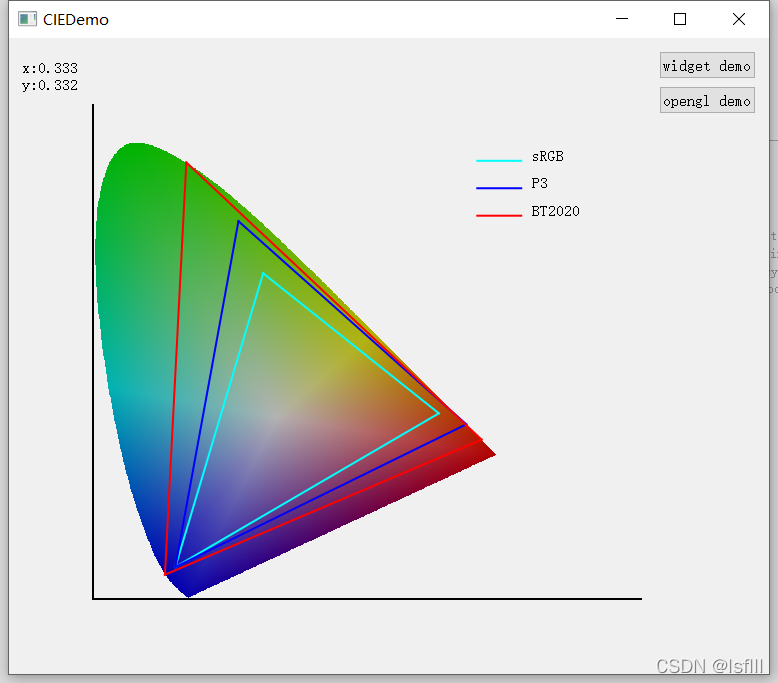
在这里插入图片描述
这是基于qt封装的opengl绘制的，opengl的部分的代码基本是照着网上的教程来的。
opengl的片段着色器能够自动插值，绘图逻辑突然简单了，只要给出外围的光谱轨迹的顶点坐标和颜色就行。

Python上用这个库

有个colour-science的库，基本整合了颜色科学里的大部分工具，可以说是科研工作的好帮手，直接

pip install colour-science

import colour
import colour.plotting # 绘图的好像是导入这个

具体的介绍我之后抽时间再写写，这个文档挺详细的，大家搜一下应该就可以搜到

[link](https://blog.csdn.net/weixin_43194305/article/details/115468614?spm=1001.2101.3001.6650.7&utm_medium=distribute.pc_relevant.none-task-blog-2~default~BlogCommendFromBaidu~Rate-7-115468614-blog-88884669.pc_relevant_3mothn_strategy_recovery&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2~default~BlogCommendFromBaidu~Rate-7-115468614-blog-88884669.pc_relevant_3mothn_strategy_recovery&utm_relevant_index=12)