算法导论--动态规划（0-1背包问题）

背包问题

小偷发现了n个商品，第i个商品重量为$w_i$,价值为$v_i$。小偷希望尽量拿走价值高的商品，但是他的背包只能容纳W重的商品。求如何取舍这些商品？
由于对一个商品，要么被拿走要么不被拿走，所以被称为0-1背包问题。
我们如果采取枚举法进行比较，将会有$2^n$个情况，算法复杂度与n呈指数关系。
下面分析背包问题的性质：

动态规划

最优子结构

令$x_i$=1,表示第i个商品被拿走，$x_i$=0,表示第i个商品不被拿走。
则问题变为求$V=max\sum _{i=1}^nx_iv_i$约束条件为$\sum _{i=1}^nx_iw_i \leq W$,求最大值的$x_1,x_2,x_3..x_n$解；
对于第k个商品，决定是否装包，需要进行比较，如果拿装包即$x_k = 1$,求子问题$V'=max\sum _{i=1}^nx_iv_i(i\neq k)$,约束条件为$\sum _{i=1}^nx_iw_i (x\neq k)\leq W-w_k$。如果不装包，$x_k = 0$，$V''=max\sum _{i=1}^nx_iv_i(i\neq k)$,约束条件不变$\sum _{i=1}^nx_iw_i (x\neq k)\leq W$ 。比较$V'与V''$大小。

自底向上求解方案

算法复杂度为O(nW)
令c[i][j]表示第1个商品到第i个商品中，背包容量为j的情况下，可获得的最大价值；

决定是否选择商品i的方案，比较选与不选的获得的价值
c[i][j] = max(c[i-1][j] ,v[i]+c[i-1][j-w[i]])
例：

int w[]={0,3,6,3,8,6};//商品重量 第一数值为0，为了方便编程
int v[]={0,4,6,6,12,10};//商品价值 第一数值为0，为了方便编程
int W = 10; //背包容量
int c[6][11]={0};//c[i][j]表示在商品1到i中，背包容量为j时，最大价值

采用自底向上求解方案，先填写第一行c[1][j]，此时只有商品1可选，当$j<w[1]$时，背包容量小于商品1的大小，所以c[1][j] =0,当$j\geq w[1]$时，背包内价值即为商品1的价值c[1][j] = v[1]=4;

填写第二行：c[2][j],此时可选商品为1和2 。当$j<w[2]$,商品2一定装不了，但可能装下商品1，所以即c[2][j] = c[1][j],当$j\geq w[2]$,此时可以装下商品2，如当j=6时，如果选择商品2，那么此时背包容量为j-w[2]=0，留给商品1用，而c[1][0]=0,所以背包价值为c[2][6]=v[2]+c[1][0];如果不选商品2，则c[2][6]=c[1][6]=4,比较大小得到，应该把商品2装包。即c[2][6]=v[2]+c[1][0]=6+0=6；
又如:当j=10时，如果选择商品2，则背包容量还剩j-w[2]=4;而c[1][4]=4,此时背包总价值为c[2][10]=v[2]+c[1][4]=6+4=10;如果不选商品2，c[2][10] =c[1][10]=4;选取最大值即c[2][10]=10；

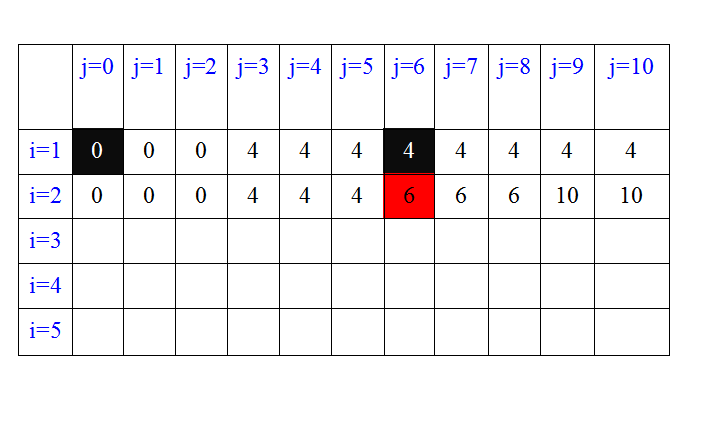
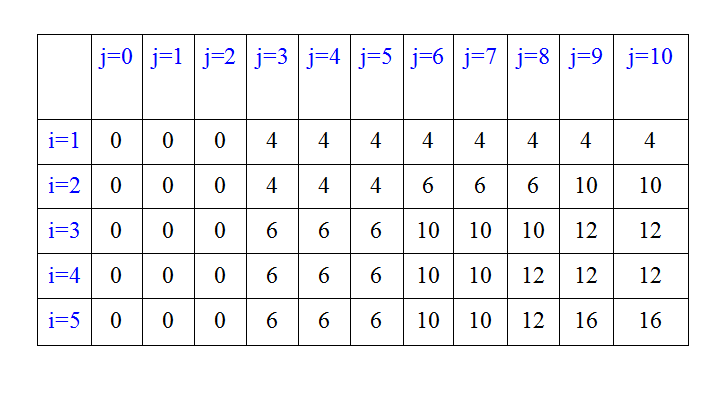
按照上述方式自底向上填写表格：

构造最优解

按照上面描述：如果c[i][j] = c[i-1][j],表明商品i没有被选择；否则就被选择
从表格的右下端开始，即c[5][10]，回溯。
如$c[5][10] \neq c[4][10]$则商品5被选择，而此时背包容量j-w[5]=4;继续向上回溯，比较c[4][4]=c[3][4],表明商品4不选。回溯到第一个商品时，如果$c[1][j]\neq 0$,表明被装包；

完整代码

/************************************************************************
CSDN 勿在浮沙筑高台 
http://blog.csdn.net/luoshixian099
算法导论--动态规划（0-1背包问题）
2015年6月19日                    
************************************************************************/
#include <iostream>
using namespace std;
#define max(a,b) (((a) > (b)) ? (a) : (b))
int w[]={0,3,6,3,8,6};//商品重量
int v[]={0,4,6,6,12,10};//商品价值
int W = 10; //背包容量
int c[6][11]={0};//c[i][j]表示在商品1到i中，背包容量为j时，最大价值
void Package0_1(int w[],int v[],int W,int n,int c[][11])//
{

    for(int i=1;i<=n;i++)          //逐行填表c[i][j]
    {
        for (int j=1;j<=W;j++)
        {
            if ( i == 1)       //填写第1行时，不参考其他行
            {
                if (j < w[i])
                    c[i][j]=0;
                else
                    c[i][j] = v[i];
            }

            else
            {
                if ( j < w[i])  //背包容量小于商品i的重量，商品i一定不选
                {
                    c[i][j] = c[i-1][j];
                }
                else
                {
                    c[i][j] = max(c[i-1][j],v[i]+c[i-1][j-w[i]]);//比较选与不选商品i的背包总价值大小
                }
            }
        }
    }

    for(int m =1;m<6;m++)
    {
        for (int n=0;n<11;n++)
        {
            cout<<c[m][n]<<"  ";
        }
        cout<<endl;
    }

}
void Print_Package0_1(int c[][11])  //构造解
{
    int i=5;
    int j=10;
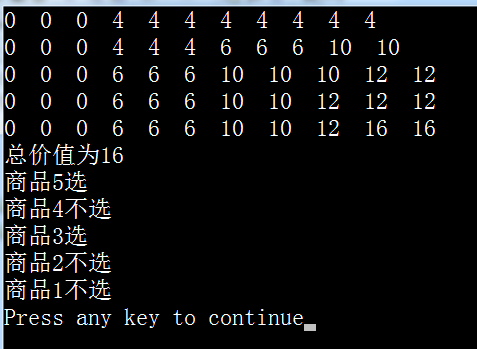
    cout<<"总价值为"<<c[i][j]<<endl;
    while(i!=1)
    {
        if ( c[i][j] == c[i-1][j] )
        {
            cout<<"商品"<<i<<"不选"<<endl;
        }
        else
        {
            cout<<"商品"<<i<<"选"<<endl;
            j = j - w[i];
        }
        i--;
    }

    if ( c[i][j] == 0)   //
    {
        cout<<"商品"<<i<<"不选"<<endl;
    }
    else
    {
        cout<<"商品"<<i<<"选"<<endl;
    }

}
int main()
{

   Package0_1(w,v,W,5,c);
   Print_Package0_1(c);
   return 0;
}