第五章:数学运算
经典案例,并行地求 sin 值
终于可以在GPU上干点正事了 (bushi
就让我们在 GPU 上并行地计算从 sin(0) 到 sin(65535) 的值,并填入到数组 arr 中。
#include <cuda_runtime.h>
#include <cstdio>
#include <vector>
#include "CudaAllocator.h" // 封装刚才的内存分配器
#include "helper_cuda.h"
template <class Func>
__global__ void parallel_for(int n, Func func) {
for (int i = blockDim.x * blockIdx.x + threadIdx.x; i < n;
i += blockDim.x * gridDim.x) {
func(i);
}
}
int main() {
int n = 65536;
std::vector<float, CudaAllocator<float>> arr(n);
parallel_for<<<32, 128>>>(
n, [arr = arr.data()] __device__(int i) { arr[i] = sinf(i); });
checkCudaErrors(cudaDeviceSynchronize());
for (int i = 0; i < n; i++) {
printf("diff %d = %f\n", i, arr[i] - sinf(i));
}
return 0;
}
-
这里为什么用 sinf 而不是 sin?
-
因为 sin 是 double 类型的正弦函数,而我们需要的 sinf 是 float 类型的正弦函数。
-
可不要偷懒少打一个 f 哦,否则计算过程需要对数据类型进行转换,影响性能。
完成同步之后,和 CPU 算出来的比较差值,看看 GPU 算的是否准确无误,从右边的输出可以看到基本是一致的。
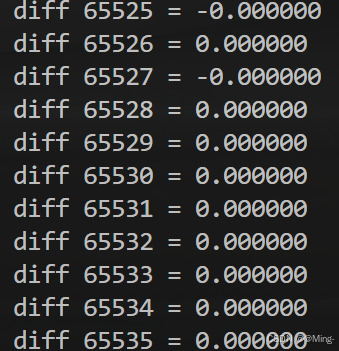
测试一下时间
提供一个小工具:ticktock.h
可以用来打印 CPU 和 GPU的用时
#pragma once
#include <chrono>
#include <iostream>
#ifndef __ycm__
#define TICK(x) auto bench_##x = std::chrono::steady_clock::now();
#define TOCK(x) \
printf("%s: %lfs\n", #x, \
std::chrono::duration_cast<std::chrono::duration<double>>( \
std::chrono::steady_clock::now() - bench_##x) \
.count());
#else
#define TICK(x)
#define TOCK(x)
#endif
注意,这里一定要把 TOCK 放到同步之后。原因之前说过,因为对 GPU 核函数的调用是异步的,只有 cudaDeviceSynchronize() 以后才真正完成执行,才能算出真的时间。
#include <cuda_runtime.h>
#include <cstdio>
#include <vector>
#include "CudaAllocator.h"
#include "helper_cuda.h"
#include "ticktock.h"
template <class Func>
__global__ void parallel_for(int n, Func func) {
for (int i = blockDim.x * blockIdx.x + threadIdx.x; i < n;
i += blockDim.x * gridDim.x) {
func(i);
}
}
int main() {
int n = 1 << 25;
std::vector<float, CudaAllocator<float>> gpu(n);
std::vector<float> cpu(n);
TICK(cpu_sinf); // cpu开始时间
for (int i = 0; i < n; i++) {
cpu[i] = sinf(i);
}
TOCK(cpu_sinf); // cpu结束时间
TICK(gpu_sinf); // gpu开始时间
parallel_for<<<n / 512, 128>>>(
n, [gpu = gpu.data()] __device__(int i) { gpu[i] = sinf(i); });
checkCudaErrors(cudaDeviceSynchronize());
TOCK(gpu_sinf); // gpu结束时间 注意放在GPU同步之后
// for (int i = 0; i < n; i++) {
// printf("diff %d = %f\n", i, gpu[i] - cpu[i]);
//}
return 0;
}
// cpu_sinf: 0.119689s
// gpu_sinf : 0.034462s
查看结果,发现 GPU 比 CPU 快了很多,这是当然的。
- 有时候可能出现GPU比CPU慢很多,或者两次运行GPU速度差距很大
- 这是因为GPU初始化需要准备一些资源,第二次启动时就不需要了
- 所以有时会看到,大佬会先空调用一下GPU,之后再执行任务。
适当调整板块数量 gridDim 和每板块的线程数量 blockDim,还可以更快一些。可以自己调调看,这里我们就不浪费篇幅了。
顺便一提,这样的数学函数还有 :
| 函数 | 简要功能 |
|---|---|
sqrtf(x) | 返回 x 的平方根。 |
rsqrtf(x) | 返回 x 的倒数平方根,即 1/sqrtf(x)。 |
cbrtf(x) | 返回 x 的立方根。 |
rcbrtf(x) | 返回 x 的倒数立方根,即 1/cbrtf(x)。 |
powf(x, y) | 返回 x 的 y 次幂(x^y)。 |
sinf(x) | 返回 x 的正弦值,x 为弧度制。 |
cosf(x) | 返回 x 的余弦值,x 为弧度制。 |
sinpif(x) | 返回 x * pi 的正弦值,x 为倍数。 |
cospif(x) | 返回 x * pi 的余弦值,x 为倍数。 |
sincosf(x) | 返回一个结构体,包含 x 的正弦值和余弦值,x 为弧度制。 |
sincospif(x) | 返回一个结构体,包含 x * pi 的正弦值和余弦值,x 为倍数。 |
logf(x) | 返回 x 的自然对数(以 e 为底)。 |
log2f(x) | 返回 x 的以 2 为底的对数。 |
log10f(x) | 返回 x 的以 10 为底的对数。 |
expf(x) | 返回 e^x,即 e 的 x 次幂。 |
exp2f(x) | 返回 2^x,即 2 的 x 次幂。 |
exp10f(x) | 返回 10^x,即 10 的 x 次幂。 |
tanf(x) | 返回 x 的正切值,x 为弧度制。 |
atanf(x) | 返回 x 的反正切值(arctan(x)),返回结果是弧度制。 |
asinf(x) | 返回 x 的反正弦值(arcsin(x)),返回结果是弧度制。 |
acosf(x) | 返回 x 的反余弦值(arccos(x)),返回结果是弧度制。 |
fmodf(x, y) | 返回 x 除以 y 后的余数。 |
fabsf(x) | 返回 x 的绝对值。 |
fminf(x, y) | 返回 x 和 y 中的较小值。 |
fmaxf(x, y) | 返回 x 和 y 中的较大值。 |
功能总结:
- 平方根与幂:
sqrtf、rsqrtf、cbrtf、rcbrtf、powf等用于计算数值的平方根、倒数平方根、立方根、倒数立方根和幂。 - 三角函数:
sinf、cosf、sinpif、cospif、sincosf、sincospif计算正弦、余弦、及其在 π 倍数上的变种。 - 对数与指数函数:
logf、log2f、log10f、expf、exp2f、exp10f用于自然对数、以 2 或 10 为底的对数,及对应的指数运算。 - 反三角函数:
atanf、asinf、acosf返回反正切、反正弦、反余弦函数的值。 - 数学常用操作:
fmodf用于取余,fabsf返回绝对值,fminf和fmaxf用于选择最小值和最大值。
稍快,但不完全精确的 __sinf
两个下划线的 __sinf 是 GPU intrinstics,精度相当于 GLSL 里的那种。适合对精度要求不高,但有性能要求的图形学任务。
#include <cuda_runtime.h>
#include <cstdio>
#include <vector>
#include "CudaAllocator.h"
#include "helper_cuda.h"
#include "ticktock.h"
template <class Func>
__global__ void parallel_for(int n, Func func) {
for (int i = blockDim.x * blockIdx.x + threadIdx.x; i < n;
i += blockDim.x * gridDim.x) {
func(i);
}
}
int main() {
int n = 1 << 25;
std::vector<float, CudaAllocator<float>> gpu(n);
std::vector<float> cpu(n);
TICK(cpu_sinf);
for (int i = 0; i < n; i++) {
cpu[i] = sinf(i);
}
TOCK(cpu_sinf);
TICK(gpu_sinf);
parallel_for<<<n / 512, 128>>>(
n, [gpu = gpu.data()] __device__(int i) { gpu[i] = __sinf(i); });
checkCudaErrors(cudaDeviceSynchronize());
TOCK(gpu_sinf);
// for (int i = 0; i < n; i++) {
// printf("diff %d = %f\n", i, gpu[i] - cpu[i]);
//}
return 0;
}
// cpu_sinf: 0.118834s
// gpu_sinf: 0.026515s
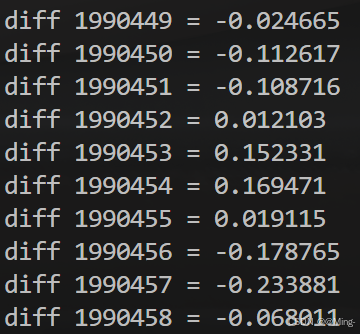
类似的低精度内建函数还有 __expf、__logf、__cosf、__powf 等.
另外,__fdividef(x, y) 是一个专门用于浮点除法的优化函数,它提供与常规除法相同的精度,且计算速度更快。然而,当 y 的值位于 2^216 到 2^218 之间时,可能会返回错误的结果,因此在使用时需要避免该数值范围。

编译器选项:--use_fast_math
启用 --use_fast_math 选项时,编译器会对多个数学操作进行优化以提升性能,具体包括:
sinf调用优化:所有对sinf的调用会自动替换为__sinf,以使用更快的实现。--ftz=true:将极小数(非规格化数,denormal)视为 0,从而避免额外的处理开销,提高运算速度。--prec-div=false:降低除法运算的精度,换取更快的计算速度。--prec-sqrt=false:降低平方根运算的精度,提升运算速度。--fmad:启用浮点数乘加指令(FMA),将表达式a * b + c自动优化为更高效的乘加指令。此选项默认开启,因其对性能影响显著。
开启 --use_fast_math 后,以上所有优化选项将自动启用。
SAXPY(Scalar A times X Plus Y)
即标量 A 乘 X 加 Y
这是很多CUDA教科书中的“Hello, world”,我们这里也来实现一下:
#include <cuda_runtime.h>
#include <cstdio>
#include <vector>
#include "CudaAllocator.h"
#include "helper_cuda.h"
template <class Func>
__global__ void parallel_for(int n, Func func) {
for (int i = blockDim.x * blockIdx.x + threadIdx.x; i < n;
i += blockDim.x * gridDim.x) {
func(i);
}
}
int main() {
int n = 65536;
float a = 3.14f;
std::vector<float, CudaAllocator<float>> x(n);
std::vector<float, CudaAllocator<float>> y(n);
for (int i = 0; i < n; i++) {
x[i] = std::rand() * (1.f / RAND_MAX);
y[i] = std::rand() * (1.f / RAND_MAX);
}
parallel_for<<<n / 512, 128>>>(
n, [a, x = x.data(), y = y.data()] __device__(int i) {
x[i] = a * x[i] + y[i]; // 乘加操作
});
checkCudaErrors(cudaDeviceSynchronize());
for (int i = 0; i < n; i++) {
printf("x[%d] = %f\n", i, x[i]);
}
return 0;
}





















 646
646

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








