多尺度（有限元）降阶模型下的DNN方法

多尺度模型的DNN解法

今天，想和大家分享的是Eric Chung的三篇文章。Deep Multiscale Model Learning、Deep Global Model Reduction Learning、Prediction of Discretization of GMsFEM using Deep Learning。

Eric是港中文（The Chinese University of Hong Kong ）的一个教授，曾经也来访过我们所做过报告，它的工作主要是关于CFD的。

某种意义上来说，这三篇文章是“一样”的。我会比较详细地介绍第一篇文章，后面的，我只会介绍不同的地方。

这里仍然有许多我不懂的地方，在我读文章的时候，毕竟，我对多尺度方法知之甚少。

NLMC&DNN（DMML，Deep Multiscale Model Reduction Learning）

众所周知，DNN可以表示一个非线性函数，我们所在意的是输入是什么，输出是什么，DNN的结构是什么，以及我们用来训练网络的数据。

在第一篇文章中，作者使用NLMC作为多尺度模型，NLMC是non-local multi-continuum approach的缩写。它定义了一个新的基函数，以使得自由度有了物理意义，什么物理意义呢？那就是“解的平均”。

在另一方面，我们可以将DNN用来求解PDE和进行模型的约化。

在这篇文章中，作者联合了两种方法学，制作了一个DNN网络，和多尺度模型约化概念相关。这个大大减小了计算复杂度。另外，作者还比较了用不同比例（proportion）的观测数据和计算数据用于训练的结果。

OK，让我们开始这一部分。

一般来说，我们研究：

这里的$I$表示输入，包括介质属性：渗透场（permeability field）、源项（well rates），初始条件。

考虑一个特殊的情况，就是一个特殊的扩散方程，如下：

它的边界条件是零纽曼边界条件，即$\nabla u\cdot n=0$。

使用标准的有限元方法，时间离散上，采用后向欧拉格式（backward Euler），我们可以得到：

这里的下标（subscript）$f$表示细网格上的细尺度（fine-scale）解。
写成矩阵的形式，我们有：

$M_f$表示质量（mass）矩阵，$A_f$表示刚度（stiffness）矩阵，$b_f$是右手边的那个向量。

以上说的是，经典的有限元方法。什么是NLMC？

我们将区域D分割为matrix region和fractures region。即：

这里，这些符号在原文中的解释是：

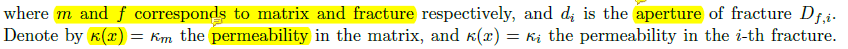
我并不是太明白这个，特别是什么是$d_i$。接下来，我们定义oversampling of 粗网格单元 $K_i$ as $K_i^{+}$。

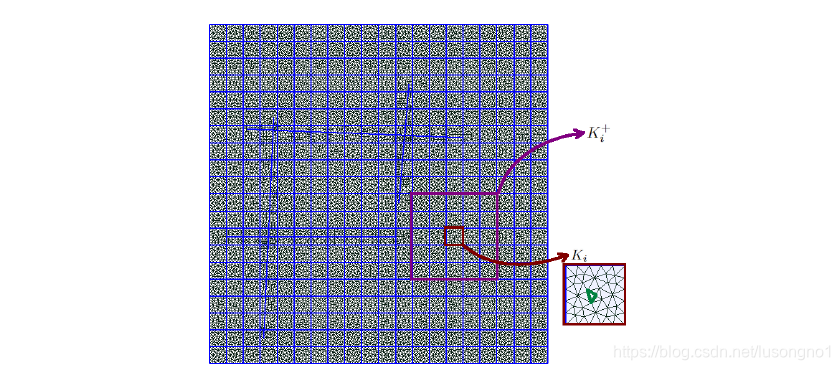
然后，我们可以得到基函数${\psi }_m^{(i)}$，通过求解如下一个约束（constraint）极小化问题：

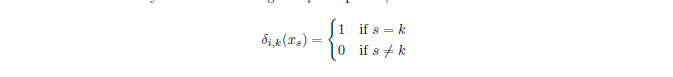
定义传递（transmissbility）矩阵T，如下：

写成如下形式：

最后我们可以得到NLMC的一个upscale model：

NLMC的优点在于，其一是我们能得到一个更精确的解，其二，粗网格解有重要的物理意义，也就是块中的平均压力。

下面，我将介绍，如何联合NLMC方法和DNN。

首先，使用NLMC方法去求解问题得到解：

我们的目标是得到一个DNN，写成如下：

这里的$I^n$是一些输入参数，比如说源项等。

可以使用之前得到的解去训练网络。这里花写的$N$，在每一个时刻（time instant）可以是相同：

也可以是不同的：

我们也可以从影响域（region of infulence）中去寻找神经网络的输入，它告诉了我们合适的输入变量的数目。传递矩阵（tansmissibility）给了我们一些信息关于粗参数直接的连接。

我不是特别清楚怎么做的。但是，In a word， NLMC模型的影响域给我们提供了一些连接信息关于神经网络，并且减少了神经网络的复杂度且提供了一个好的初始的权重矩阵，如图所示：

在这篇文章中，作者还试图加入”观测数据“来改进这个降阶模型。所谓的观测数据，主要来自于：1、pertburb仿真数据；2、perturb渗透率（permeability），重跑仿真得到数据；3、可得到的实验数据。

一般来说，观测数据是非常难以得到的。所以，作者综合仿真数据和观测数据来训练神经网络，包括：观测数据only，仿真数据only，两者混合。

结论是，incorporating观测数据在训练中会改进结果，incorporating一些计算数据会改进预测。

POD&DNN（Proper Orhogonal Decomposition）

接下来，我要介绍得是第二篇文章。许多东西和第一篇文章是一样的，我只介绍不一样的地方。

我们考虑的模型问题是，在区域$\Omega =[0,1{]}^2$中，考察方程：

在我们的仿真中，我们会考虑一种指数模型，$\kappa (x,u)=\kappa (x)\text{exp}(\alpha u)$，这里的$u$是流体的压力，$g$是个时间依赖（time-dependent）的源项，$\alpha$是一个非线性参数。在这项工作中，作者考虑渗透（permeability）场包含wavelet-like的通道，如图：

通过标准的有限元方法，时间离散上，依然采用隐式（implicit）欧拉，我们能得到：

写成矩阵的形式，为：

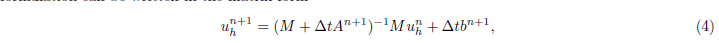
下面，我们开始做MOR（model order reduction）通过POD（Proper Orhogonal Decomposition）。

考虑N个instantaneous snapshots：

对$\Phi$做奇异值分解（SVD）有：

这里的$C={\Phi }^T\Phi$，${\sigma }_j$是奇异值，$w_j$是右奇异向量，${\xi }_j$是左奇异向量。

选择前m大的奇异值对应的左奇异特征向量，形成一个新的子空间$W_h\subset V_h$，我们成之为POD子空间。你们还记得PCA降维（dimensionality reduction ）？同一个思想对吧。

然后我们做一个投影到POD子空间上，我们的到原问题的逼近：

找一个${\tilde{u}}_h^{n+1}\in W_h$，使得：

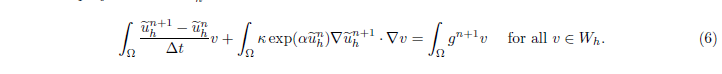
下面我们来构建节点基函数，做${\xi }_j$的线性组合，那么节点基函数可以表示为：

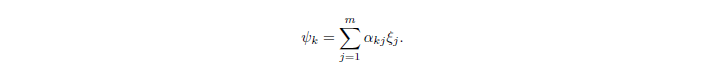
POD子空间中解的逼近就可以表示为：

那么在降阶模型中，解的矩阵表达可以写为：

剩下的部分和第一篇论文讨论的是一样的，只不过没有所谓的“religion of influence”。

GMsFEM&DNN（Generalized Multiscale Finite Element Methods）

最后一篇介绍的论文是关于GMsFEM（Generalized Multiscale Finite Element Methods）的DNN方法。

考虑问题：

通过经典的有限元方法，我们可以得到：

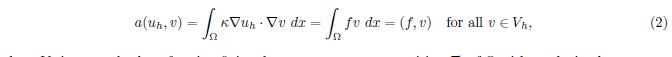
为了获得某些重要的信息，网格尺度$h$需要足够小，这造成了巨大的计算消耗。Generalized Multiscale Finite Element Method (GMsFEM)做了一个模型的约化，通过减少自由度的数目（degree of freedom）。

由于时间关系，这里我们只需要知道GMsFEM是一种模型约化技术，和前面提到的POD、NLMC是相同的意思。

通过一些我们跳过的推导，最终我需要寻找多尺度解$u_{ms}\in V_{ms}$，使得：

写成矩阵的形式：

通过downscaling算子R，我们能得到多尺度解的fine-scale表示，即：

由于模型的uncertainties，计算消耗是个大问题。我们可以利用DNN和已有的数据来减少计算消耗。

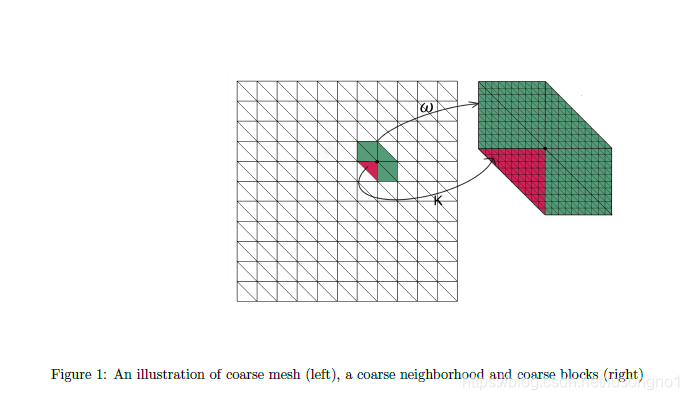
如图所示：

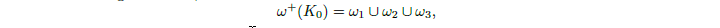
这里的${\omega }_1,{\omega }_2,{\omega }_3$表示$K_0$的3个neighborhoods block。

定义多尺度基函数和local coarse-scale刚度矩阵如下：

$\kappa$是permeability场。我们感兴趣的是构建（constructing）映射$g_B^{m,i}$和$g_M^l$，

我们用两个网络来表示这两个映射，

联合上述我所说的，我们可以得到downscale算子$R$，form the线性系统，以及得到最后的多尺度解。

通过训练网络，我们可以得到神经网络对那两个映射的逼近：

一旦神经网络建好了，我们可以组装得到的局部刚度矩阵$A_c^{K_l,pred}$得到全局矩阵的预测$A_c^{pred}$，然后求解如下线性系统：

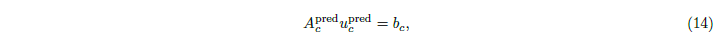
通过组装（Assemble）得到的基函数，得到downscaling算子。从而，得到预测的多尺度解：

作者也做了一些数值实验。