Linear regression with one variable 单参数线性回归
1.Model representation
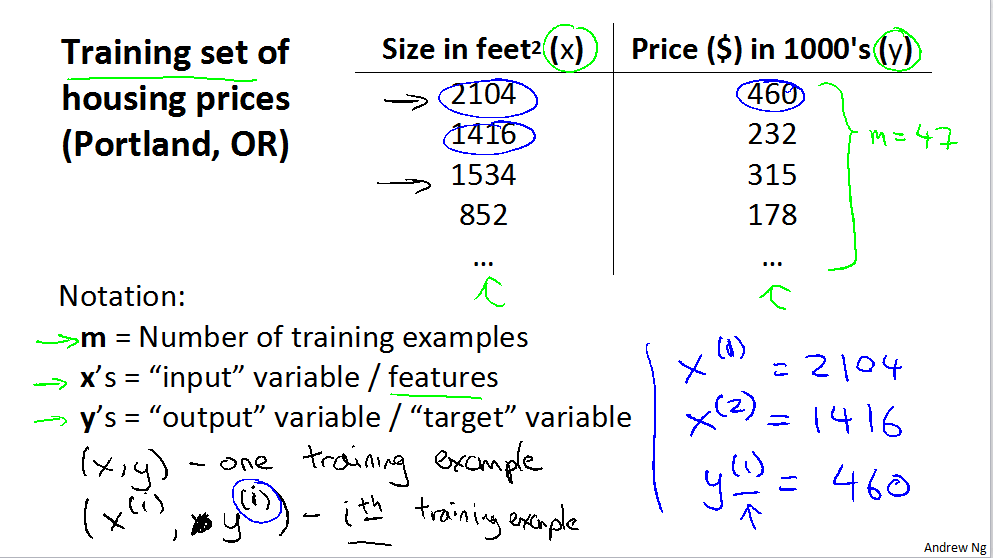
引例:一个房屋尺寸与对应定价的数据集,其中记x 为房屋尺寸,y 为房屋售价(x,y)为一个训练数据。另外m为训练数据集训练数据的数量,i为第i个数据集的索引,当做第i个数据的上标,Eg: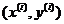
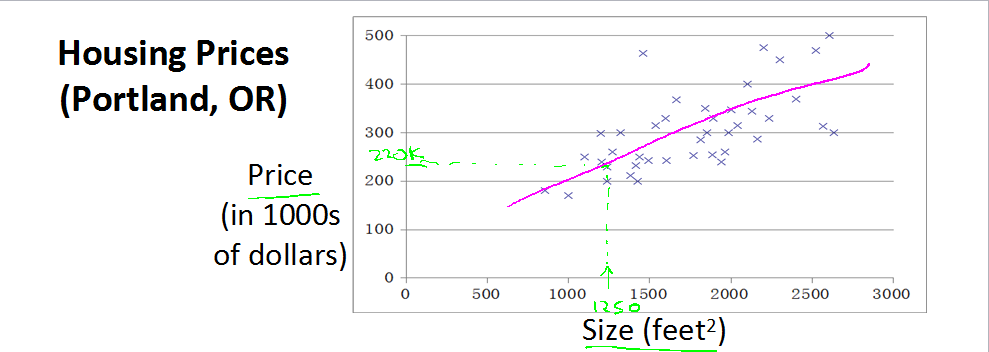
训练数据集在坐标轴中表示如下:
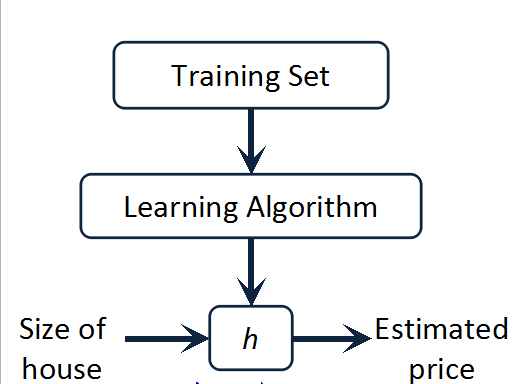
线性规划问题流程图:
But ,how do we represent h ?
2.Cost function
对于单因子线性规划通常令
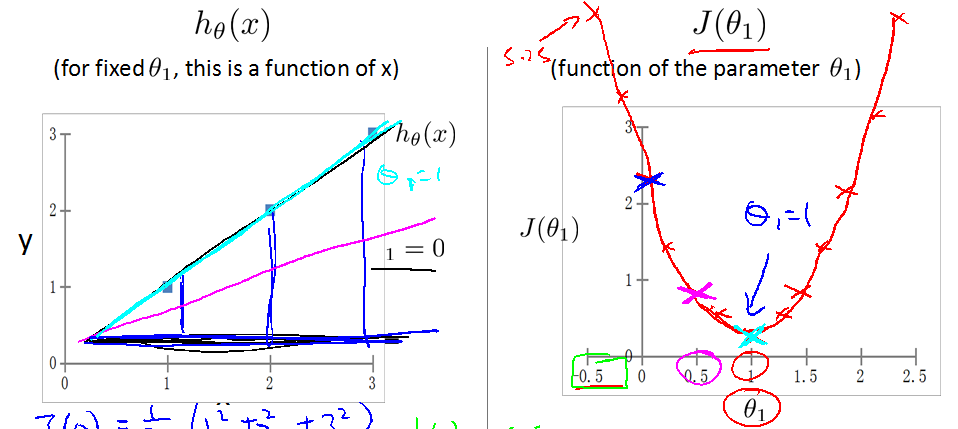
对于不同的
但是,对于一个问题我们要怎么得到合适的
其中:
只考虑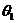
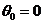

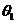
当
得到的
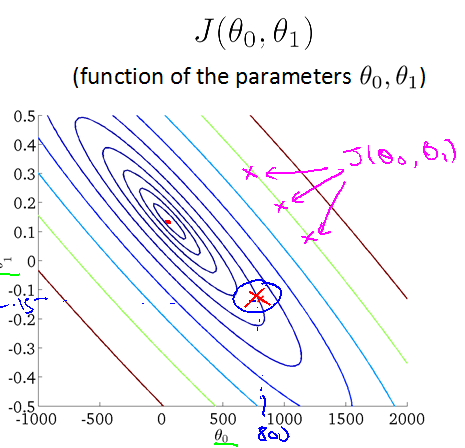
用等高线表示如下图:
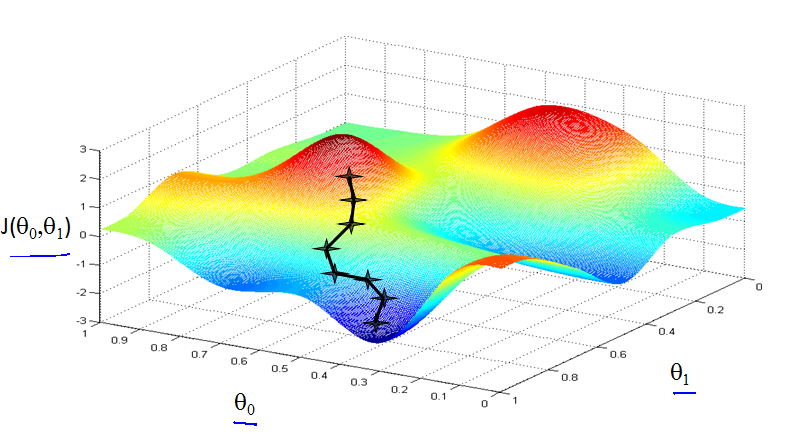
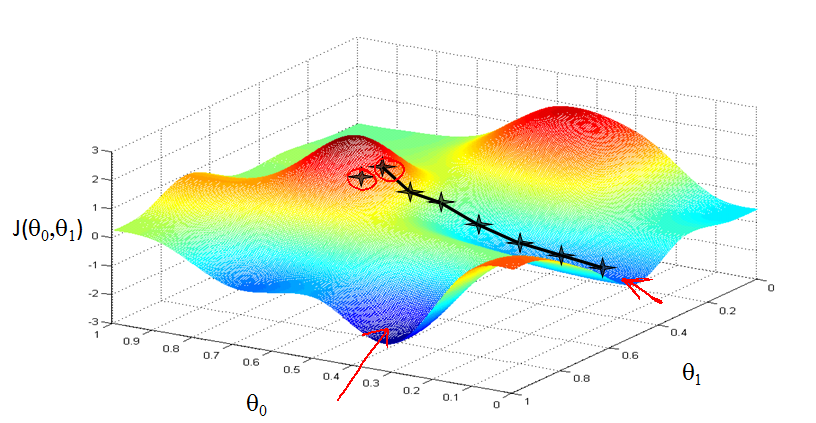
3.Gradient descent
如何得到

设定一个初始的







其中:


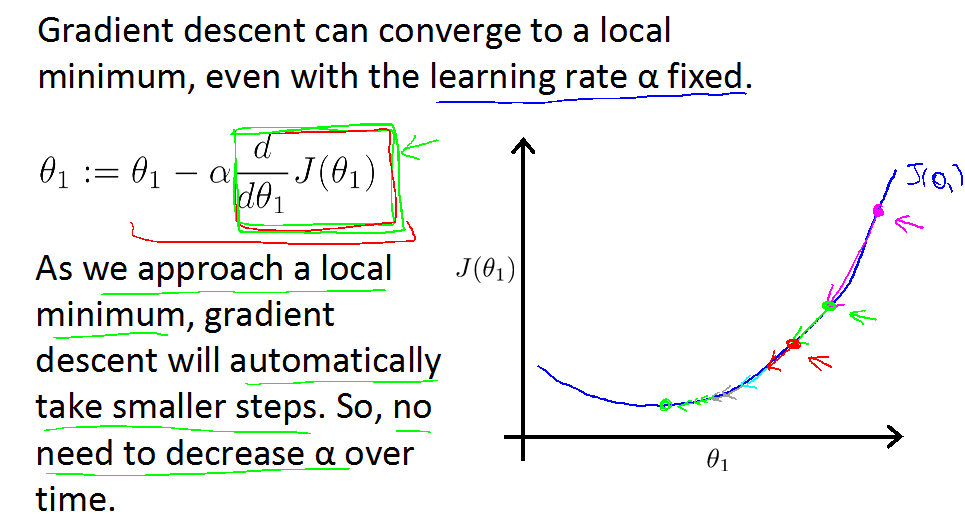
下图为当梯度大于0和小于0时算法的工作情况。




若
若
在

由上面两张图片可以得到:
课程资源









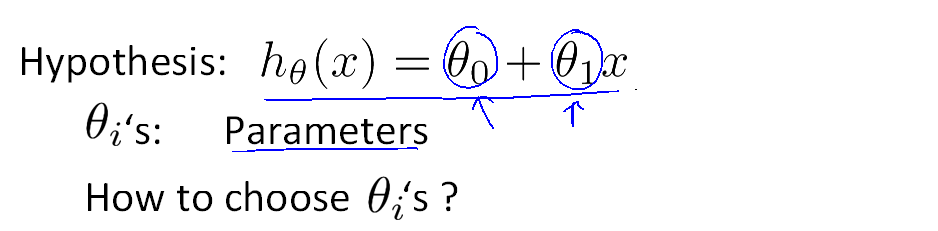






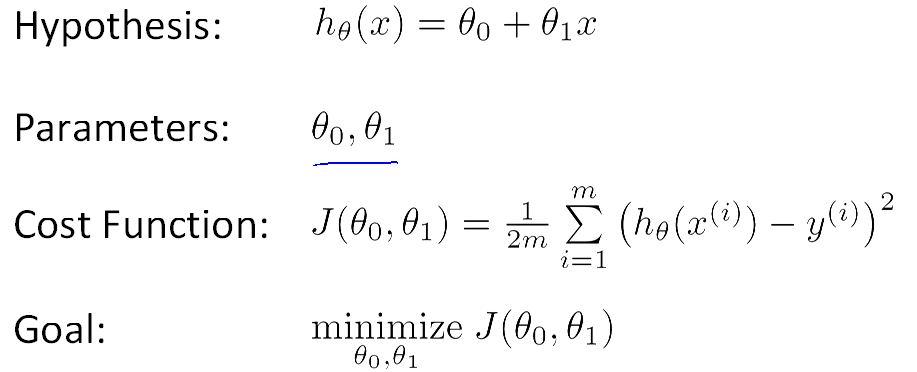



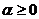


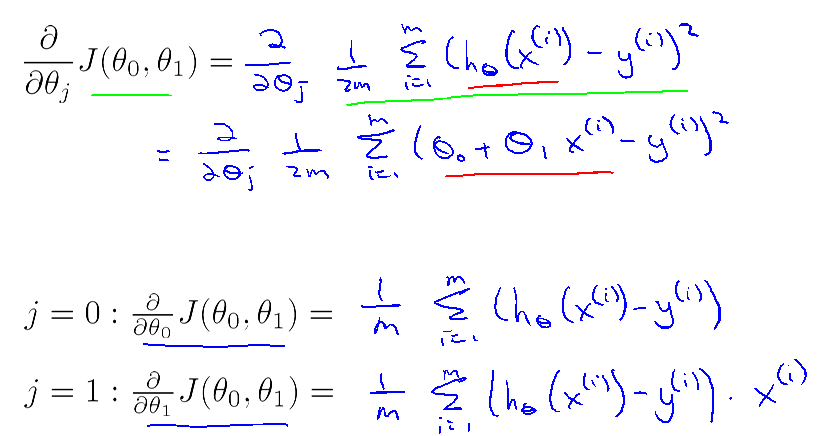















 165
165

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








