坐标变换
已知b1, b2 为新的基向量。A为基变换矩阵。
- 变换矩阵怎么来的?
对于e1,e2而言,实际上就是b1,b2本身。 - 变换矩阵 乘上 新的基向量下的坐标 的意义是什么?
是原基向量下的坐标。所以变换矩阵的意义就在于此。

主成分分析
它主要是以“提取出特征的主要成分”这一方式来实现降维的。
如下所示一矩阵。
-
n行的特征,m列的样本。
[ x 1 , x 2 , . . . , x m ] = [ x 11 x 12 ⋯ x 1 m x 21 ⋮ ⋮ ⋮ x n 1 ⋯ ⋯ x n m ] \left[ x_1,x_2,...,x_m \right] =\left[ \begin{matrix}{} x_{11}& x_{12}& \cdots& x_{1m}\\ x_{21}& & & \vdots\\ \vdots& & & \vdots\\ x_{n1}& \cdots& \cdots& x_{nm}\\ \end{matrix} \right] [x1,x2,...,xm]=⎣ ⎡x11x21⋮xn1x12⋯⋯⋯x1m⋮⋮xnm⎦ ⎤ -
对每一个特征进行零均值化。就是把每个数减去该行的均值,得到一个新的矩阵。(这是为了对特征一视同仁)
-
求协方差矩阵。
c o v ( X , Y ) = E ( ( X − E ( X ) ) ( Y − E ( Y ) ) ) cov\left( X,Y \right) =E\left( \left( X-E\left( X \right) \right) \left( Y-E\left( Y \right) \right) \right) cov(X,Y)=E((X−E(X))(Y−E(Y)))
由于之前已经经过零均值化处理,所以
c o v ( X , Y ) = E ( X Y ) = 1 n ∑ 1 n x i y i cov\left( X,Y \right) =E\left( XY \right) =\frac{1}{n}\sum_1^n{x_iy_i} cov(X,Y)=E(XY)=n11∑nxiyi
而协方差矩阵如下,注意是特征与特征的比较,也就是行与行的比较。
[ c o v ( x 1 , x 1 ) c o v ( x 1 , x 2 ) ⋯ c o v ( x 1 , x n ) c o v ( x 2 , x 1 ) ⋮ ⋮ ⋮ c o v ( x n , x 1 ) ⋯ ⋯ c o v ( x n , x n ) ] = 1 n X X T \left[ \begin{matrix} cov\left( x_1,x_1 \right)& cov\left( x_1,x_2 \right)& \cdots& cov\left( x_1,x_n \right)\\ cov\left( x_2,x_1 \right)& & & \vdots\\ \vdots& & & \vdots\\ cov\left( x_n,x_1 \right)& \cdots& \cdots& cov\left( x_n,x_n \right)\\ \end{matrix} \right] =\frac{1}{n}XX^T ⎣ ⎡cov(x1,x1)cov(x2,x1)⋮cov(xn,x1)cov(x1,x2)⋯⋯⋯cov(x1,xn)⋮⋮cov(xn,xn)⎦ ⎤=n1XXT -
求出协方差矩阵的特征值和特征向量,将特征值从大到小排列,特征向量依次对应(特征向量要标准化)。
怎么特征分解可以看我这篇博客 -
取前k行组成新的矩阵P。
-
Y = PX,得到的Y就是新的降维的矩阵。相当于P是一个降维矩阵,是将X投影到低维度上。
解释一下为什么协方差矩阵的特征值越大,越能成为主成分。
1)在信号处理中认为信号具有较大的方差,噪声有较小的方差。如果样本在X上的投影方差较大,在Y上的投影方差较小,那么可认为Y上的投影是由噪声引起的。
2)方差越大,数据越分散,也就意味着信息量越多,信号越强,也可以说熵越大,该特征越有区分度。协方差代表维度x和维度y之间的相关程度,协方差越大,也就意味着噪声越大,信息的冗余程度越高。
因此n维的数据降低到k维,在k维上的每一维的样本方差都很大。
贝叶斯决策
- 贝叶斯公式
P ( B i ∣ A ) = P ( B i ) P ( A ∣ B i ) P ( A ) = P ( B i ) P ( A ∣ B i ) ∑ j = 1 n P ( A ∣ B j ) P ( B j ) P\left( B_i|A \right) =\frac{P\left( B_i \right) P\left( A|B_i \right)}{P\left( A \right)}=\frac{P\left( B_i \right) P\left( A|B_i \right)}{\sum_{j=1}^n{P\left( A|B_j \right) P\left( B_j \right)}} P(Bi∣A)=P(A)P(Bi)P(A∣Bi)=∑j=1nP(A∣Bj)P(Bj)P(Bi)P(A∣Bi)
- P(A),P(B):事件A、B的先验概率。
- P(A|B),P(B|A):事件A,B的后验概率。
- P(A|B)/ P(A) :调整因子。
- 贝叶斯决策:扔进去一个先验概率P(B),若调整因子大于1,P(B)变大,若小于1,P(B)变小,实际上是利用已知的信息(后验概率)起到对B的一个修正的作用,
最小错误率贝叶斯决策
- 最小错误率———错误的概率最小———正确的概率最大。
- 对二类决策问题,假设可以分成w1,w2两类。x表示样本,错误率为e。决策在x样本上的错误率:
P ( e ∣ x ) = { P ( w 2 ∣ x ) x ∈ w 1 P ( w 1 ∣ x ) x ∈ w 2 P\left( e|x \right) =\begin{cases} P\left( w_2|x \right) \,\,x\in w_1\\ P\left( w_1|x \right) \,\,x\in w_2\\ \end{cases} P(e∣x)={P(w2∣x)x∈w1P(w1∣x)x∈w2 - 一个类的错误率等于另一个类的正确率。那其实可以认为:
若 P ( w 1 ∣ x ) > P ( w 2 ∣ x ) 则 x ∈ w 1 ; 否则 x ∈ w 2 \text{若}P\left( w_1|x \right) >P\left( w_2|x \right) \text{则}x\in w_1;\text{否则}x\in w_2 若P(w1∣x)>P(w2∣x)则x∈w1;否则x∈w2
最小风险贝叶斯决策
- 最小风险:决策的错误带来的损失最小!
- 损失:需要把不同决策看成行,真实的状态看成列,创建一个损失决策表(一般专家才能给出),实际上就是定义不同的损失函数。
- 怎么决策:让损失最小,最小化期望风险。
朴素贝叶斯分类
-
朴素:各个特征相互独立,满足属性条件独立性假设。
-
样本x属于yk类的后验概率 P ( y k ∣ x ) = P ( y k ) P ( x ∣ y k ) P ( x ) P\left( y_k|x \right) =\frac{P\left( y_k \right) P\left( x|y_k \right)}{P\left( x \right)} P(yk∣x)=P(x)P(yk)P(x∣yk)
-
P(yk)可由训练样本集中该类样本出现的频率来估计
-
P(x)样本的概率,与类别无关,可以直接算。
-
P(x|yk)可由yk类内属性为x的样本的比例来估计。
-
看下面这个式子就可以明白了。训练集会告诉你右边式子的所有的概率。
-
先把嫁的筛选出来,再求不帅的频率

图片来源 -
有些概率逼近于0怎么办。
扩大样本容量:增加m个等效样本。得到新的类条件概率:(ni是yk类内样本xi的个数,p为之前的概率)
P ( x i ∣ y k ) = n i + m p n + m P\left( x_i|y_k \right) =\frac{n_i+mp}{n+m} P(xi∣yk)=n+mni+mp
参数估计
估计量的评价
-
无偏性
E ( θ ~ ) = θ E\left( \widetilde{\theta } \right) =\theta E(θ )=θ
可以这么理解,题目证明:某样本统计值是总体统计值的无偏估计量。
E套进去。例如,证明样本均值是期望u的无偏估计量。
E ( X ˉ ) = E ( 1 n ∑ i = 1 n E ( X i ) ) = 1 n ∑ i = 1 n μ = μ E\left( \bar{X} \right) =E\left( \frac{1}{n}\sum_{i=1}^n{E\left( X_i \right)} \right) =\frac{1}{n}\sum_{i=1}^n{\mu}=\mu E(Xˉ)=E(n1i=1∑nE(Xi))=n1i=1∑nμ=μ -
有效性
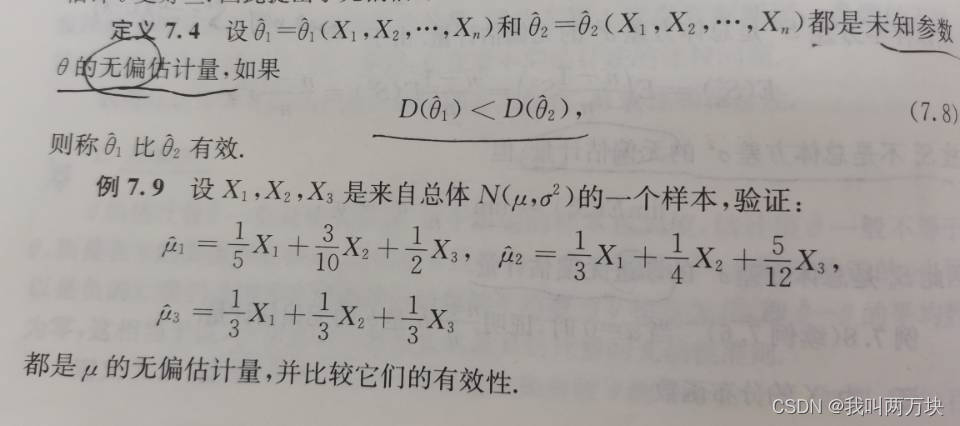
点估计
矩估计
样本K阶原点矩收敛于期望
1
n
∑
i
=
1
n
X
i
k
=
E
(
X
k
)
\frac{1}{n}\sum_{i=1}^n{X_{i}^{k}=E\left( X^k \right)}
n1i=1∑nXik=E(Xk)
最大似然估计
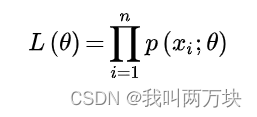
对L()取对数,然后求导,然后导数等于0,因为要求最大值。以此估计。
最小二乘估计
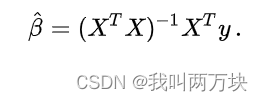





















 758
758











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








