647. 回文子串
-
1. 暴力穷举 , i 遍历 [0, N) , j 遍历 [i+1, N] ,判断每一个子串 s[i, j) 是否是回文串,判断是否是回文串可以采用 对撞指针 的方法。如果是回文串就计数 +1 。

上面代码中判断子串是否是一个回文串的方法的时间复杂度最坏是O(N),所以加上外面的2层for循环,总的时间复杂度是O(N^3)。
-
2. 中心扩展法 , 每次选择一个 中心 向 左右 扩展到不能扩为止,
-
可以先实现这样一个 函数 centerAround(s, L, R) , 它在 每次 L 和 R 执行 左右扩展 时,进行 1次 计数 统计 ,即如果 左右字符相等 ,则 计数+1 , 不相等 就停止。
-
由于存在 奇数 回文串和 偶数 回文串,所以我们遍历每个字符位置 i ,对于 奇数 回文串: L 和 R 都从中心 i 开始向左右扩展,即调用一次 centerAround(s, i, i) ,对于 偶数 回文串: L 从 i , R 从 i+1 开始向左右扩展,即调用一次 centerAround(s, i, i+1) 。
-
这样遍历完每个位置,并将每次扩展的计数 累加 起来返回即可。
-
中心扩展法的实现也可以参考 在【 字符串篇 】中的 【 5. 最长回文子串 】 题。

-
3. 动态规划 ,定义 dp[i][j] 表示 s [i , j] 的子串 是否是回文串 ,初始化二维 dp 表中 对角线 上的为 true , 因为只有 1个 字符肯定是回文。
-
如果区间 [i , j] 只有 2个 字符,则 dp[i][j] = s[i] == s[j] ,
-
如果区间 [i , j] 上 有 > 2个 字符,看 s[i] 是否等于 s[j] :
-
1)如果 s[i]==s[j] , 则 s[i, j] 是否是回文还需看里面一层即 s[i + 1, j - 1] 是否是回文,所以此时 dp[i][j] = dp[i + 1][j - 1] ,
-
2)如果 s[i] != s[j] , 则 s[i, j] 不是回文,此时 dp[i][j] = false 。
-
因为 dp[i][j] 的值在计算时可能用到 前一列 的值,所以遍历求解时,需要先遍历列下标 j 从 [1, N) , 再遍历行坐标 i 从 [0, j) ,这里只需遍历到 i < j 即表中 上半 部分,对应区间 [i, j] 范围。
-
在每次更新 dp[i][j] 之后,判断一下如果 dp[i][j] 值为 true , 就将答案 计数+1 即可。


本题属于典型的【范围尝试模型】。
5. 最长回文子串

-
1. 中心扩展法 ,请参考 【 字符串篇 】的该题题解。
-
2. 动态规划 ,同 647. 回文子串 dp 解法,在每次更新 dp[i][j] 之后,如果 dp[i][j] 为 true ,就记录最长的区间 [i, j] 的子串作为答案即可。

这里每次判断 dp[i][j] 为 true 时,如果区间长度比之前记录的答案更长,就记录下区间的起始位置点和结束位置点,而不是每次都执行 string.substring() 操作,在最后返回答案时再根据记录的这两个值进行一次字符串的截取操作,可以提高一些效率。
131. 分割回文串

-
1. DFS ,递归函数判断以 i 开头的子串 s[i...N-1] 是否可分割成回文子串,并使用 path 收集访问过的路径,最终保存到 res 中。
-
每次递归调用中,让 j 遍历 [i, N) 的每一个位置做 结尾 分割原字符串,判断如果 s[i, j] 是回文串,就将 s[i, j] 添加到 path 集合中,然后递归调用 s[j+1...] 进行处理,
-
在子递归返回后,需要做 回溯 处理,从 path 中 移除 掉 最后一个 添加的子串 。
-
递归终止: i == N ,递归深度为 N 时,将 path 添加到总结果集 res 中,返回。
-
判断 s[i, j] 是否是回文串,可以使用 对撞指针 ,不过是 O(N) 的时间复杂度。
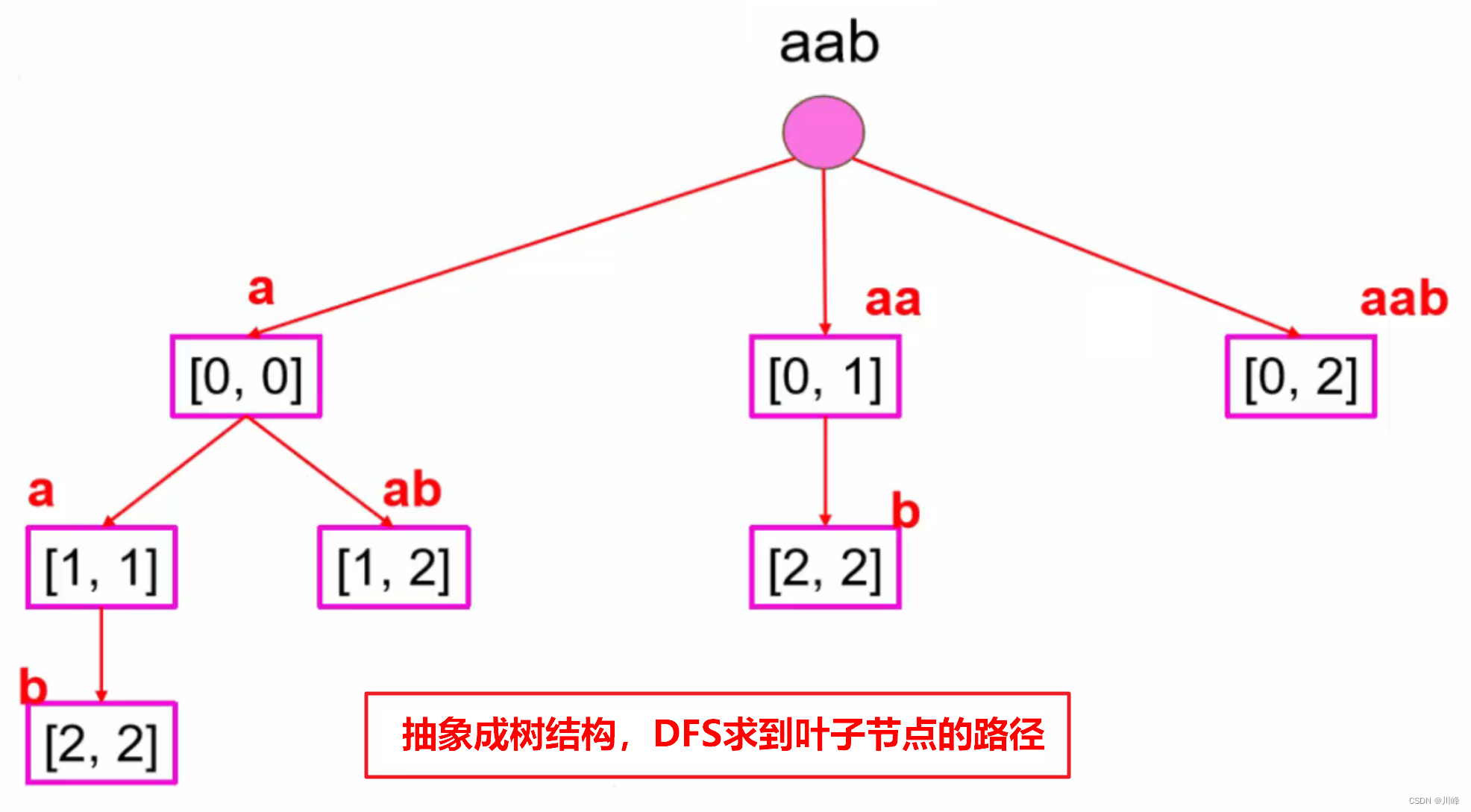
本题就是将分割的每一个子串看作是一个节点,然后收集每一条从根到叶子的节点路径,前提是这条路径上的节点对应的子串是回文串。

这个代码需要注意的是,从下一层递归返回之后,一定要进行回溯撤销操作,这里使用 Deque 作为 path 的类型是为了方便删除最后一个元素。
-
2. DFS + dp 优化 ,可以先利用【 647. 回文子串 】的代码提前求出 dp 数组,然后还是同方法1中的思路,只不过让 DFS 函数带着这个 dp 数组玩,因为有了 dp 数组之后,根据 dp 数组的含义 dp[i][j] 表示区间 s[i, j] 的子串是否是回文,这样每当需要判断 s[i, j] 是否是回文串时,就可以用 O(1) 的时间复杂度从 dp 数组中快速查找到结果,从而代替方法1中比较耗时的 isPalindrome方法。

本题也属于典型的【范围尝试模型】。
132. 分割回文串 II

-
动态规划 ,先利用【 647. 回文子串 】代码求出 dp 数组, dp[i][j] 表示子数组区间 [i, j] 对应的子串是否是回文。
-
然后定义 f[i] :表示 以 s[i] 结尾的最少分割次数 ,初始化为 系统最大值 ,遍历 [0, N) , 求出每个 f[i] 的值
-
① 如果 dp[0][i] 为 true , 说明 s[0..i] 是回文串,那么不需要分割, f[i] = 0 。
-
② 如果 dp[0][i] 为 false , 说明 s[0..i] 不是回文串, 让 j 枚举区间 [0, i) ,看 dp[j + 1][i] 的值,如果 dp[j + 1][i] 是 true , 说明 s[j+1..i] 是回文串,而此时 s[0..i] 不是回文串, 因此可以在 j 位置切一刀将 [0..i] 分成 [0..j] 和 [j+1..i] 两部分,已知 [0..j] 部分变成回文的切割次数为 f[j] , 因此只要在 f[j] 基础上再切割 1次 就得到 f[i] 了,故 f[i] = Math.min(f[i], f[j] + 1) 。
-
最后返回 f[N-1] , 即以 s[n-1] 结尾的最少分割次数。
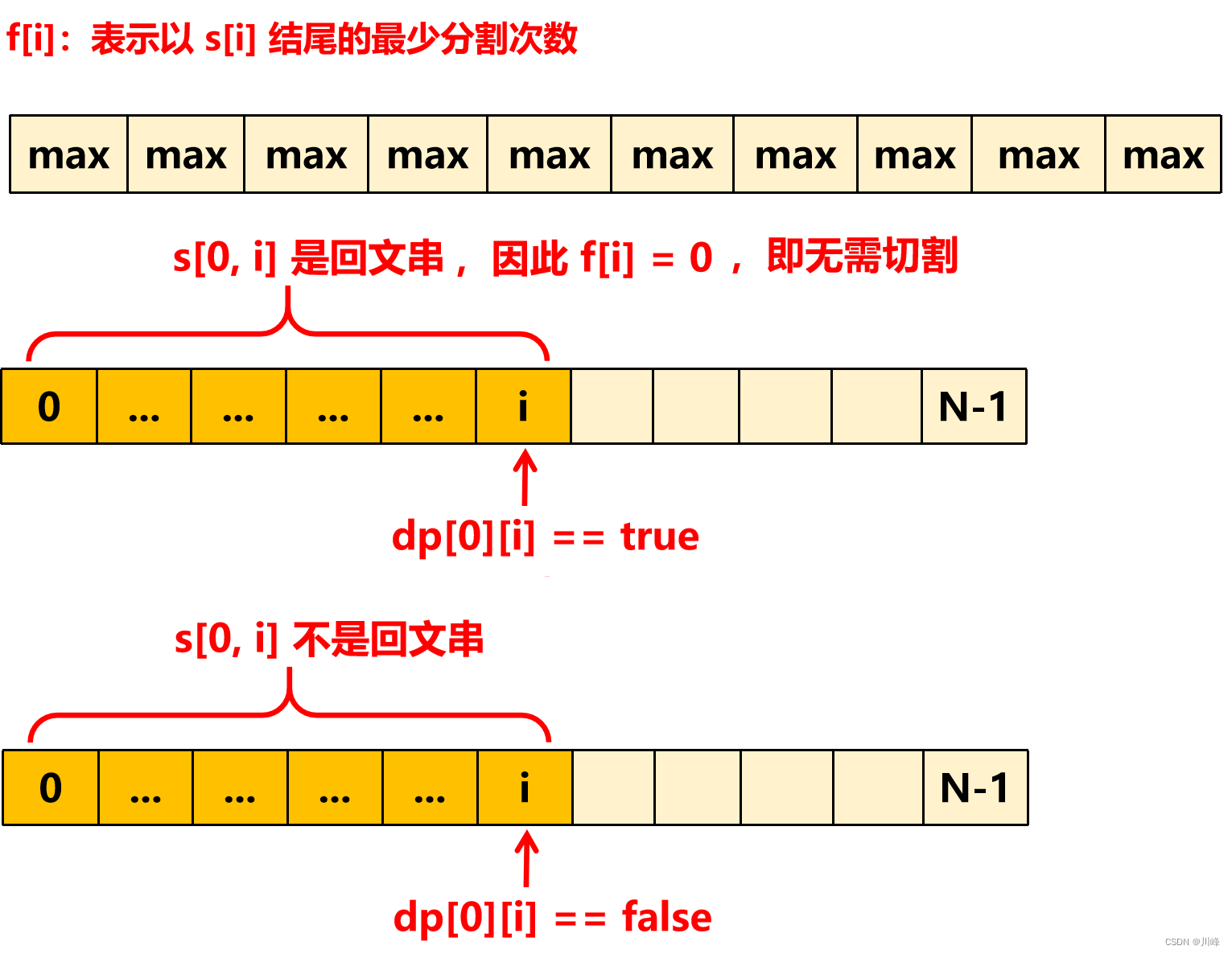
其中dp[0][i]为true的情况比较好理解,关键是dp[0][i]为false的情况,我们可以从前后面枚举 [0, i) 的每一个位置 j,直到我们找到这样一个 j 位置,它可以将s[0, i]区间分成两部分:s[0, j] 部分不是回文串,而 s[j+1, i] 部分是回文串(即dp[j+1][i]是true);因为我们是从左往右求解 f 数组的,因此当我们来到 i 位置时,s[0, j] 部分变成回文串的最少切割次数已经保存在了 f[j] 当中,所以此时我们只需在整个s[0, i]中的 j 位置再切1刀即可得到整个s[0, i]区间变成回文串的最少次数,也就是 f[j] + 1。可参考下图理解:
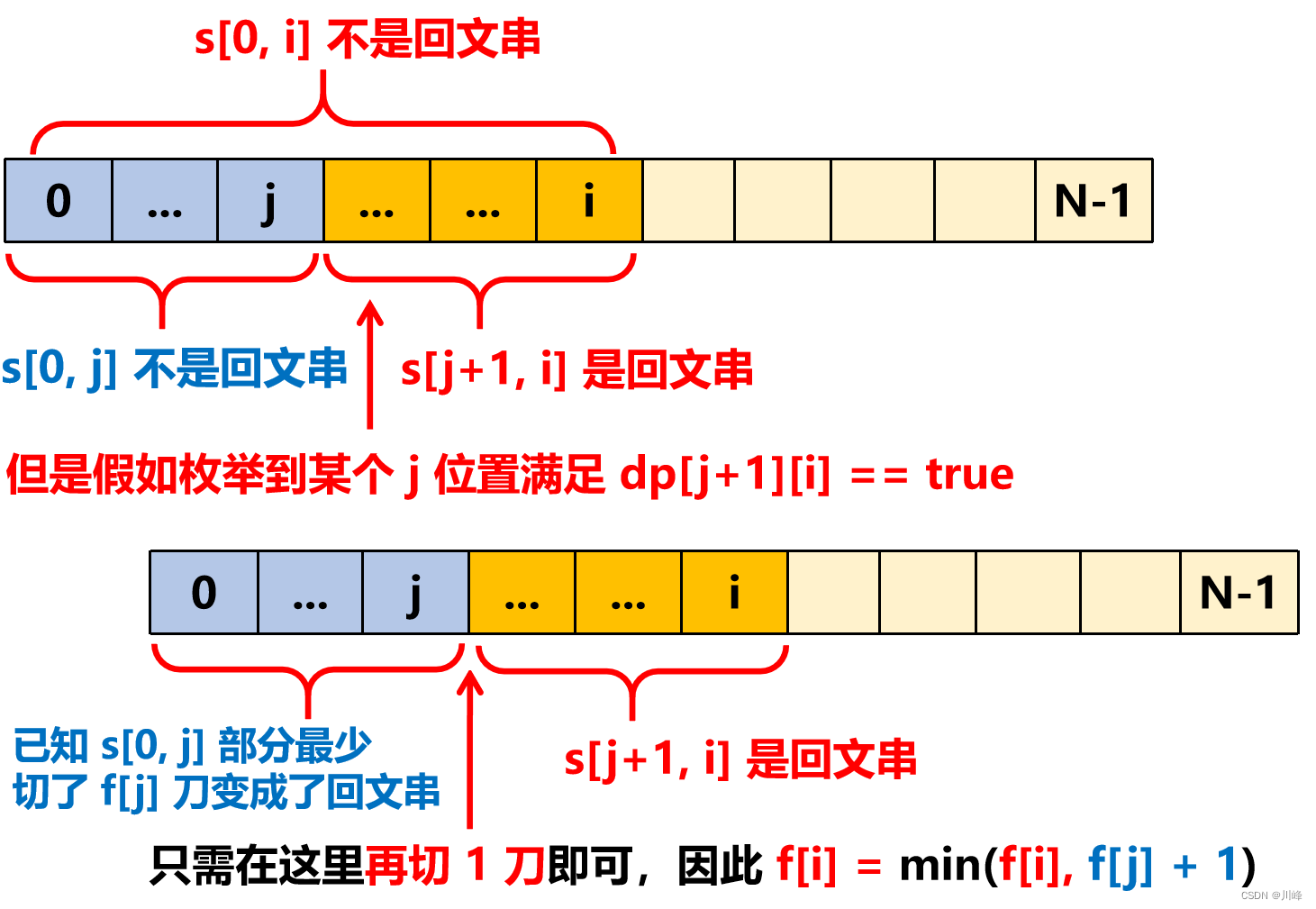
注意,这里的 j 的枚举区间是 [0, i) ,也就是 [0, i - 1],最坏的情况下 j 从 0 枚举到 i - 1 都不是回文串,但此时 s[j + 1, i] 即 s[i] 自身一个字符也可以作为回文串,所以也能保证切 1 刀一定能分割出有效的两部分回文子串。

本题也属于【范围尝试模型】,但是属于双dp,较难。注意:本题如果直接用131题的DFS代码来求min(minCount, path.size()-1)会超时。
1312. 让字符串成为回文串的最少插入次数
-
动态规划 , 定义 dp[i][j] 表示 s 的子串 s[i...j] 变为回文串 最少需要添加的字符数量 ,我们 从外向内 考虑 s[i..j] :
-
如果 s[i] == s[j] ,那么 最外层 已经形成了 回文 ,我们只需要继续考虑 s[i+1..j-1]
-
如果 s[i] != s[j] ,那么我们可以在 s[i..j] 的 末尾 添加一个 s[i] ,或者在 s[i..j] 的 开头 添加一个 s[j] ,才能使得最外层形成回文。 如果我们选择前者,需要继续考虑 s[i+1..j] ;如果选择后者,需要继续考虑 s[i..j-1] 。
-
因此我们可以得到如下的状态转移方程:
-
① if s[i] == s[j],dp[i][j] = dp[i + 1][j - 1]
-
② if s[i] != s[j], dp[i][j] = min(dp[i + 1][j] + 1, dp[i][j - 1] + 1)
-
在循环 计算 dp 值时,需要注意几点:
-
1)由于 dp 表 中某个格子的值会使用到它 下面一行 、 左边一列 以及 左下角 的 dp 值,因此必须把依赖的 dp 先计算出来,所以必须按照 从下往上 、 从左往右 的顺序进行遍历计算 dp 值。
-
2)因为是求的区间 s[i..j] 上的dp值,所以 dp 表 中只需求 上半部分 即可,即满足 i < j ,
-
3) dp 表 中 对角线 上的 i 和 j 相等 ,表示只有 1个 字符, 1个 字符不需要添加也是 回文串 ,保持默认值 0 即可。
-
所以 i 从 N-2 即 倒数第 2 行 开始往上遍历 [N - 2, 0] , 而 j 需要从 i + 1 开始( 满足 i < j ),遍历 [i + 1, N - 1] 。
-
最后返回 dp[0][N - 1] , 即 s[0..N - 1] 变为回文串最少需要添加的字符数量。
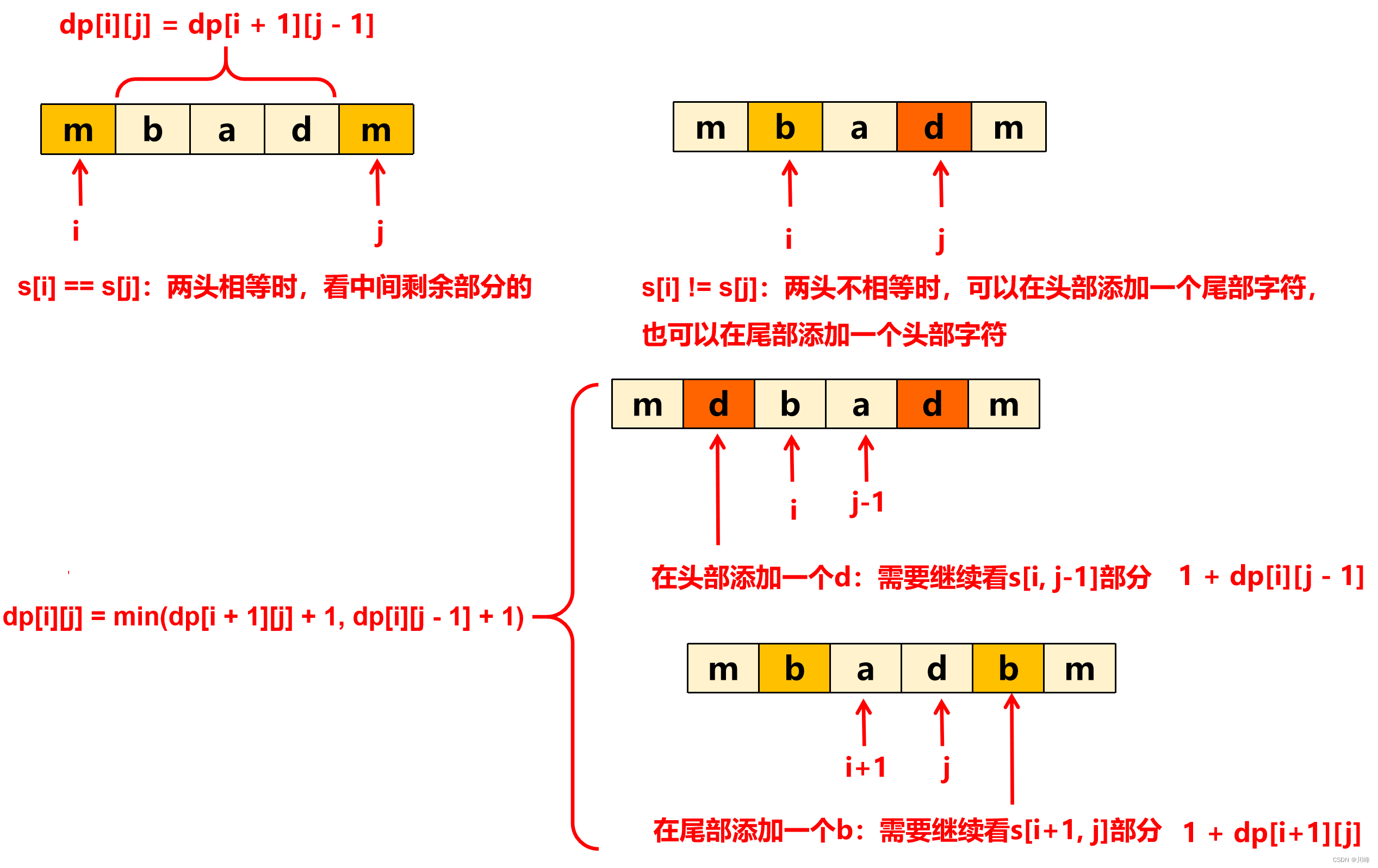
注意,这里的“添加”只是想象中的添加,并不是真的在原数组中插入数据了,因为求解dp时是遍历的原数组,而不是边遍历边插入,所以上图中添加了字符之后,可以认为 i 和 j 的位置还是在原处不动。

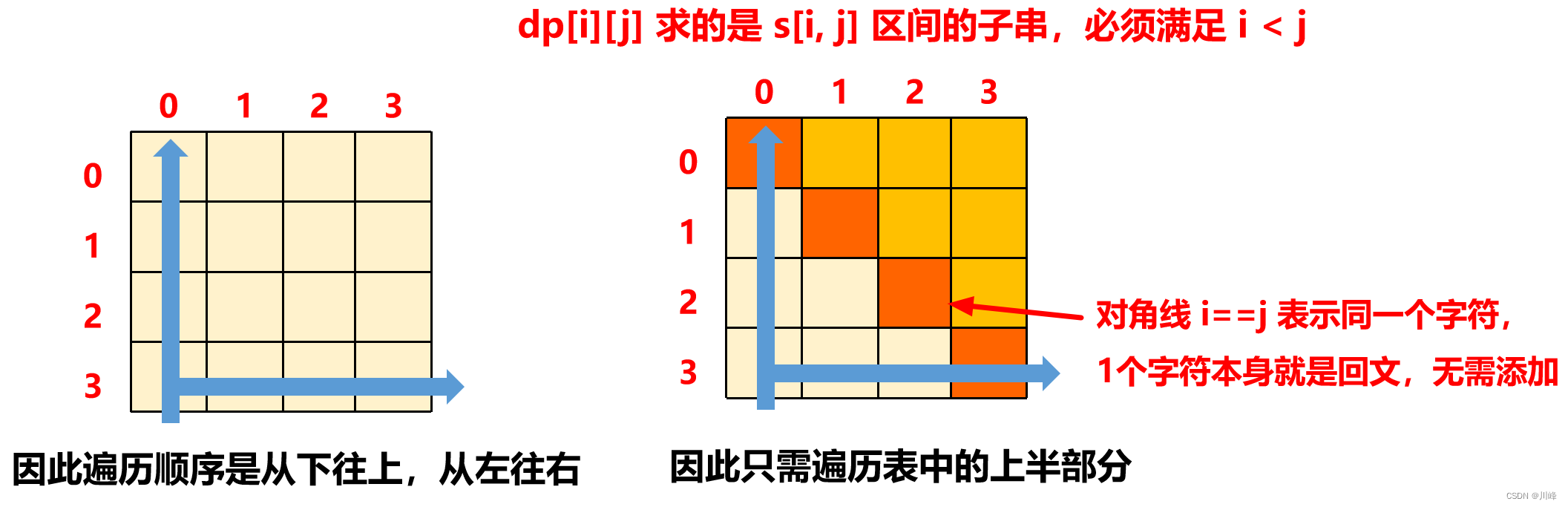

注意,代码中 i 是从 N - 2 开始遍历的,而不是 N - 1,因为 N - 1 行中只有一个对角线上的值需要处理,这里其实省略了将所有位于对角线上的 dp 值的初始化为 0 步骤,因为 dp 数组保持默认值就是








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 875
875











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










