竞赛知识点5【图论】

前言

图论起源于著名的哥尼斯堡七桥问题——从这四块陆地中任何一块开始，通过每一座桥正好
一次，再回到起点。欧拉在 1736 年解决了这个问题，欧拉证明了这个问题没有解，并且推广
了这个问题，给出了对于一个给定的图可以某种方式走遍的判定法则。这就是后来的欧拉路
径和欧拉回路。这项工作使欧拉成为图论〔及拓扑学〕的创始人。

基本概念

图的定义和分类

图是由顶点V的集合和边E的集合组成的二元组：
• 记 $G=(V，E)$
• 存在一个结点 $v$，可能含有多个前驱结点和后继结点。

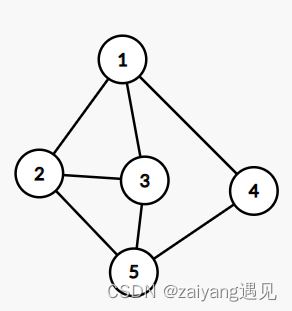
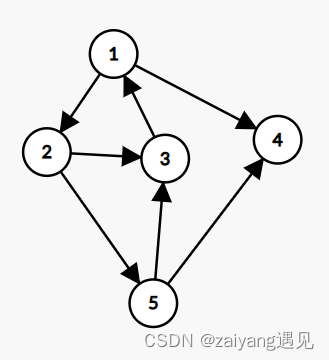
• 有向图，点与有向边的集合
• 带权图(网)，图中的边加上表示某种含义的数值，数值称为边的权
• 连通，两顶点间有路可通
• 连通图：能连成一片的图
• 连通分量：无向图中的极大连通子图

路径

在图 $G=(V，E)$中，如果对于结点 $a$ ，$b$，存在满足下述条件的结点序列 $x_1\dots \dots x_k(k>1)$
⑴ $x_1=a，x_k=b$          ⑵ $(x_i，x_{i+1})\in E(i=1‥k-1)$
则称结点序列 $x_1=a，x_2，\dots ，x_k=b$ 为结点 $a$ 到结点 $b$ 的一条路径，而路径上边的数目 $(k-1)$ 称为该路径的长度。
若起点与终点相同则为环（也叫做回路）

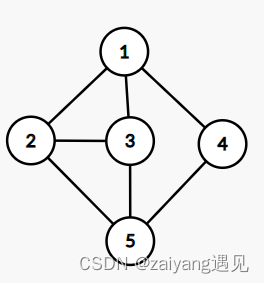
顶点的度、入度、出度

在无向图中：顶点 $v$ 的度是指与顶点 $v$ 相连的边的数目。$D(2)=3$
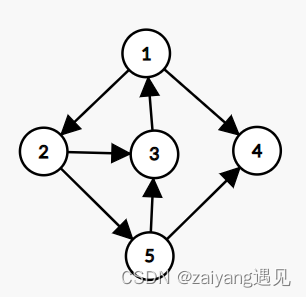
在有向图中：

• 入度，以该顶点为终点的边的数目 $ID(3)=2$
• 出度，以该顶点为起点的边的数目 $OD(3)=1$
• 度，等于该顶点的入度与出度之和。$D(5)=ID(5)+OD(5)=1+2=3$

图的存储

邻接矩阵
$map[i][j]$ 表示 $i$ 点到 $j$ 点的边权
无向图的邻接矩阵是对称的(一条无向边对应两条有向边)

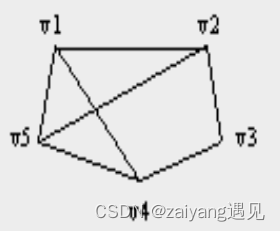
邻接表
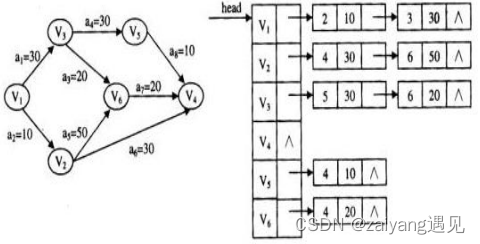
伪邻接表（链式前向星）

struct ty
{
	int dian,l;
	struct node *next;
}*[60020];
void insert(int x,int y,int z)
{
	node *p=new node;
	p->dian=y;  //x-->y
	p->l=z;  //权值
	p->next=edge[x];
	edge[x]=p;
}

struct ty{
	int t,next;
};
void insertedge(int x,int y)
{
	edge[++m].t=y;
	edge[m].next=head[x];
	head[x]=m;
}

图的DFS遍历

算法步骤：
1、从某个节点开始，每次任选一个与它相邻的未访问节点访问下去
2、直到当前节点的所有相邻节点都已经被访问过。
3、回溯到第一个未被访问过的节点

图的BFS遍历

1、用 $dis[]$ 数组表示各点距离起点 $S$ 的距离。$dis[i]=-1$ 表示 $i$ 点还未被访问。用 $map[i][j]$ 表示 $i$ 点和 $j$ 点之间是否有边。
2、将 $dis[s]$ 初始化为 $0$，将其它点的 $dis$ 初始化为 $-1$。将 $S$ 点入队
3、while（队列非空）
        从队首出队一个元素 $u$
           对于所有跟 $u$ 有边相连的点 $v$:
              if(dis[v]==-1)
                    dis[v]=dis[u]+1;
                    v入队

判断是否为欧拉图

如果图 $G$ 中的一个路径包括每个边恰好一次，则该路径称为欧拉路径(Euler path)。

如果一个回路是欧拉路径，则称为欧拉回路(Euler circuit)。

具有欧拉回路的图称为欧拉图（简称E图）。具有欧拉路径但不具有欧拉回路的图称为半欧拉图。

无向图存在欧拉回路的充要条件：
• 一个无向图存在欧拉回路，当且仅当该图所有顶点度数都为偶数,且该图是连通图。

有向图存在欧拉回路的充要条件：
• 一个有向图存在欧拉回路，所有顶点的入度等于出度且该图是连通图。

拓扑排序

一个工程常被分为多个小的子工程，这些子工程被称为活动（Activity)，在有向图中若以顶点表示活动，有向边表示活动之间的先后关系，这样的图简称为AOV网。在AOV网中为了更好地完成工程，必须满足活动之间先后关系，需要将各活动排一个先后次序即为拓扑排序。

步骤：

1. 从有向图中选取一个没有前驱的顶点，并输出之；
2. 从有向图中删去此顶点以及所有以它为尾的弧；
3. 重复上述两步，直至图空，或者图不空但找不到无前驱的顶点为止。

没有前驱 – 入度为零；删除顶点及以它为尾的弧-- 弧头顶点的入度减 $1$。

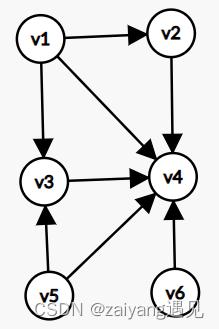
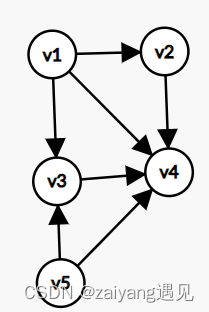
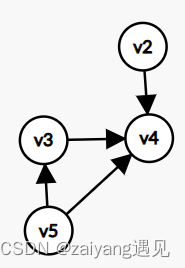
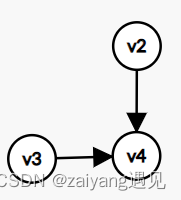
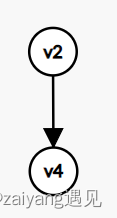
举例：
根据算法思想：
找到的点的顺序依次为 $v_6,v_1,v_5,v_3,v_2,v_4$
可以看到，拓扑排序可能有多解
(注意一边输出当前点，一边更新其他点的入度)

拓扑排序的使用：
判断一个有向图中是否有环。无环的图所有点都能进行拓扑排序。

关键路径

AOE网(Activity On Edge network)，即边表示活动的网络，与AOV网相对应，它通常表示一个工程的计划或进度。
• AOE网是一个带权的有向无环图，图中的：边：表示活动(子工程)，边上的权：表示该活动的持续时间，即完成该活动所需要的时间。
• 顶点：表示事件，每个事件是活动之间的转接点，即表示它的所有入边活动到此完成，所有出边活动从此开始。
其中有两个特殊的顶点(事件)，一个称做源点，它表示整个工程的开始，亦即最早活动的起点，显然它只有出边，没有入边；另一个称做汇点，它表示整个工程的结束，亦即最后活动的终点，显然它只有入边，没有出边。除这两个顶点外，其余顶点都既有入边，也有出边，是入边活动和出边活动的转接点。

AOE网中有些活动可以并行进行，所以完成整个工程的最短时间是从源点到汇点的最长路径长度，路径长度为路径上各边的权值之和。把从源点到汇点的最长路径长度称为关键路径。

对于一个AOE网，待研究的问题是：
(1)整个工程至少需要多长时间完成?
(2)哪些活动是影响工程进度的关键?

假设开始点是 $v_1$，从 $v_1$ 到 $v_i$ 的最长路径长度叫做事件 $v_i$ 的最早发生时间。这个时间决定了所有以 $v_i$为尾的弧所表示的活动的最早开始时间。我们用 $e(i)$ 表示活动 $a_i$ 的最早开始时间。还可以定义一个活动的最迟开始时间 $l(i)$，这是在不推迟整个工程的前提下，活动 $a_i$ 最迟必须开始进行的时间。两者之差 $l(i)-e(i)$ 意味着完成活动 $a_i$ 的时间余量。我们把 $l(i)=e(i)$ 的活动叫做关键活动。
关键路径上的所有活动都是关键活动，因此提前完成非关键活动并不能加快工程的进度。