PCA(主成分分析)降维的概念、作用及算法实现

1、PCA降维的概念

Principal Component Analysis(PCA)：主成分分析法，是最常用的线性降维方法。它的目标是通过某种线性投影，将高维的数据映射到低维的空间中表示，即把原先的n个特征用数目更少的m个特征取代，新特征是旧特征的线性组合。并期望在所投影的维度上数据的方差最大，尽量使新的m个特征互不相关。从旧特征到新特征的映射捕获数据中的固有变异性。以此使用较少的数据维度，同时保留住较多的原数据点的特性。

PCA的思想是将n维特征映射到k维上（k<n），这k维是全新的正交特征。这k维特征称为主成分，是重新构造出来的k维特征，而不是简单地从n维特征中去除其余n-k维特征。

2、PCA降维的作用

①、数据在低维下更容易处理、更容易使用；
②、相关特征容易在数据中明确的显示出来，例如：两维、三维数据，能进行可视化展示；
③、去除数据噪声
④、降低算法开销

3、PCA降维的计算步骤

下面一起通过PCA方法把二维数据降成一维来熟悉PCA降维的计算步骤。

原数据如下：

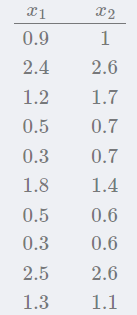
①、计算样本均值

②、用样本数据减去样本均值

运算结果如下：

③、计算数据的主成分。

矩阵的主成分是其协方差矩阵的特征向量按照对应的特征值大小排序得到的。主成分可以通过两种方法计算：第一种方法是计算数据协方差矩阵。因为协方差矩阵是方阵，所以我们可以用前面的方法计算特征值和特征向量。第二种方法是用数据矩阵的奇异值分解（singular value decomposition）来找协方差矩阵的特征向量和特征值的平方根。

上述数据集的解释变量协方差矩阵如下： 

用前面介绍过的方法，特征值是1.25057433和0.03398123，单位特征向量是：

下面我们把数据映射到主成分上。第一主成分是最大特征值对应的特征向量，因此我们要建一个转换矩阵，它的每一列都是主成分的特征向量。如果我们要把5维数据降成3维，那么我们就要用一个3维矩阵做转换矩阵。在本例中，我们将把我们的二维数据映射成一维，因此我们只需要用特征向量中的第一主成分作为转换矩阵。最后，我们用数据矩阵右乘转换矩阵。

下面就是第一主成分映射的结果： 

4、PCA降维的代码实现及结果

Python代码实现如下：

import numpy as np
x = np.mat([[ 0.9, 2.4, 1.2, 0.5, 0.3, 1.8, 0.5, 0.3, 2.5, 1.3],
            [ 1, 2.6, 1.7, 0.7, 0.7, 1.4, 0.6, 0.6, 2.6, 1.1]])
x = x.T
T = x - x.mean(axis=0)
C = np.cov(x.T)
w,v = np.linalg.eig(C)
v_ = np.mat(v[:,0])     #每个特征值对应的是特征矩阵的每个列向量
v_ = v_.T               #默认以行向量保存，转换成公式中的列向量形式
y = T * v_
print(y)

运行结果如下：

5、参考资料：

https://www.imooc.com/article/44218

https://blog.csdn.net/HLBoy_happy/article/details/77146012