A Survey on Concept Drift Adaptation Note

A Survey on Concept Drift Adaptation

Abstract

Concept drift primarily refers to an online supervised learning scenario when the relation between the input data and the target variable changes over time. Assuming a general knowledge of supervised learning in this article, we characterize adaptive learning processes; categorize existing strategies for handling concept drift; overview the most representative, distinct, and popular techniques and algorithms; discuss evaluation methodology of adaptive algorithms; and present a set of illustrative applications. The survey covers the different facets of concept drift in an integrated way to reflect on the existing scattered state of the art. Thus, it aims at providing a comprehensive introduction to the concept drift adaptation for researchers, industry analysts, and practitioners.

当输入数据和目标变量之间的关系随时间变化时，概念漂移主要是指在线监督学习场景。 假设本文具有监督学习的一般知识，我们将描述自适应学习过程的特征。 对处理概念漂移的现有策略进行分类； 概述最具代表性，独特和流行的技术和算法； 讨论自适应算法的评估方法； 并展示了一组说明性应用。 这项调查以综合的方式涵盖了概念漂移的不同方面，以反思现有的现有分散状态。 因此，它旨在为研究人员，行业分析人员和从业人员全面介绍概念漂移适应。

Introduction

However, very often data comes in the form of streams. Accommodating large volumes of streaming data in the machine’s main memory is impractical and often infeasible. Hence, only an online processing is suitable. In this case, predictive models can be trained either incrementally by continuous update or by retraining using recent batches of data. But computational efficiency is not the only issue in supervising learning from data steams.

但是，数据经常以流的形式出现。 在机器的主内存中容纳大量流数据是不切实际的，而且通常是不可行的。 因此，仅在线处理是合适的。 在这种情况下，可以通过连续更新或通过使用最近一批数据进行重新训练来增量地训练预测模型。 但是，计算效率并不是监督数据流学习的唯一问题。

In dynamically changing and nonstationary environments, the data distribution can change over time, yielding the phenomenon of concept drift [Schlimmer and Granger 1986; Widmer and Kubat 1996]. The real concept drift1 refers to changes in the condi- tional distribution of the output (i.e., target variable) given the input (input features), while the distribution of the input may stay unchanged. A typical example of the real concept drift is a change in users’ interests when following an online news stream. While the distribution of the incoming news documents often remains the same, the conditional distribution of the interesting (and thus not interesting) news documents for that user changes. Adaptive learning refers to updating predictive models online during their operation to react to concept drifts.

在动态变化和非平稳的环境中，数据分布会随着时间而变化，从而产生概念漂移现象[Schlimmer and Granger 1986; Widmer and Kubat 1996]。 实际概念漂移1是指在给定输入（输入要素）的情况下，输出（即目标变量）的有条件分布的变化，而输入的分布可能保持不变。 真实概念漂移的一个典型示例是关注在线新闻流时用户兴趣的变化。 尽管传入新闻文档的分发通常保持不变，但该用户感兴趣（因此不感兴趣）的新闻文档的条件分发会发生变化。 自适应学习是指在预测模型运行过程中在线更新它们以对概念漂移做出反应。

The present contribution provides an integrated view on handling concept drift by surveying adaptive learning methods, presenting evaluation methodologies, and dis- cussing illustrative applications. It focuses on online supervised learning when the relation between the input features and the target variable changes over time.

本文稿通过调查自适应学习方法，介绍评估方法并讨论说明性应用，提供了有关处理概念漂移的综合视图。 当输入要素和目标变量之间的关系随时间变化时，它专注于在线监督学习。

Adaptive Learning Algorithms

Learning algorithms often need to operate in dynamic environments, which are chang- ing unexpectedly. One desirable property of these algorithms is their ability of incor- porating new data. If the data-generating process is not strictly stationary (as applies to most of the real-world applications), the underlying concept, which we are predict- ing (e.g., interests of a user reading news), may be changing over time. The ability to adapt to such concept drift can be seen as a natural extension for the incremental learning systems [Giraud-Carrier 2000] that learn predictive models example by ex- ample. Adaptive learning algorithms can be seen as advanced incremental learning algorithms that are able to adapt to evolution of the data-generating process over time.

学习算法通常需要在意想不到的动态环境中运行。 这些算法的一个理想特性是其合并新数据的能力。 如果数据生成过程不是严格固定的（适用于大多数现实应用程序），那么我们正在预测的基本概念（例如，用户阅读新闻的兴趣）可能会随着时间而改变。 适应这种概念漂移的能力可以看作是增量学习系统的自然扩展[Giraud-Carrier 2000]，该系统通过示例来学习预测模型。 自适应学习算法可以看作是高级增量学习算法，能够随着时间的推移适应数据生成过程的发展。

Setting and Definitions

In contrast, online algorithms process data sequentially. They produce a model and put it in operation without having the complete training dataset available at the beginning. The model is continuously updated during operation as more training data arrives.

相反，在线算法按顺序处理数据。 他们生成了一个模型并将其投入运行，而一开始没有完整的训练数据集。 随着更多训练数据的到来，该模型会在操作过程中不断更新。

Less restrictive than online algorithms are incremental algorithms that process input examples one by one (or batch by batch) and update the decision model after receiving each example. Incremental algorithms may have random access to previous examples or representative/selected examples. In such a case, these algorithms are called in- cremental algorithms with partial memory [Maloof and Michalski 2004]. Typically, in incremental algorithms, for any new presentation of data, the update operation of the model is based on the previous one.

与在线算法相比，限制性更强的算法是增量算法，该算法逐个处理输入示例（或逐批处理），并在收到每个示例后更新决策模型。 增量算法可以随机访问先前的示例或代表性/精选示例。 在这种情况下，这些算法称为带有部分内存的增量算法[Maloof和Michalski 2004]。 通常，在增量算法中，对于任何新的数据表示形式，模型的更新操作均基于前一个模型。

Because data is expected to evolve over time, especially in dynamically changing environments, where nonstationarity is typical, its underlying distribution can change dynamically over time. The general assumption in the concept drift setting is that the change happens unexpectedly and is unpredictable, although in some particular real-world situations, the change can be known ahead of time in correlation with the occurrence of particular environmental events. But solutions for the general case of drift entail the solutions for the particular cases. Moreover, the change may take different forms (i.e., the input data characteristics or the relation between the input data and the target variable may change).

因为预计数据会随着时间的推移而发展，尤其是在动态变化的环境（通常是非平稳性）中，所以其基本分布会随着时间动态变化。 概念漂移设置中的一般假设是，更改会意外发生且不可预测，尽管在某些特定的实际情况下，可以与特定环境事件的发生相关地提前知道更改。 但是，针对一般漂移的解决方案需要针对特定情况的解决方案。 而且，改变可以采取不同的形式（即，输入数据特性或输入数据与目标变量之间的关系可以改变）。

Formally, concept drift between time point t0 and time point t1 can be defined as

where denotes the joint distribution at time t0 between the set of input variables X and the target variable y. Changes in data can be characterized as changes in the components of this relation [Kelly et al. 1999; Gao et al. 2007]. In other terms:

—the prior probabilities of classes p(y) may change,
—the class conditional probabilities p(X|y) may change, and
—as a result, the posterior probabilities of classes p(y|X) may change, affecting the

prediction.

We are interested to know two implications of these changes: (i) whether the data distribution p(y|X) changes and affects the predictive decision and (ii) whether the changes are visible from the data distribution without knowing the true labels (i.e., p( X) changes). From a predictive perspective, only the changes that affect the prediction decision require adaptation.

We can distinguish two types of drifts:

(1) Real concept drift refers to changes in p(y|X). Such changes can happen either with or without change in p(X). Real concept drift has been referred to as concept shift in Salganicoff [1997] and conditional change in Gao et al. [2007].

(2) Virtual drift happens if the distribution of the incoming data changes (i.e., p(X) changes) without affecting p(y|X) [Delany et al. 2005; Tsymbal 2004; Widmer and Kubat 1993]. However, virtual drift has had different interpretations in the literature:

—Originally, a virtual drift was defined [Widmer and Kubat 1993] to occur due to incomplete data representation rather than change in concepts in reality.

—Virtual drift corresponds to change in data distribution that leads to changes in the decision boundary [Tsymbal 2004].

—Virtual drift is a drift that does not affect the target concept [Delany et al. 2005].

形式上，时间点t0和时间点t1之间的概念漂移可以定义为∃X：pt0（X，y）̸= pt1（X，y），（2）其中pt0表示在时间t0时，一组之间的联合分布。 输入变量X和目标变量y。 数据的变化可以被描述为这种关系的组成部分的变化[Kelly等。 1999年； 高等。 2007]。 换句话说：-类p（y）的先验概率可能会发生变化；-类条件条件概率p（X | y）可能会发生变化；以及-结果，类p（y | X）的后验概率可能会发生变化 ，影响预测。
我们有兴趣知道这些变化的两个含义：（i）数据分布p（y | X）是否发生变化并影响预测决策；（ii）在不知道真实标签的情况下，数据更改是否可见于数据分布（即 ，p（X）变化）。 从预测的角度来看，只有影响预测决策的更改才需要调整。
我们可以区分两种类型的漂移：（1）实际概念漂移是指p（y | X）的变化。 无论p（X）有无变化，这种变化都可能发生。 实际的概念漂移在Salganicoff [1997]中被称为概念漂移，在Gao等人中被称为条件变化。 [2007]。
（2）如果传入数据的分布发生变化（即p（X）发生变化）而又不影响p（y | X），则会发生虚拟漂移[Delany等。 2005; Tsymbal 2004； Widmer and Kubat 1993]。 但是，虚拟漂移在文献中有不同的解释：—最初，虚拟漂移被定义为[Widmer and Kubat 1993]是由于数据表示不完整而不是实际概念的改变而发生的。
-虚拟漂移对应于导致决策边界发生变化的数据分布变化[Tsymbal 2004]。
虚拟漂移是一种不影响目标概念的漂移[Delany等。 2005]。

This survey primarily focuses on handling the real concept drift, which is not visible from the input data distribution. In many cases, the techniques that handle the real concept drift can also handle drifts that manifest in the input data distributions, but not the other way around. Techniques for handling the real concept drift typically rely on feedback about the predictive performance, while techniques for tracking changing prior probabilities and techniques for handling virtual drift or novelty detection typi- cally can operate without such feedback. This article does not cover such drifts that can be detected from the incoming data distribution (P(X)). Readers interested in tracking drifting prior probabilities are referred to Zhang and Zhou [2010], in novelty detection are referred to Markou and Singh [2003] and Masud et al. [2011], and in handling virtual drifts by semisupervised learning techniques using on clustering are referred to Aggarwal [2005], Bouchachia et al. [2010], and Bouchachia and Vanaret [2013].

该调查主要集中于处理实际概念漂移，这在输入数据分布中是不可见的。 在许多情况下，处理实际概念漂移的技术还可以处理在输入数据分布中表现出来的漂移，但反之则不行。 处理真实概念漂移的技术通常依赖于有关预测性能的反馈，而用于跟踪变化的先验概率的技术和用于处理虚拟漂移或新颖性检测的技术通常可以在没有此类反馈的情况下运行。 本文没有涵盖可以从传入数据分布（P（X））中检测到的漂移。 有兴趣追踪漂移先验概率的读者请参见Zhang和Zhou [2010]，新颖性检测请参见Markou和Singh [2003]和Masud等。 [2011]，以及在使用基于聚类的半监督学习技术处理虚拟漂移时，请参考Aggarwal [2005]，Bouchachia等。 [2010]，以及Bouchachia和Vanaret [2013]。

Changes in Data Over Time

Changes in data distribution over time may manifest in different forms, as illustrated in Figure 2 on a toy one-dimensional data. In this data, changes happen in the data mean. A drift may happen suddenly/abruptly, by switching from one concept to another (e.g., replacement of a sensor with another sensor that has a different calibration in a chemical plant), or incrementally, consisting of many intermediate concepts in between(e.g., a sensor slowly wears off and becomes less accurate). Drift may happen suddenly (e.g., the topics of interest that one is surveying as a credit analyst may suddenly switch from, for instance, meat prices to public transportation) or gradually (e.g., relevant news topics change from dwelling to holiday homes, while the user does not switch abruptly, but rather keeps going back to the previous interest for some time). One of the challenges for concept drift handling algorithms is not to mix the true drift with an outlier or noise, which refers to a once-off random deviation or anomaly (see Chandola et al. [2009] for outlier detection). No adaptivity is needed in the latter case. Finally, drifts may introduce new concepts that were not seen before, or previously seen concepts may reoccur after some time (e.g., in fashion). Changes can be further characterized by severity, predictability, and frequency [Minku et al. 2010; Kosina et al. 2010].

Most of the adaptive learning techniques implicitly or explicitly assume and spe- cialize in some subset of concept drifts. Many of them assume sudden nonreoccurring drifts. But in reality, often mixtures of many types can be observed.

数据分布随时间的变化可能以不同的形式体现出来，如图2所示的玩具一维数据。 在此数据中，数据均值发生变化。 漂移可能会突然/突然发生，方法是从一个概念切换到另一个概念（例如，用化工厂中标定不同的另一个传感器替换传感器），也可能是渐进式的，包括介于两者之间的许多中间概念（例如，传感器缓慢磨损并变得不那么精确）。 漂移可能突然发生（例如，作为信用分析员正在调查的感兴趣的主题可能突然从例如肉类价格转变为公共交通）或逐渐发生（例如，相关新闻主题从住宅变为度假屋，而 用户不会突然切换，而是会在一段时间内回到先前的兴趣）。 概念漂移处理算法的挑战之一是不要将真正的漂移与离群值或噪声混合在一起，后者是指一次性的随机偏差或异常（离群值检测请参见Chandola等人[2009]）。 在后一种情况下，不需要适应性。 最后，漂移可能会引入以前未见过的新概念，或者一段时间后（例如，以时尚的形式）可能会再次出现以前见过的概念。 变化可以通过严重性，可预测性和频率来进一步表征[Minku et al。 2010; Kosina等。 2010]。
大多数适应性学习技术都隐含或显式地假定并特定化了概念漂移的某些子集。 他们中的许多人都假设突然发生了不可重复的漂移。 但实际上，通常可以观察到多种类型的混合物。

• Sudden / abrupt: 指的是迅速同时又不可逆的改变， 强调的是发生迅速
• Incremental：增量改变，强调的是改变发生缓慢， 强调的是值随时间发生改变
• gradual：循序渐进改变，强调的是数据分布的改变
• reccuring：是一种temporary（临时性）的改变，在一段时间内会回复之前的状态。所以也有些研究者将其称为loacl drift，它不具有周期性，是在不规则的时间间隔内反复转换。
• outlier：离群值，是一种随机变化

以上是根据变化速度进行划分的概念漂移。

Requirements for Predictive Models in Changing Environments(不断变化的环境对预测模型的要求)

Predictive models that operate in these settings need to have mechanisms to detect and adapt to evolving data over time; otherwise, their accuracy will degrade. As time passes, the decision model may need to be updated taking into account the new data or be completely replaced to meet the changed situation. Predictive models are required to:

1. detect concept drift (and adapt if needed) as soon as possible;

2. distinguish drifts from noise and be adaptive to changes, but robust to noise; and

3. operate in less than example arrival time and use not more than a fixed amount of memory for any storage.

在这些情况下运行的预测模型需要具有机制，可以随着时间的推移检测和适应不断发展的数据。 否则，它们的准确性将会降低。 随着时间的流逝，可能需要考虑新数据来更新决策模型，或者完全替换决策模型以满足变化的情况。 需要预测模型以：（1）尽快检测概念漂移（并在需要时进行调整）； （2）区分漂移和噪声，并能适应变化，但对噪声具有鲁棒性； （3）在少于示例到达时间的情况下运行，并且任何存储使用不超过固定数量的内存。

Online Adaptive Learning Procedure(在线适应算法程序）

在线自适应学习的正式定义如下。 决策模型是将输入变量映射到目标的函数L：y = L（X）。 学习算法指定了如何从一组数据实例构建模型。
在线自适应学习程序如下：（1）预测。 当新的示例X到达时，使用当前tt（2）诊断做出预测yˆ。 一段时间后，我们会收到真实的标签yt，并且可以估算损失模型Lt. a s f（yˆ，y）。
tt（3）更新。 我们可以使用示例（Xt，yt）进行模型更新以获得Lt + 1。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-F9nXLbIm-1607226885465)(/Users/liyan/Library/Application Support/typora-user-images/image-20201130160952655.png)]

取决于计算资源，使用模型的最新版本Lt + 1 = train（（Xt，yt），Lt）处理后，可能需要丢弃数据。 或者，某些过去的数据可能仍可访问Lt + 1 = train（（Xi，yi），…，（Xt，yt），Lt）。 有多种在线处理数据的方式（例如，部分内存：一些示例在培训中定期存储和使用;基于窗口的数据以块的形式显示;基于实例的示例在到达时进行处理）。

Figure 3 depicts a generic schema for an online adaptive learning algorithm. In a nutshell, the memory module defines how and which data is presented to the learning algorithm (learning module). The loss estimation module tracks the performance of the learning algorithm and sends information to the change detection module to update the model if necessary. Section 3 will discuss the four modules of the system (memory, learning, change detection, loss estimation) in detail.

This setting has variations where, for instance, the true values for the target vari- able (feedback) come with a delay or are not available at all. Moreover, new examples for prediction may arrive before we get feedback for the data that has already been processed. In such a case, model update would be delayed, but the principles of oper- ation remain the same. Finally, in some settings, we may need to process examples in batches rather than one by one.

图3描绘了在线自适应学习算法的通用架构。 简而言之，存储模块定义了如何将数据以及哪些数据呈现给学习算法（学习模块）。 损失估计模块跟踪学习算法的性能，并在必要时将信息发送到更改检测模块以更新模型。 第三部分将详细讨论系统的四个模块（内存，学习，更改检测，损失估计）。
此设置有一些变化，例如，目标变量（反馈）的真实值会延迟或根本不可用。 此外，在我们获得对已处理数据的反馈之前，可能会出现新的预测示例。 在这种情况下，模型更新将被延迟，但是操作原理保持不变。 最后，在某些情况下，我们可能需要分批处理示例，而不是一个接一个地处理示例。

TAXONOMY OF METHODS FOR CONCEPT DRIFT ADAPTATION

Memory

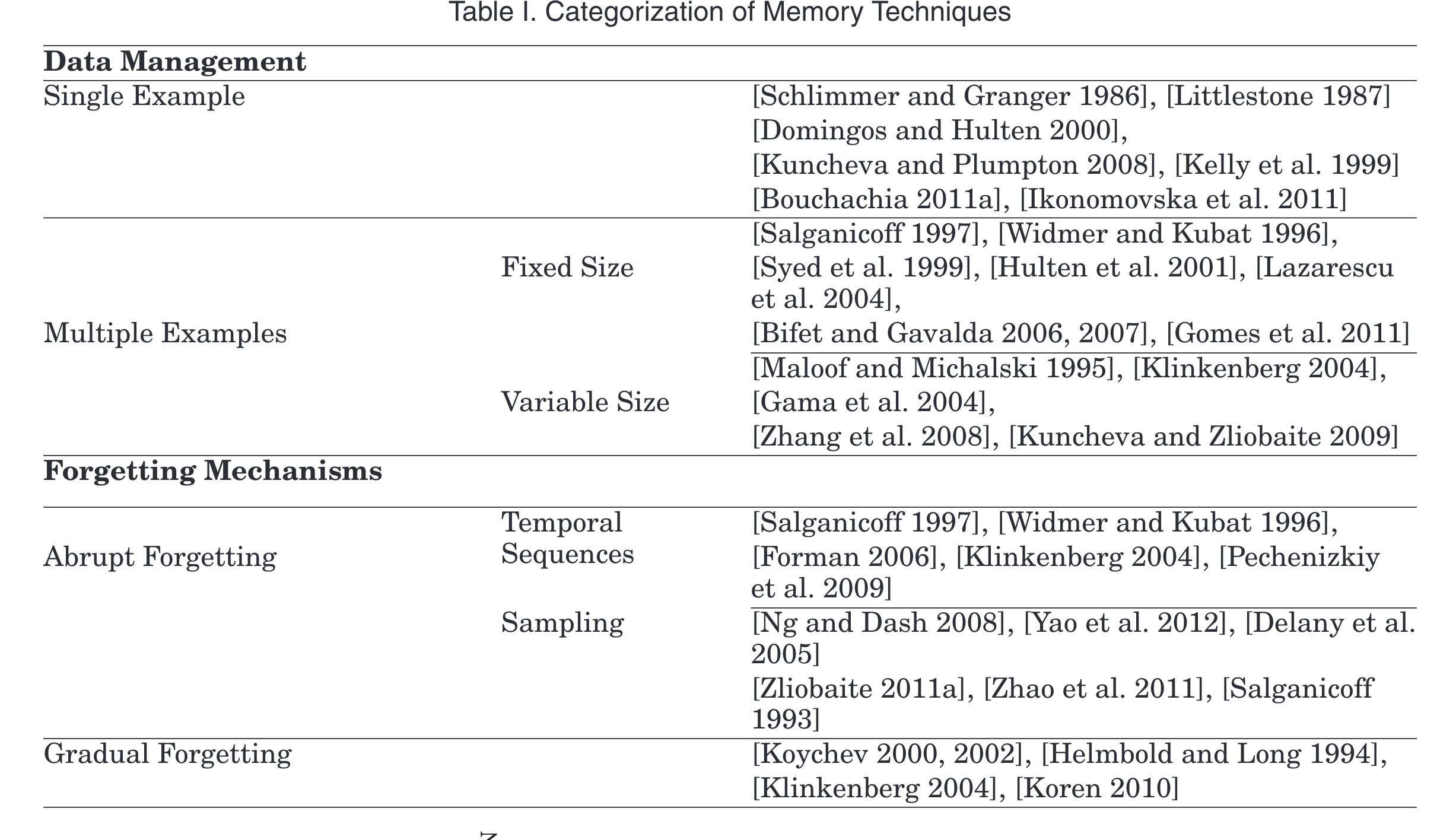
Learning under concept drift requires not only updating the predictive model withnew information but also forgetting the old information. We consider two types ofmemory: short-term memory represented as data and long-term memory representedas generalization of data models. In this subsection, we analyze the short-term memoryunder two dimensions as illustrated in Figure 5: (i)data managementspecifies whichdata is used for learning, and (ii)forgetting mechanismspecifies in which way old datais discarded. The issues of long-term memory will be discussed in Section 3.3

概念漂移下的学习不仅需要用新的信息更新预测模型，而且需要遗忘旧的信息。我们考虑两种类型的内存：以数据表示的短期内存和作为数据模型泛化的长期内存。在本小节中，我们从两个维度分析短期内存，如图5所示：（i）数据管理指定用于学习的数据，以及（ii）遗忘机制指定以何种方式丢弃旧数据。长期记忆的问题将在3.3节.

Data Management

数据管理学习最新的数据，并且最新的数据量对当前的预测影响最大

Single Examples

Most online learners maintain a single hypothesis (which can originate froma complex predictive model) and model updates are error driven. When a new exampleXtarrives, a prediction ˆytis made by the current hypothesis. When the true target valueytis received, loss is computed and the current hypothesis is updated if necessary. Anexample of such algorithms isWINNOW[Littlestone 1987], which is a linear classifiersystem that uses a multiplicative weight-update scheme. The key characteristic ofWINNOWis its robustness to irrelevant features.

大多数在线学习者维持一个单一的假设（可能来自一个复杂的预测模型），模型更新是错误驱动的。当一个新的例子出现时，根据当前的假设做出一个预测。当收到真实的目标值时，计算损失，必要时更新当前假设。这类算法的一个例子是winnow[Littlestone 1987]，这是一个使用乘法权重更新方案的线性分类器系统。它的关键特征是对无关特征的鲁棒性。

Online learning algorithms can be seen as naturally adaptive to evolving distribu-tions, mainly due to their learning mechanisms that continuously update the model with the most recent examples. However, online learning systems do not have explicitforgetting mechanisms. Adaptation happens only as the old concepts are diluted due tothe new incoming data. Systems likeWINNOW[Littlestone 1987] andVFDT[Domingos andHulten 2000] can adapt to slow changes over time. The main limitation is their slowadaptation to abrupt changes, which depends on how sensible the model update with anew example is set to be. Setting these parameters requires a tradeoff between stabilityand sensitivity [Carpenter et al. 1991b]. Representativesingle instance memorysys-tems that explicitly deal with concept drift includeSTAGGER[Schlimmer and Granger1986],DWM[Kolter and Maloof 2003, 2007],SVM[Syed et al. 1999],IFCS[Bouchachia2011a], andGT2FC[Bouchachia and Vanaret 2013]

在线学习算法可以被视为自然地适应不断变化的分布，主要是因为它们的学习机制不断地用最新的例子更新模型。然而，在线学习系统没有明确的预测机制。只有当旧概念因新的输入数据而被稀释时，才会发生适应。像winnow[Littlestone 1987]和vfdt[Domingos and hulten 2000]这样的系统可以适应随着时间的推移而缓慢的变化。主要的局限性是它们对突变的适应能力慢，这取决于用新的例子进行模型更新的合理性。设置这些参数需要在稳定性和灵敏度之间进行权衡【Carpenter等人，1991b】。明确处理概念漂移的代表性单实例记忆系统项目包括Tagger[Schlimmer and Granger1986]、DWM[Kolter and Maloof 2003，2007]、SVM[Syed et al.1999]、IFCS[Bouchachia2011a]和GT2FC[Bouchachia and Vanaret 2013]

Multiple Examples

Another approach to data management is to maintain a pre-dictive model consistent with a set of recent examples. The algorithm familyFLORA[Widmer and Kubat 1996] is one of the first supervised incremental learning systemsfor evolving data. The originalFLORAalgorithm uses a sliding window of a fixed length,which stores the most recent examples in thefirst-in-first-out (FIFO)data structure.At each time step, the learning algorithm builds a new model using the examples fromthe training window. The model is updated following two processes: a learning process(update the model based on the new data) and a forgetting process (discard data thatis moving out of the window). The key challenge is to select an appropriate windowsize. A short window reflects the current distribution more accurately; thus, it canensure fast adaptation in times with concept changes, but during stable periods, a tooshort window worsens the performance of the system. A large window gives a betterperformance in stable periods, but it reacts to concept changes more slowly.In general, the training window size can befixedorvariableover time.

数据管理的另一种方法是维护一个预测模型，该模型与最近的一组示例保持一致。familyFLORA算法[Widmer and Kubat 1996]是第一个针对进化数据的有监督增量学习系统之一。原始floral算法使用固定长度的滑动窗口，将最新的示例存储在先进先出（FIFO）数据中结构。At每一个时间步，学习算法都会使用训练窗口中的例子建立一个新的模型。模型的更新有两个过程：学习过程（基于新数据更新模型）和遗忘过程（丢弃窗口外的数据）。关键的挑战是选择合适的窗口大小。短窗口更准确地反映了当前的分布，因此，它不能保证在概念变化的时间内快速适应，但在稳定时期，过短窗口会使系统的性能恶化。一个大窗口在稳定时期会有更好的表现，但它对概念变化的反应更大慢慢地。进来一般来说，训练窗口的大小可以随时间变化.

Sliding windows of a fixed size.Store in memory a fixed number of the most recentexamples. Whenever a new example arrives, it is saved to memory and the oldestone is discarded. This simple adaptive learning method is often used as a baselinein evaluation of new algorithms.Sliding windows of variable size.

固定式滑动窗大小。存储内存中固定数量的最新实例。每当一个新的例子出现时，它被保存到内存中，旧的语句被丢弃。这种简单的自适应学习方法经常被用作评估新的算法。

Vary the number of examples in a window overtime, typically depending on the indications of a change detector. A straightforwardapproach is to shrink the window whenever a change is singled such that the trainingdata reflects the most recent concept and grow the window otherwise

根据变化检测器的指示，在窗口超时时改变示例的数量。一种直接的方法是在每次选中一个更改时缩小窗口，这样trainingdata就可以反映最新的概念，否则就扩大窗口。

One of the first algorithms using an adaptive window size was theFLORA2[Widmerand Kubat 1996]. Incoming examples are added to the window and the oldest onesare deleted. Addition and deletion keep the window (and the predictive model) consis-tent with the current concept. Further versions of the algorithm deal with recurringconcepts (FLORA3) and noisy data (FLORA4). A later study [Klinkenberg and Joachims2000] presents a theoretically supported method for re