度与弧度

度与弧度

1.度

度，即我（一名观察者）转动多少角度才能够看到你（移动对象）。有点自我为中心，你不觉得是吗？

自私，是吗？这就是我们如何对待数学的态度。我们根据“我需要转动多少角度才能看到那个星球、钟摆、亦或是车轮的移动”，来构建数学公式。但是，你从来没有站在另外一个角度看待这些事物。

2.弧度

弧度，并不是那么自私的选择。许多物理现象（生活中）常常是脱离了自我为中心的角度，从另外一种不那么自私的角度看待事物。因此，与其从我的头部需要转动多少角度看到移动对象的观察角度来描述对象，倒不如从移动对象移动多少距离来描述对象。

度测量角度是依据我需要转动多少度才能够看到物体对象；弧度测量角度是一句物体对象移动的距离。

但是，对于弧度来说，绝对距离并不是十分有效。因为，移动的距离是10米，对于不同轨迹（不同的半径）来说是不同的数字。半径为1移动10米和半径为2移动10米的距离，弧度所表示的值是不一样的。因此，我们除以轨迹的半径获得一个归一化的角度：

所以，在一些文献中常常看到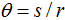，或者是以弧度为单位的角度=弧长除以对应的半径。

一个圆一圈又360度或者说是弧度2*Pi，所以1弧度大概与等于57.3度。移动1弧度（单位）就是移动了一个完美的归一化距离。话句话说，就是移动90度，意味着移动对象移动了个Pi/2弧度单位。

弧度在数学处理中作用很大。弧度让我们从以我为中心的角度转换到以移动对象的角度看待事物。度和弧度，只是看待事物的不同角度而已，描述都是同一个物体对象。在某些场景下，我们从物体对象的角度出发，往往能够很好的解决问题。

严格说来，弧度只是一个比例，我们可以这么理解弧度，即物体在单位圆上移动的距离。

3.使用弧度

例1：

假设有一辆轮胎半径为2米的巴士（是一辆巨型巴士）。我将告知从轮胎转动的速度，而你将告诉巴士移动的速度？准备好呢？

以观察者的角度计算这辆巴士所移动的速度。

“这辆巴士每秒轮胎转动2000度”，之后你会这么计算：

1.      OK。轮胎每秒转动2000度。意味着每一秒转动2000/360圈，即5又5/9圈每秒。一圈的长度是。所以，巴士移动总的距离是2乘以3.14乘以5又5/9……，我的计算器在哪？

以观察对象的角度计算巴士移动的速度。

“轮胎每秒钟转动6弧度”，你会这样想：

弧度是在单位圆上移动的距离。那么，半径为2的圆，其移动的距离应该是6*2=12米每秒。

喔！没有复杂的公式，没有Pi，我们只是把转动速度（角速度）转换为线速度。这么简单的计算出结果，只是因为我们从观察对象的角度看待问题。

例2：

Sin（x）

x以度为单位，在计算器总输入sin(x)。当你输入的x越小，比如说0.1，sin(x)也是比较小的。Sin(x)/x的比值大概是0.017。这意味着什么呢？乘以或除以一个度为单位的值表示什么含义呢？你能够对度开平方或是对其求立方？

这个时候我们能够从弧度考虑上述问题，那么将迎刃而解。我们可以把上述比例解释为：

1.        X在单位圆上你所移动的距离

2.        Sini(x)即在单位圆上你所在的高度

所以，sin(x)/x的比值意味着你在单位圆上的高度除以在单位圆上移动的距离。如果你垂直移动，那么sinx/x的比例为100%，若果水平移动，其比例为0%。

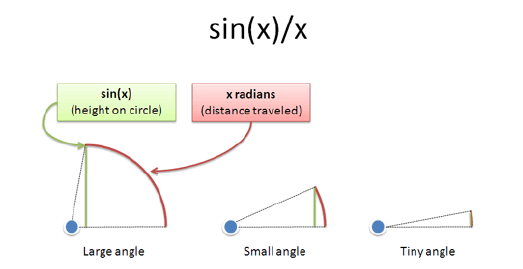
如果物体移动范围很小，从我们的角度来看，比如0或者是1度。基本上来说是直接向上运动。如果移动的更小的范围，比如0到0.00001度。那么可以直接说是垂直运动了。物体移动的而距离x将与物体的高度很接近。这也就是为什么当x很小的时候，sinx/x其比值接近为1。

虽然我们可以通过计算得出上述的关系，但是弧度能够很好的帮助我们理解为什么会是这样的结果。上述关系只有以弧度为单位才成立。

参考文献：

Math Better Explained

知乎的一个问答： 弧度是怎么来的？为什么要用弧度？起源是什么？