单摆测定重力加速度

西 南 石 油 大 学 实 验 报 告

课  程	物理实验	实验项目	单摆测定重力加速度	成  绩
专业班级		学  号		指导教师
姓  名		实验日期

• 实验目的：

1、掌握单摆测重力加速度的基本原理

2、掌握作图法或最小二乘法

3、分析摆长和摆角对测量结果的影响

4、熟悉Phyphox、Tracker等相应软件的使用

（二）实验内容：

1、根据相对不确定度不大于5%的要求确定摆长和测量的周期数。

2、测量小角度摆动下单摆的周期（要求用Tracker、Phyphox等软件进行测量）。

3、利用作图法或最小二乘法，根据T2-L关系计算重力加速度，并分析其不确定度。

查阅实验所在地重力加速度，计算百分误差，分析误差原因。

4、研究不同摆长或不同摆角对实验结果的影响。摆长和摆角同学们可以只选择一个进行研究，每种情况至少研究3个及以上变化值，得出结论并简要叙述规律。

（三）实验原理：

1. 摆角，忽略摆球形状、摆球质量、空气影响时的周期:

当偏角很小的时候，单摆做简谐运动，有由公式T=2πLg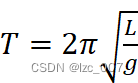    可得重力加速度g =4π2LT2 

              T=2πLg                 

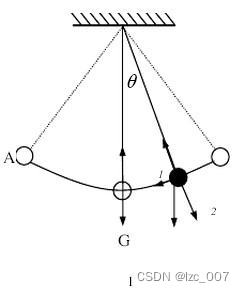
图1 单摆示意图

2、大摆角，忽略摆球形状和质量、空气影响时的周期：

T=2πLg1+14sin2θm2+⋯     

（四）实验设备：

轻质细绳、装有phyphox的手机、刻度尺。

（五）实验步骤：

1、将细绳一端固定在竖直墙面上，另一端固定在手机上，让手机面与墙面平

行，做成一个摆。

2、打开phyphox软件，下拉菜单找到“力”下的“摆”，让手机偏离平衡位置-一个小角度，点击运行按钮，放手后，软件会根据陀螺仪测量的数据自动记录单摆的周期和频率。

3、利用作图法或最小二乘法，根据T2-L关系计算重力加速度，并分析其不确定度。

4、查阅成都的重力加速度，计算百分误差。

5、改变角度的大小即改变单摆的周期，按照如上步骤多次进行测量，并记录

数据。

（六）注意事项：

1、摆动时摆角不宜过大；

2、摆线要细而且无弹性，悬点要固定；

3、单摆要在竖直平面内移动，不能形成锥摆；

4、测摆长在单摆竖直悬挂状态；

5、测单摆周期时，在摆球经过平衡位置时开始计数。

（七）实验数据记录与处理：

1、数据表格：

序号	1	2	3	4	5
周期T（s）	1.52	1.49	1.50	1.51	1.53
T2	2.31	2.22	2.25	2.28	2.34
摆长L（cm）	55.6
重力加速度g（m/s2）	9.50	9.86	9.72	9.63	9.38

经查阅，成都的重力加速度为9.7913。

2、数据处理：

1）对于周期T：

周期T的平均值：T=1ni=1nTi=1.51s；

A类不确定度：UCT=i=1n(Ti-T)2n(n-1)=i=15(Ti-1.51)25×4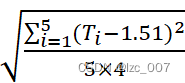≈0.08;

B类不确定度：UBT=i=1k(△xmi(T)3)2=(0.013)2≈0.006;

周期T的标准不确定度：UCT=UA2T+UB2(T)=(0.08)2+(0.006)2≈0.09;

所以周期T=T+UCT=1.51±0.09  （s）

2）对于重力加速度g的不确定度分析：

根据公式g =4π2LT2；

间接测量量g的平均值：g=1ni=1ngi=9.618≈9.6 ms2;

间接测量量g的标准不确定度为：UCg=∂f∂LUL2=0.67≈0.7

故重力加速度g=9.6±0.7（ms2）；

（八）结论及结果的分析讨论（实验误差分析）

1、结论及结果：

1）通过正常的实验流程并通过公式计算得到的g=9.6±0.7（ms2），而通过上网查询的成都本地的重力加速度为9.7913（ms2）。

百分误差约为19.54%；

2）改变单摆的摆角，经过测量和计算，单摆的周期会随着其摆角的改变而改变；当摆角小于5度时，摆球到达最低点的速度较小，空气阻力较小，满足相关公式，得出的重力加速度误差较小；当摆角较大时，速度较大，空气阻力不能忽略，得出的结果误差较大。

2、误差分析：

1）毫米刻度尺的精度引起的误差；

2）将细线缠绕手机的方案代替用细线连接小球，小球的质心在其几何中心，而手机的质心很难确定，整个系统的质心上移，导致L测>L实，其中L测指测量得到的L，L实指细线末端到手机质心的距离；

3）将细线缠绕手机，必定在细线和手机的连接处产生空隙，使用刻度尺在这测量的误差进一步加大；

4）由于手机的质量分布不像小球那样均匀，体积也并非球形，其产生的空气阻力不可忽略不计；

5）其余因为不熟悉操作流程导致操作失误的偶然误差。